二叉树的前、中、后序遍历（递归方法 + 非递归方法）

树结构

二叉树

为什么需要树这种数据结构

数组存储方式的分析

优点： 通过下标方式访问元素，速度快。对于有序数组，还可使用二分查找提高检索速度！

缺点： 如果检索某个具体值时，或者插入值（按一定顺序）会整体移动，效率较低

链式存储方式的分析

优点： 在一定程度上对数组存储方式有优化（比如：插入一个数值节点，只需要将插入的节点链接到链表中即可，删除节点效率也很好）!

缺点： 在进行检索时，效率较低，比如（检索某个值时，需要从头节点开始遍历）！

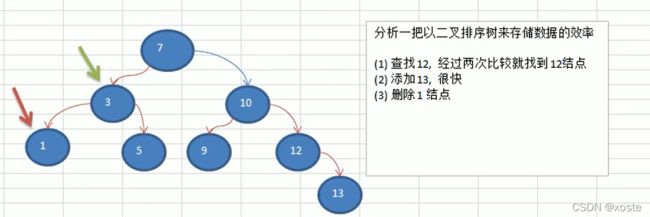
树存储方式的分析

能提高数据存储，读取的效率，比如利用 二叉排序树（Binary Sort Tree），既可以保证数据的检索速度，同时也可以保证数据的插入，删除，修改的速度！

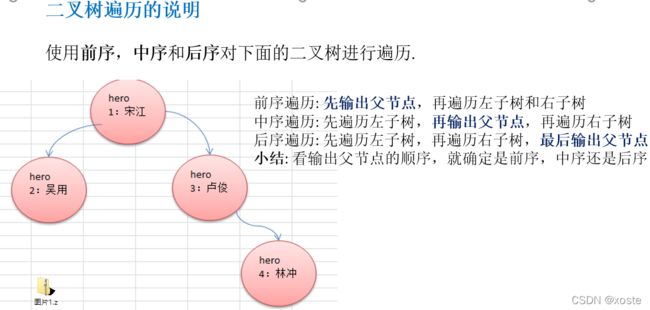
前序、中序、后序遍历

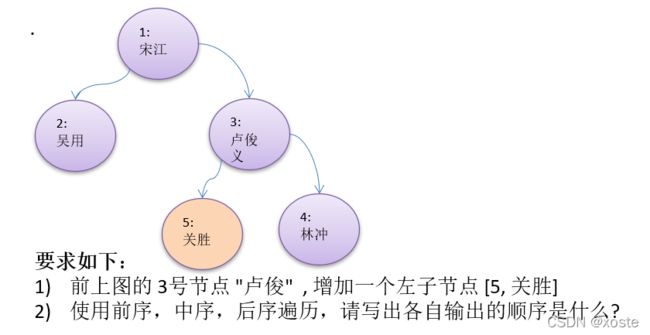
例图

代码

package com.xoste.datastructure.binarytree;

import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.Stack;

/**
 * @author xoste
 * @date 2022/4/19 14:32
 */
public class BinaryTree {

    private HeroNode root;

    public HeroNode getRoot() {
        return root;
    }

    public void setRoot(HeroNode root) {
        this.root = root;
    }

    /**
     * 递归方法
     * 前序遍历
     */
    public void preorder() {
        if (this.root != null) {
            this.root.preorder();
        } else {
            System.out.println("二叉树为空...");
        }
    }

    /**
     * 非递归方法
     * 前序遍历
     */
    public void preOrder() {
        if (this.root != null) {
            this.root.preOrderTraverse();
        } else {
            System.out.println("二叉树为空");
        }
    }

    /**
     * 递归方法
     * 中序遍历
     */
    public void inorder() {
        if (this.root != null) {
            this.root.inorder();
        } else {
            System.out.println("二叉树为空...");
        }
    }

    /**
     * 非递归方法
     * 中序遍历
     */
    public void inOrder() {
        if (this.root != null) {
            this.root.inOrderTraverse();
        } else {
            System.out.println("二叉树为空");
        }
    }

    /**
     * 递归方法
     * 后序遍历
     */
    public void postorder() {
        if (this.root != null) {
            this.root.postorder();
        } else {
            System.out.println("二叉树为空...");
        }
    }

    /**
     * 非递归方法
     * 后序遍历
     */
    public void postOrder() {
        if (this.root != null) {
            this.root.postOrderTraverse();
        } else {
            System.out.println("二叉树为空");
        }
    }

    public static void main(String[] args) {
        HeroNode root = new HeroNode(1, "宋江");
        HeroNode node2 = new HeroNode(2, "吴用");
        HeroNode node3 = new HeroNode(3, "卢俊义");
        HeroNode node4 = new HeroNode(4, "林冲");
        HeroNode node5 = new HeroNode(5, "关胜");
//        HeroNode node6 = new HeroNode(6, "鲁智深");

        root.setLeftNode(node2);
        root.setRightNode(node3);
//        node2.setRightNode(node6);
        node3.setRightNode(node4);
        node3.setLeftNode(node5);
        BinaryTree binaryTree = new BinaryTree();
        binaryTree.setRoot(root);

        // 递归方法
//        System.out.println("前序遍历");
//        binaryTree.preorder();
//        System.out.println("中序遍历");
//        binaryTree.inorder();
//        System.out.println("后序遍历");
//        binaryTree.postorder();

        // 非递归方法
        System.out.println("前序遍历");
        binaryTree.preOrder();
        System.out.println("中序遍历");
        binaryTree.inOrder();
        System.out.println("中序遍历");
        binaryTree.postOrder();
    }
}

class HeroNode {
    private int id;
    private String name;
    private HeroNode leftNode;
    private HeroNode rightNode;

    public HeroNode(int id, String name) {
        this.id = id;
        this.name = name;
    }

    public int getId() {
        return id;
    }

    public void setId(int id) {
        this.id = id;
    }

    public String getName() {
        return name;
    }

    public void setName(String name) {
        this.name = name;
    }

    public HeroNode getLeftNode() {
        return leftNode;
    }

    public void setLeftNode(HeroNode leftNode) {
        this.leftNode = leftNode;
    }

    public HeroNode getRightNode() {
        return rightNode;
    }

    public void setRightNode(HeroNode rightNode) {
        this.rightNode = rightNode;
    }

    @Override
    public String toString() {
        return "HeroNode{" +
                "id=" + id +
                ", name='" + name + '\'' +
                ", leftNode=" + leftNode +
                ", rightNode=" + rightNode +
                '}';
    }

    /**
     * 递归方法
     * 前序遍历
     */
    public void preorder() {
        // 输出根节点，这里的 this 就是 BinaryTree类 中的成员变量 root，因为 this.root.preorder()
        // this 调用谁，谁就是 this
        System.out.println(this);
        // 向左遍历
        if (this.leftNode != null) {
            this.leftNode.preorder();
        }
        // 向右遍历
        if (this.rightNode != null) {
            this.rightNode.preorder();
        }
    }

    /**
     * 非递归方法
     * 前序遍历
     */
    public void preOrderTraverse() {
        // 定义一个辅助指针指向根节点
        HeroNode temp = this;
        Stack<HeroNode> stack = new Stack<>();
        List<HeroNode> list = new LinkedList<>();
        while (temp != null) {
            // 向左遍历
            while (temp != null) {
                // 将当前节点添加到 list 集合中
                list.add(temp);
                if (temp.getRightNode() != null) {
                    // 如果当前节点的右节点不为空，就先把右节点入栈，存起来，等所有的左节点数据遍历完后，
                    // 再将右节点从栈中取出，继续向左遍历，存储右节点...直到右节点为空
                    stack.push(temp.getRightNode());
                }
                // 将当前节点的指针指向当前节点的左节点
                temp = temp.getLeftNode();
            }

            if (stack.size() > 0) {
                // 将存到栈中右节点取出，即当前节点指针指向右节点，继续上面操作
                temp = stack.pop();
            }
        }
        list.forEach(System.out::println);
    }

    /**
     * 递归方法
     * 中序遍历
     */
    public void inorder() {
        // 向左遍历
        if (this.leftNode != null) {
            this.leftNode.inorder();
        }
        // 输出根节点
        System.out.println(this);
        // 向右遍历
        if (this.rightNode != null) {
            this.rightNode.inorder();
        }
    }

    /**
     * 非递归方法
     * 中序遍历
     */
    public void inOrderTraverse() {
        // 定义一个辅助指针 temp 指向根节点
        HeroNode temp = this;
        List<HeroNode> list = new ArrayList<>();
        Stack<HeroNode> stack = new Stack<>();
        while (temp != null || !stack.isEmpty()) {
            // 一直向左遍历
            while (temp != null) {
                // 将 根节点 入栈
                stack.push(temp);
                temp = temp.getLeftNode();
            }

            if (stack.size() > 0) {
                // 从栈中取出栈顶的 根节点
                temp = stack.pop();
                // 将当前节点添加到 list 集合中
                list.add(temp);
                // 向右遍历
                temp = temp.getRightNode();
            }
        }
        list.forEach(System.out::println);
    }

    /**
     * 递归方法
     * 后序遍历
     */
    public void postorder() {
        // 向左遍历
        if (this.leftNode != null) {
            this.leftNode.postorder();
        }
        // 向右遍历
        if (this.rightNode != null) {
            this.rightNode.postorder();
        }
        // 输出根节点
        System.out.println(this);
    }

    /**
     * 非递归方法
     * 后序遍历
     */
    public void postOrderTraverse() {
        // 定义辅助指针 temp 指向根节点
        HeroNode temp = this;
        List<HeroNode> list = new ArrayList<>();
        Stack<HeroNode> stack = new Stack<>();
        while (temp != null || !stack.isEmpty()) {
            // 一直向左遍历
            while (temp != null) {
                // 将根节点入栈
                stack.push(temp);
                if (temp.getLeftNode() != null) {
                    temp = temp.getLeftNode();
                } else {
                    temp = temp.getRightNode();
                }
            }
            if (stack.size() > 0) {
                // 从栈中取出栈顶元素
                temp = stack.pop();
                // 将当前元素添加到 list 集合中
                list.add(temp);
            }
            // 当栈不为空，且栈顶元素的右节点 = 当前节点，取栈顶元素
            while (stack.size() > 0 && stack.peek().getRightNode() == temp) {
                // 取栈顶元素
                temp = stack.pop();
                // 将当前节点添加到 list 集合中
                list.add(temp);
            }

            // 当栈不为空时，temp 就只指向栈顶元素的右节点
            if (stack.size() > 0) {
                temp = stack.peek().getRightNode();
            } else {
                temp = null;
            }
        }
        list.forEach(System.out::println);
    }
}

运行结果截图

该文章来源于 B站，韩顺平老师的数据结构与算法教程！