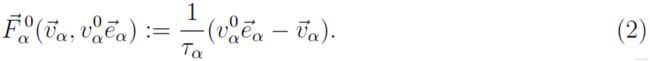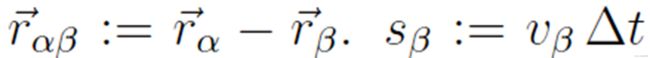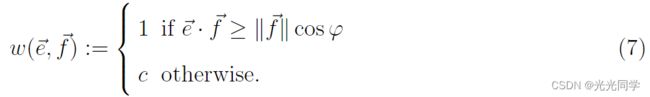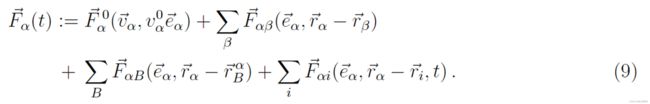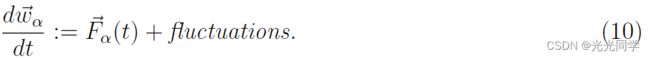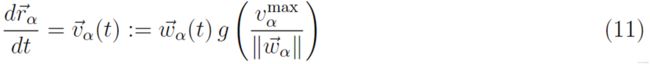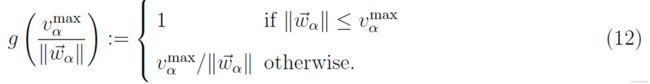【行人轨迹预测经典论文】Social force model for pedestrian dynamics
关键词:行人轨迹预测
阅读总结:
摘要
Social Force 认为行人行为不是由社会环境外力直接作用的,而是行人内在属性驱动的。模型是衡量这种动机的一种度量。模型中有三个核心“力”项:(1)一个描述朝向所需运动速度的加速度的力项;(2)反映行人与其他行人及边界保持一定距离的力项;(3)一个模拟吸引力效果的力项。由此产生的运动方程是非线性耦合的Langevin方程。
1. 简介 (略)
2.模型内容
复杂环境下的人类行为模型是不可预测的,但在相对简单的场景中,随机行为是可以被建模的。
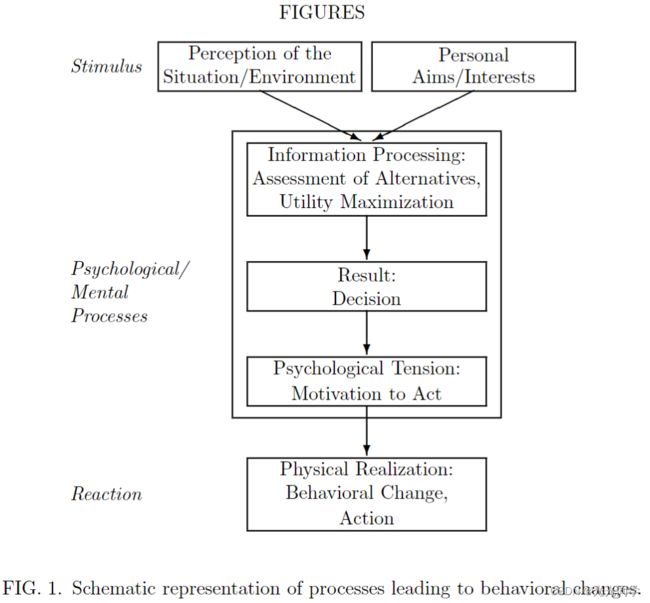
图 1 说明了导致行为变化的过程图。据此,感官刺激会引起行为反应,该反应取决于个人目标,并且是从一组以效用最大化为目标的行为选择中选择的。
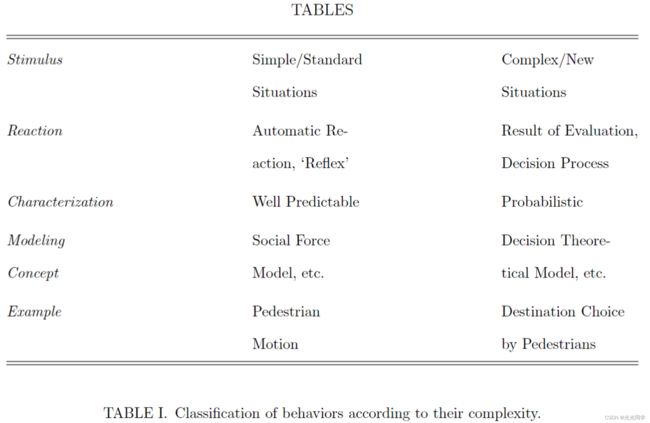
表 1 显示了将刺激分为易于预测的简单或标准情况,以及可以用概率模型建模的复杂或新情况。然而,行人在面临情况时,往往是根据自己的经验来做出自己认为最好且恰当的反应,这种反应是自主的。因此,可以将行人行为的规则放入运动方程中。根据该方程,行人 α 的首选速度 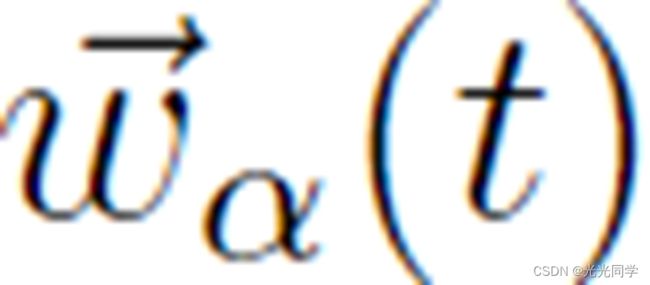 的系统时间变化
的系统时间变化 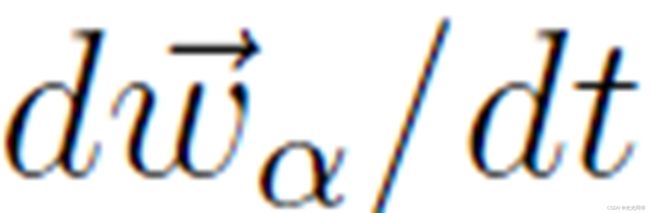 由可解释为社会力量的向量量
由可解释为社会力量的向量量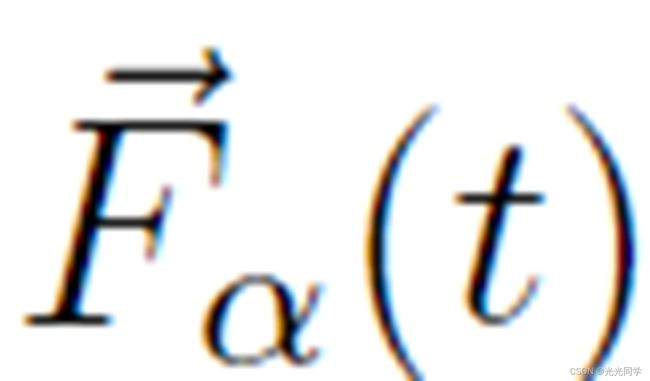 描述。显然,这种力必须代表环境(例如其他行人或边界)对所描述行人行为的影响。然而,社会力量并不是由行人身上的环境所施加的。它是一个描述行动的具体动机的数量。在行人行为的情况下,这种动机会引起加速或减速力的物理产生,作为对他/她获得的关于他/她的环境的感知信息的反应(见图 1)。总之,可以说行人的行为就像他/她会受到外力一样。这个想法已经在数学上建立在参考文献[26]中 。
描述。显然,这种力必须代表环境(例如其他行人或边界)对所描述行人行为的影响。然而,社会力量并不是由行人身上的环境所施加的。它是一个描述行动的具体动机的数量。在行人行为的情况下,这种动机会引起加速或减速力的物理产生,作为对他/她获得的关于他/她的环境的感知信息的反应(见图 1)。总之,可以说行人的行为就像他/她会受到外力一样。这个想法已经在数学上建立在参考文献[26]中 。
3.SFM的公式
模型中三个核心的力:
1.以期望速度到达目标方向的力。(方向力)
人类希望以最短最舒适的速度到达目标点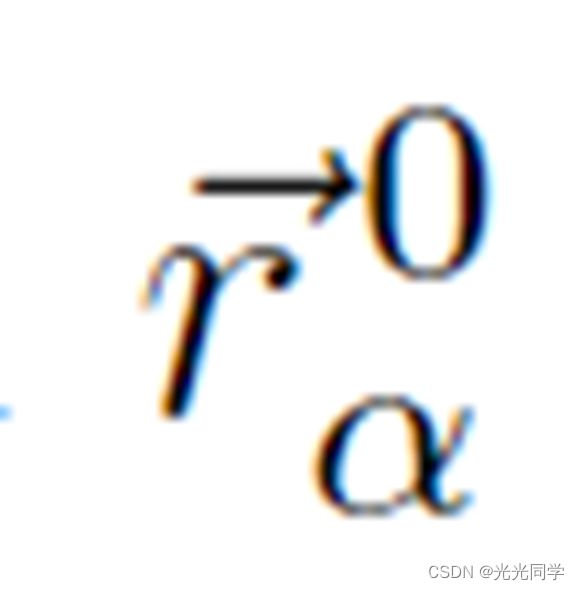 ,目标方向并非一定是直线,也可能连接起始点到目标点的是曲线或者折线,可以用多边形表示
,目标方向并非一定是直线,也可能连接起始点到目标点的是曲线或者折线,可以用多边形表示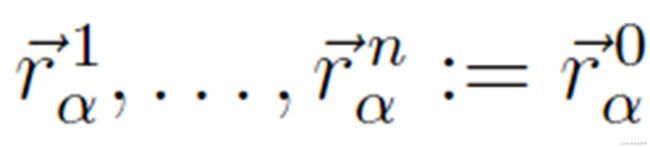 。如果
。如果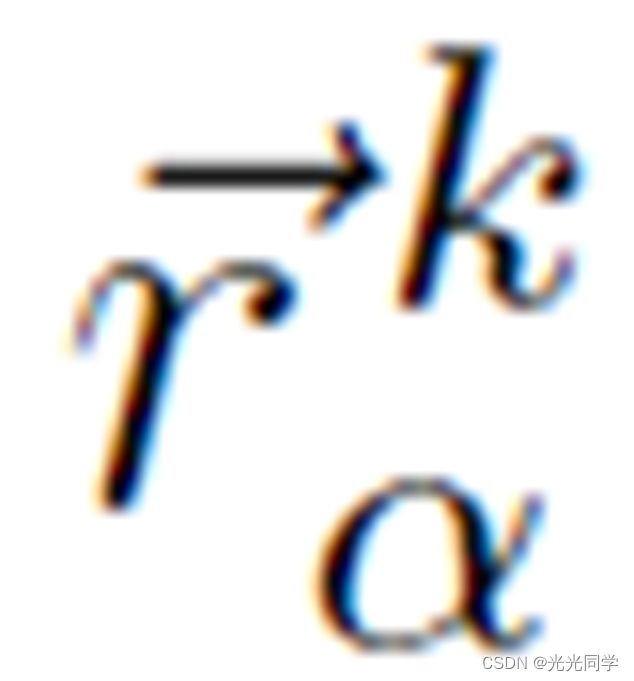 是通向目标点的最后一条边,那么运动方向
是通向目标点的最后一条边,那么运动方向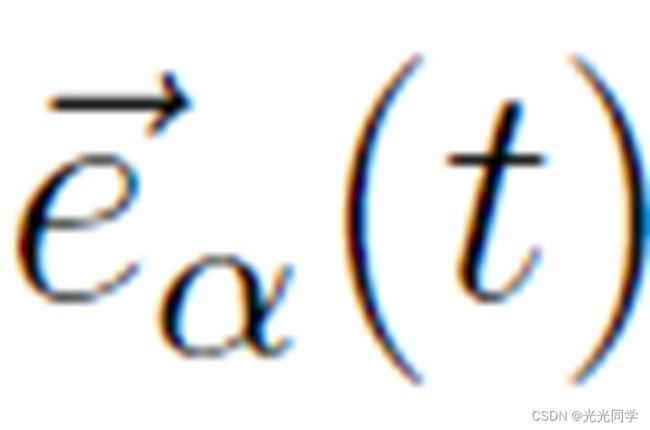 可以表示为:
可以表示为:
其中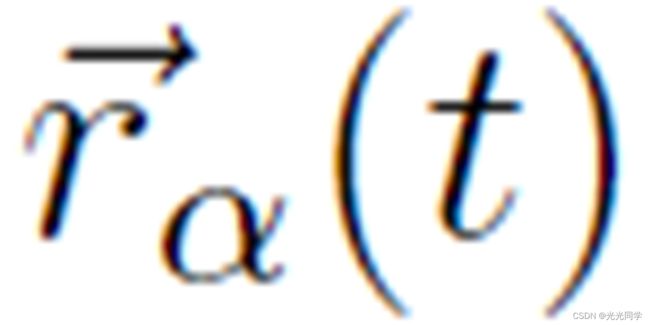 表示行人 α 在时间 t 的实际位置。行人的目标通常是门或区域,而不是点
表示行人 α 在时间 t 的实际位置。行人的目标通常是门或区域,而不是点 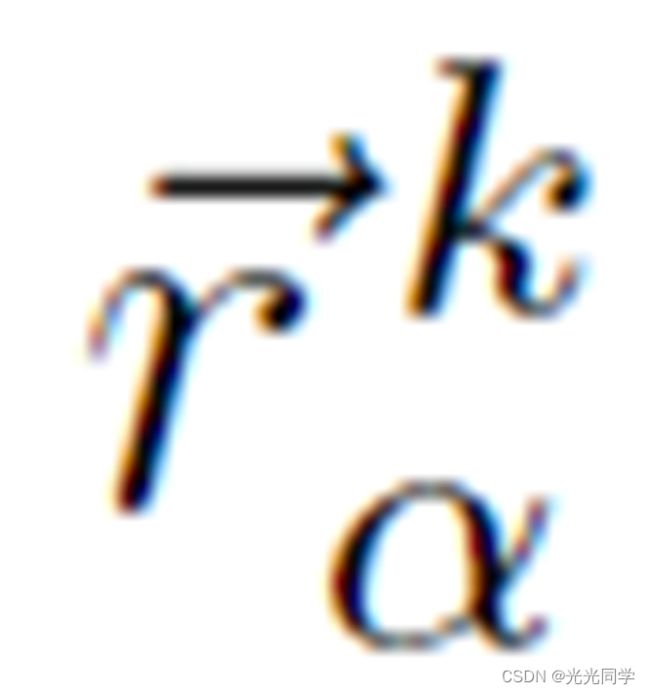 。在这种情况下,他/她将在每次 t 转向相应门/区域的最近点
。在这种情况下,他/她将在每次 t 转向相应门/区域的最近点  。
。
如果行人的运动不受干扰,他/她将以一定的期望速度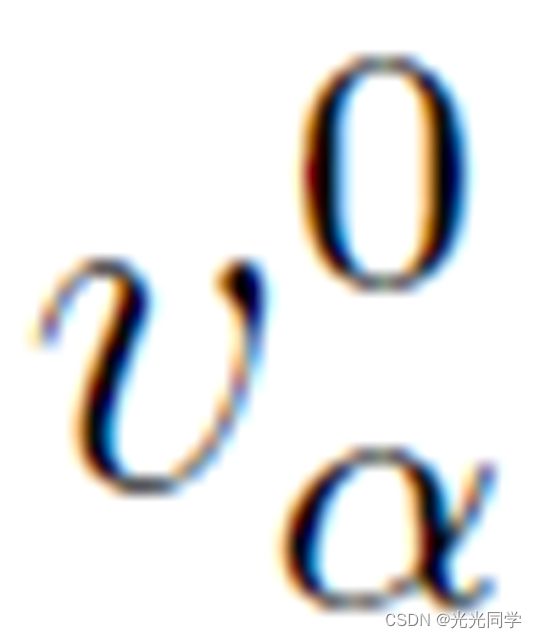 向期望的方向
向期望的方向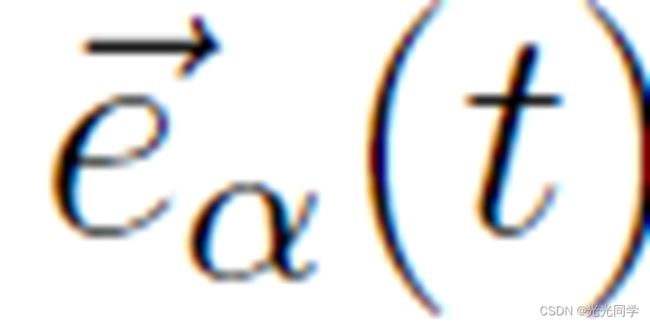 步行。由于必要的减速过程或回避过程,实际速度
步行。由于必要的减速过程或回避过程,实际速度 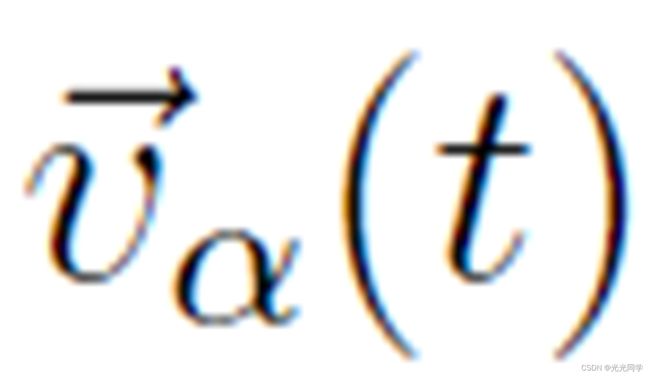 与期望速度
与期望速度 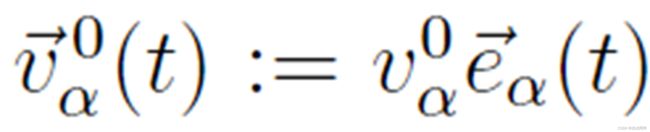 的偏差导致趋向于接近
的偏差导致趋向于接近 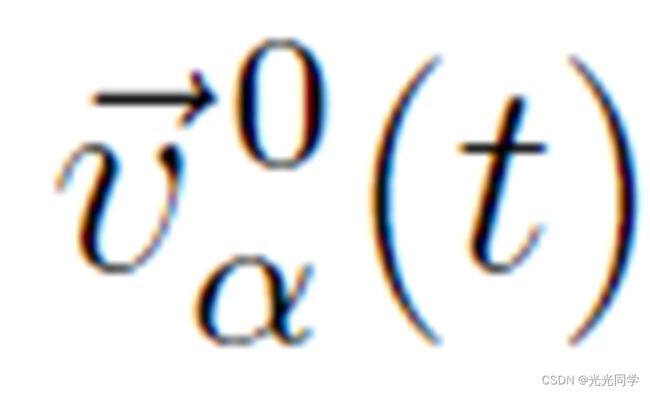 再次在一定的弛豫时间
再次在一定的弛豫时间 内。这可以通过以下形式的加速度项来描述:
内。这可以通过以下形式的加速度项来描述:
2. 潜意识地与其他障碍物保持一定距离的内在力。(排斥力)
行人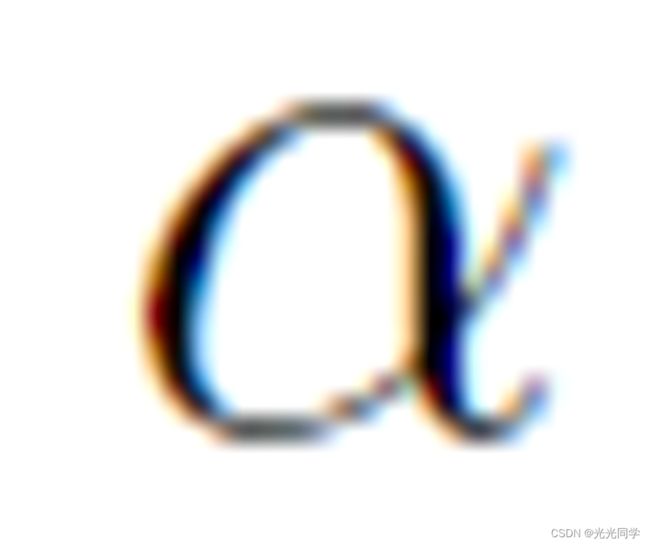 的运动受其他人的影响,根据行人密度和期望速度
的运动受其他人的影响,根据行人密度和期望速度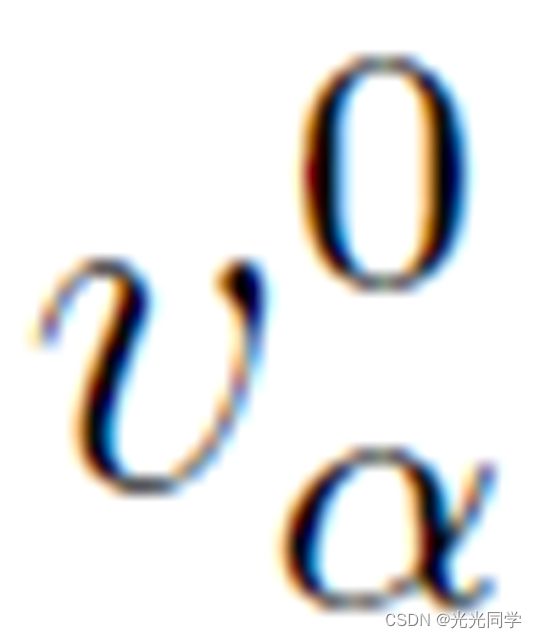 会与其他人会保持一定的距离。根据领土效应以及来自行人
会与其他人会保持一定的距离。根据领土效应以及来自行人 排斥反应的结果可以用矢量来表示:
排斥反应的结果可以用矢量来表示:
假设排斥势 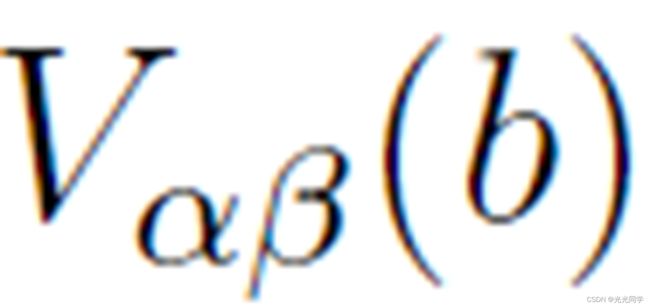 是 b 的单调递减函数,其等势线具有指向运动方向的椭圆形式。这样做的原因是行人需要空间来进行下一步,其他行人会考虑到这一点。 b 表示椭圆的短半轴,由下式给出:
是 b 的单调递减函数,其等势线具有指向运动方向的椭圆形式。这样做的原因是行人需要空间来进行下一步,其他行人会考虑到这一点。 b 表示椭圆的短半轴,由下式给出:
除此之外,行人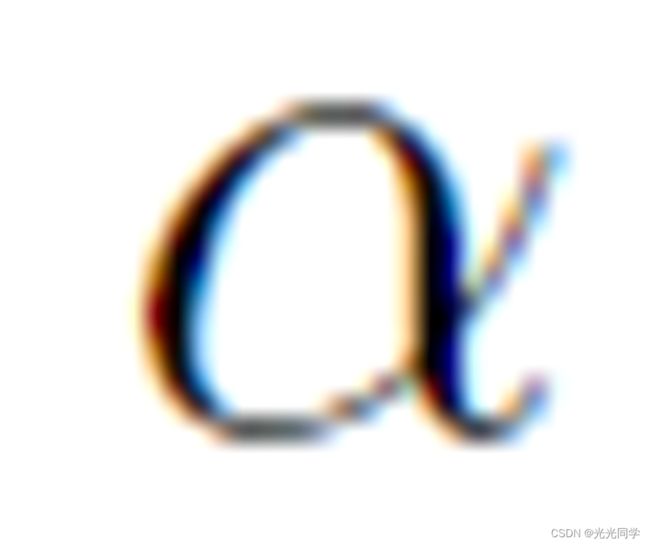 与环境中的道路边界B等也会有一定的排斥作用,表示为:
与环境中的道路边界B等也会有一定的排斥作用,表示为:
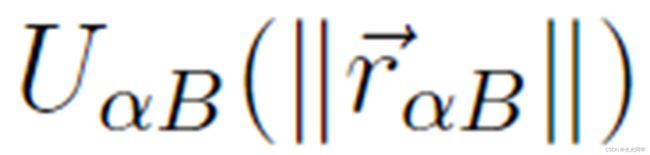 表示排斥和单点递减的势力,这里,向量
表示排斥和单点递减的势力,这里,向量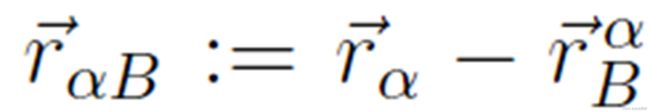 已经被引入,其中
已经被引入,其中 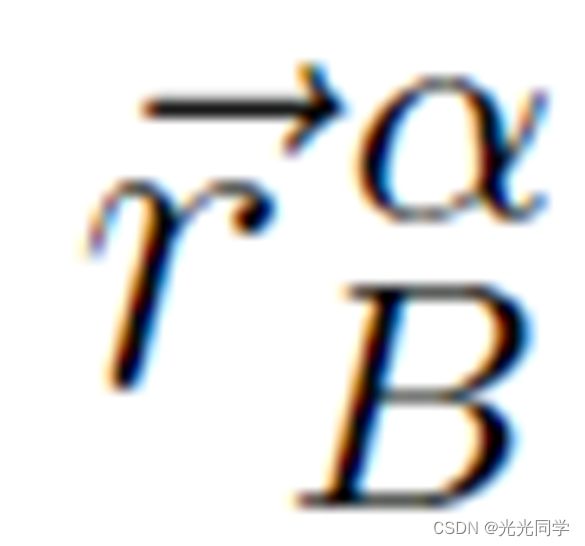 表示最接近行人 α 的那条边界 B 的位置。
表示最接近行人 α 的那条边界 B 的位置。
3. 其他事物对行人的吸引力。(吸引力)
这些在位置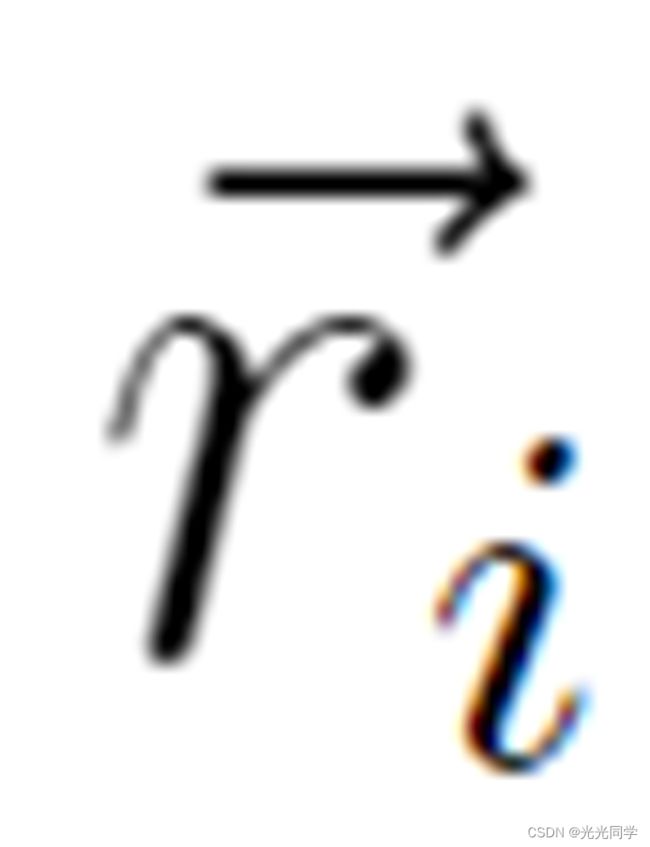 的吸引效应
的吸引效应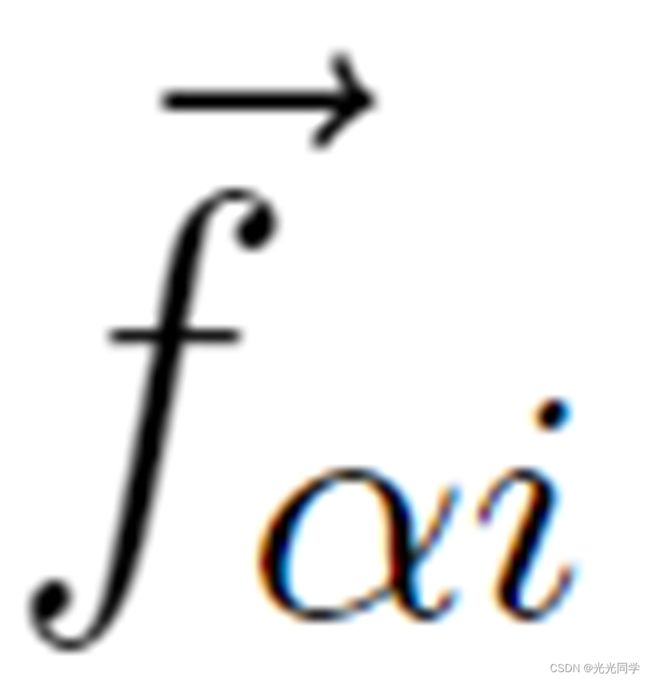 可以通过吸引的、单调递增的势
可以通过吸引的、单调递增的势 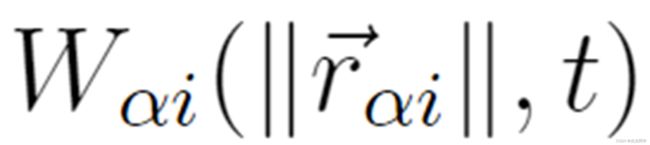 以类似于排斥效应的方式建模:
以类似于排斥效应的方式建模:
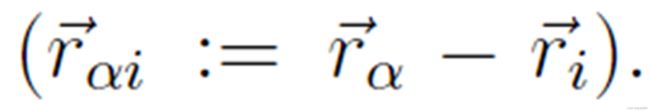 主要区别在于吸引力
主要区别在于吸引力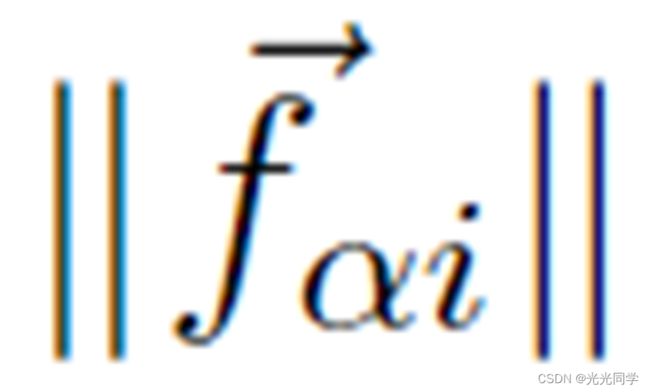 通常随着时间 t 下降,因为兴趣正在下降。吸引人的影响是,例如,负责形成行人群体(可与分子相媲美)。
通常随着时间 t 下降,因为兴趣正在下降。吸引人的影响是,例如,负责形成行人群体(可与分子相媲美)。
然而,上述关于吸引和排斥效应的公式仅适用于在所需运动方向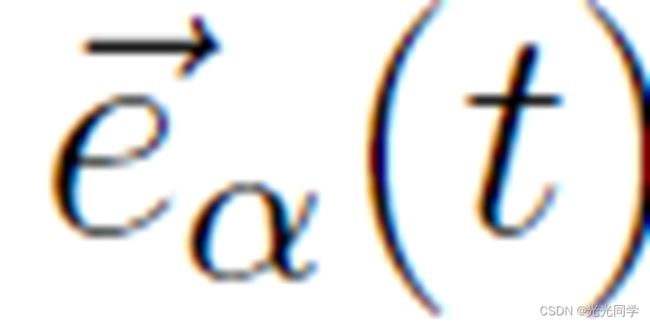 上感知的情况。位于行人后面的情况对 c 的影响较小,其中0 < c < 1。为了考虑这种感知效果(即有效视角 2φ),我们必须引入与方向相关的权重。
上感知的情况。位于行人后面的情况对 c 的影响较小,其中0 < c < 1。为了考虑这种感知效果(即有效视角 2φ),我们必须引入与方向相关的权重。
总之,对行人行为的排斥和吸引效应由下式给出
总动力方程:
SFM定义为:
方程中添加了一个波动项fluctuation term,它考虑了行为的随机变化。一方面,这些波动源于两个或多个行为选择是等价的模棱两可的情况(例如,如果通过右侧或左侧的障碍物的效用相同)。另一方面,波动是由于意外或故意偏离通常的运动规则而产生的。
为了完成行人动力学模型,必须引入实际速度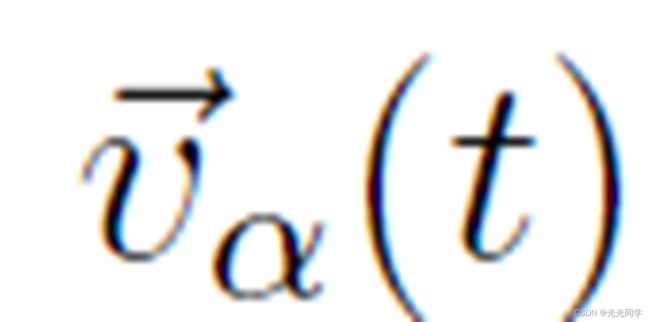 和首选速度
和首选速度 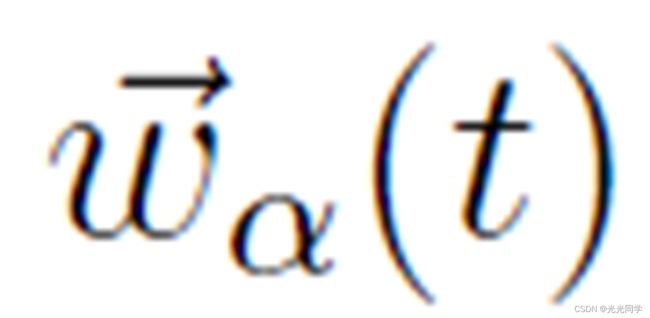 之间的关系。由于实际速度受行人最大可接受速度
之间的关系。由于实际速度受行人最大可接受速度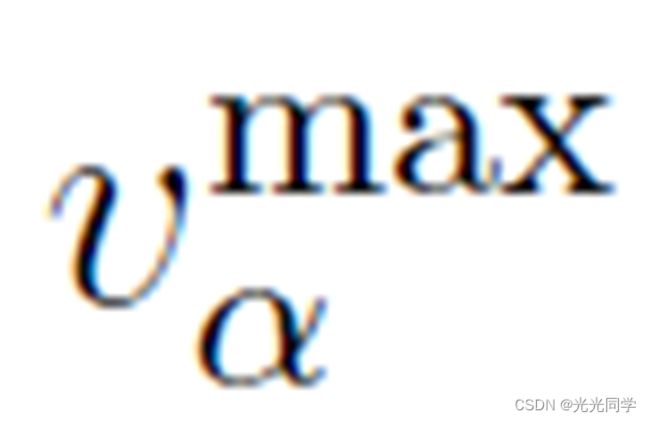 的限制,我们将假设实现的运动由下式给出:
的限制,我们将假设实现的运动由下式给出:
其中:
注意,行人模型(10)、(11)具有非线性耦合朗之万方程的形式。它的简化版本可以扩展到主动步行模型[28-30],用于路系统的自组织[31]。这与蚂蚁对树干轨迹形成的数学描述有关 [32] 。
4. 计算模拟
第三节中开发的行人动力学模型已经在计算机上模拟了大量面临不同情况的交互行人。尽管提出的模型非常简单,但它非常真实地描述了许多观察到的现象。下面,将展示两个例子来展示行人行为的集体现象的自组织。
模拟假设所需的速度  是高斯分布的 [4,7],均值
是高斯分布的 [4,7],均值 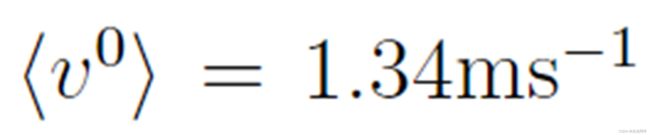 ,标准偏差
,标准偏差 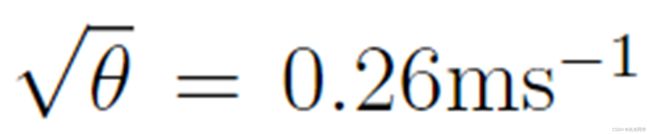 [33]。速度限制在
[33]。速度限制在 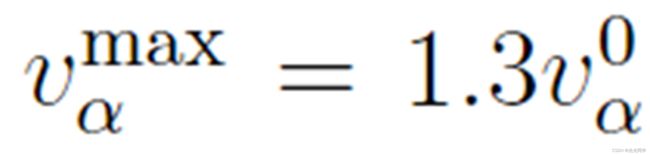 。行人从随机位置进入人行道的尽头。那些打算从左边走到右边的人用实心圆圈表示,而打算向相反方向移动的行人用空心圆圈表示。圆的直径是衡量行人 α 的实际速度
。行人从随机位置进入人行道的尽头。那些打算从左边走到右边的人用实心圆圈表示,而打算向相反方向移动的行人用空心圆圈表示。圆的直径是衡量行人 α 的实际速度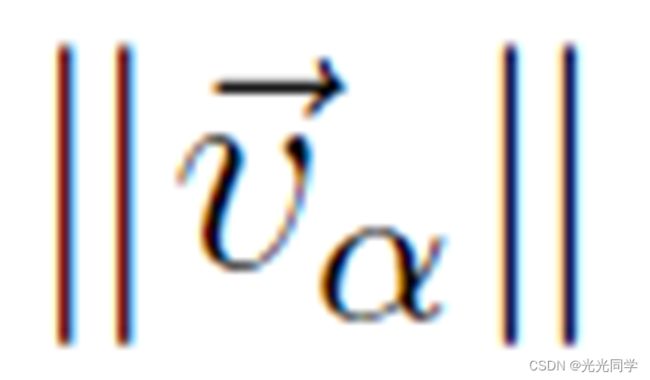 的量度。为简单起见,没有考虑吸引效应
的量度。为简单起见,没有考虑吸引效应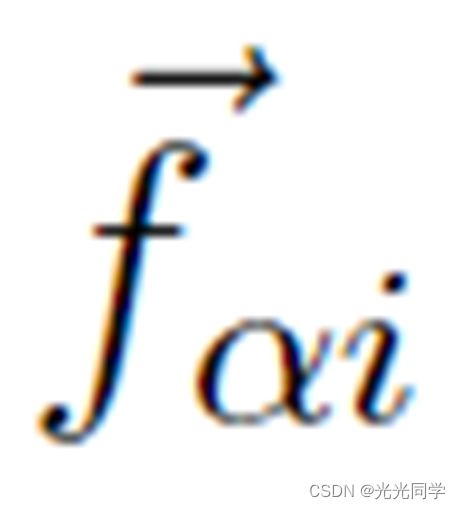 或波动。假定排斥势呈指数下降,即
或波动。假定排斥势呈指数下降,即
![]()
其中,。当然,具有硬核的可能性会更真实,但它们不会产生其他结果,因为模拟的行人总是保持足够的距离。
人行道选择 10m 宽。对于公式 (4) 中的 Δt,我们采用 Δt = 2s,对于弛豫时间,我们采用 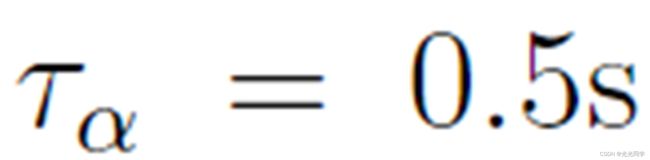 。较小的
。较小的  值让行人走得更有侵略性。最后,有效视角(也考虑了头部运动)设置为 2φ = 200°。假定视角以外的情况具有 c = 0.5 的影响。上面介绍的模型参数是以与经验数据兼容的方式选择的。
值让行人走得更有侵略性。最后,有效视角(也考虑了头部运动)设置为 2φ = 200°。假定视角以外的情况具有 c = 0.5 的影响。上面介绍的模型参数是以与经验数据兼容的方式选择的。
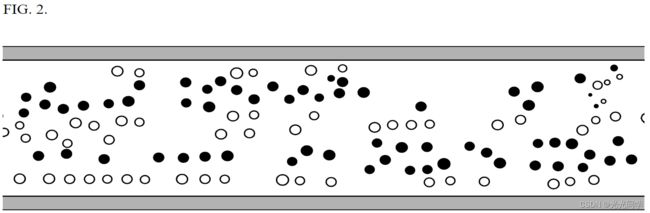
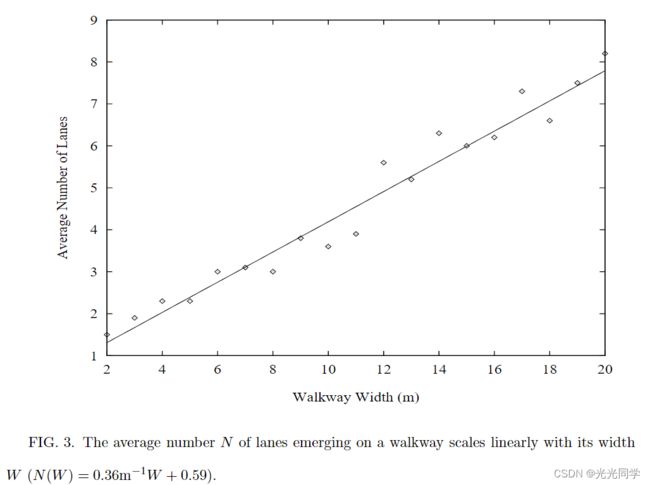
图 2 显示了经经验证实的 [6] 动态变化车道的发展,这些车道由打算走向同一方向的行人组成。横向上的周期性边界条件将稳定这些车道,因为它们在人行道的末端不再被随机进入的行人破坏[2,21]。图 3 显示了行人密度为 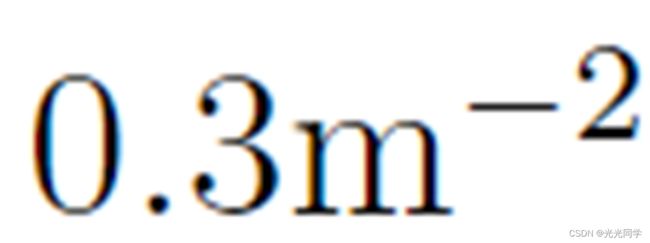 时形成车道的数量与人行道宽度的关系。
时形成车道的数量与人行道宽度的关系。
如图 2. 在临界行人密度之上,可以观察到由具有统一步行方向的行人组成的车道的形成。在这里,计算结果显示在一条宽 10m 长 50m 的人行道上有 N = 4 条车道。空心圆代表具有与实心圆所表示的行人相反的期望运动方向的行人。
车道形成的隔离效应不是初始行人配置的结果,而是行人相互作用的结果。尽管如此,它通常会导致更有效的行人流,因为耗时的回避操作发生的频率较低。
图 4 和图 5 描绘了两个行人组试图通过窄门进入相反方向的不同时刻。相应的模拟显示如下:一旦行人通过门,其他打算向同一方向移动的行人能够轻松地跟随他/她(见图4)。然而,经过一段时间后,过往的行人被对方的压力拦住了。随后,门被从相反方向通过的行人捕获(见图 5)。这种通过方向的变化可能会发生多次,并且从观察中是众所周知的。
5. 总结与展望
已经表明,行人运动可以通过一个简单的个人行人行为的社会力模型来描述。行人群体的计算机模拟表明 1. 由向同一方向行走的行人组成的车道的发展, 2. 在狭窄通道中行走方向的振荡变化。这些时空模式是由于行人的非线性相互作用而产生的。它们不是个别行人的战略考虑的结果,因为他们被假定以一种相当“自动”的方式行事。
目前,社会力模型被扩展为行人路径选择行为模型。一旦计算机程序完成,它将为城镇和交通规划提供一个舒适的工具。行人行为的调查是开发其他或更一般的定量行为模型的理想起点,因为行人运动的变量很容易测量,因此相应的模型与经验数据具有可比性。进一步的步骤可能是将社会力量概念应用于描述意见形成、群体动态或其他社会现象 [26]。为此,必须引入抽象的行为空间。