Python数据特征分析1-分布分析(极差,频率直方图等)
数据特征分析分为以下部分:
1.分布分析
2.对比分析
3.统计分析
4.帕累托分析
5.正态性检验
6.相关性分析
数据:
分布分析
分布分析 --> 研究数据的分布特征和分布类型,分定量数据、定性数据
主要是:极差、频率分布情况、分组组距及组数
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings('ignore')
数据预览
数据集-验证码wiaz
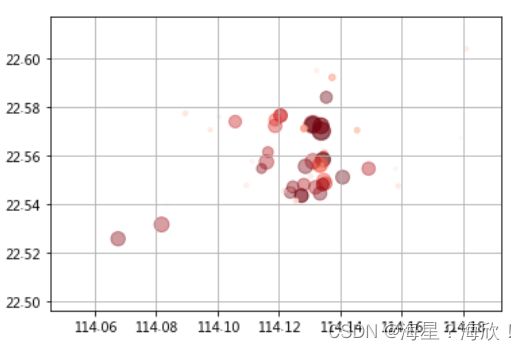
#作散点图:横纵轴放经纬度,单价显示大小,总价显示颜色
data = pd.read_csv('E:/shuju/数据特征分析/second_hand_ house.csv')
data.head()
plt.scatter(data['经度'],data['纬度'],s = data['房屋单价']/500,c=data['参考总价'],alpha=0.4,cmap = 'Reds')
plt.grid()
print(data.dtypes) #显示各列类型
print('------\n数据长度%i条'%len(data)) #输出数据长度
极差–对定量字段
#定义(可以求多列的极差)的函数
def d_range(df,*cols):
krange = []
for col in cols:
crange = df[col].max()- df[col].min()
krange.append(crange)
return krange
key1 = '参考首付'
key2 = '参考总价'
dr = d_range(data,key1,key2)
print('%s的极差为%f \n%s的极差为%f'%(key1,dr[0],key2,dr[1]))
频率分布情况 - 对定量字段
1.通过直方图直接判断分组组数
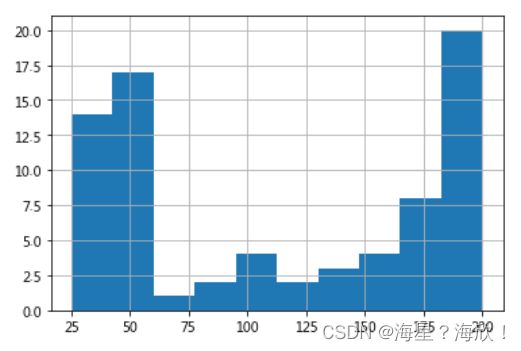
#分组做柱状图
data[key2].hist(bins=10)
#简单查看数据分布,确定分布组数 → 一般8-16即可.这里分10组
pd.cut() 分箱
pd.cut(x,bins,right=True,labels=None,retbins=False,precision=3,include_lowest=False,duplicates=‘raise’)
x : 一维数组
bins :整数,标量序列或者间隔索引,是进行分组的依据,
如果填入整数n,则表示将x中的数值分成等宽的n份(即每一组内的最大值与最小值之差约相等);
如果是标量序列,序列中的数值表示用来分档的分界值
right :布尔值,默认为True表示包含最右侧的数值,即区间是左开右闭的
value_counts常用于数据表的计数及排序,计算每个不同值有在该列中的个数,同时还能根据需要进行排序。
gcut = pd.cut(data[key2],10,right=False)
gcut_count = gcut.value_counts(sort=False)
#在这里不排序
data['%s分组区间' % key2] = gcut.values
#给原表多加一列,写每列数据在的区间
print(gcut.head(),'\n------')
print(gcut_count)
data.head()
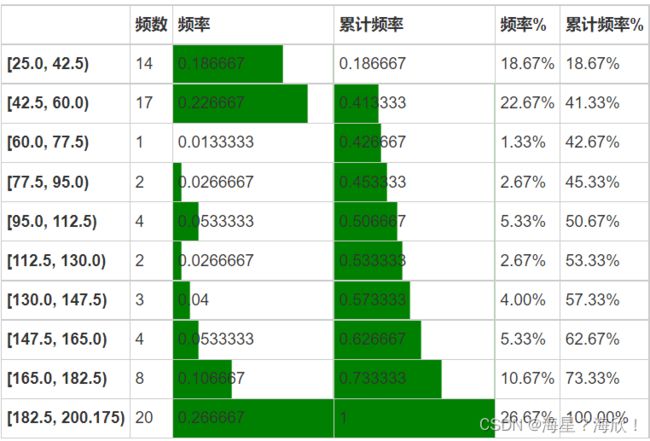
3,求出目标字段下频率分布的其他统计量 → 频数,频率,累计频率
**pd.DataFrame()**创建DataFrame格式
DataFrame是Python中Pandas库中的一种数据结构,它类似excel,是一种二维表。
r_zj = pd.DataFrame(gcut_count)
r_zj.rename(columns ={gcut_count.name:'频数'}, inplace = True) # 修改频数字段名
r_zj['频率'] = r_zj / r_zj['频数'].sum() # 计算频率
r_zj['累计频率'] = r_zj['频率'].cumsum() # 计算累计频率
r_zj['频率%'] = r_zj['频率'].apply(lambda x: "%.2f%%" % (x*100)) # 以百分比显示频率
r_zj['累计频率%'] = r_zj['累计频率'].apply(lambda x: "%.2f%%" % (x*100)) # 以百分比显示累计频率
r_zj.style.bar(subset=['频率','累计频率'], color='green',width=100)
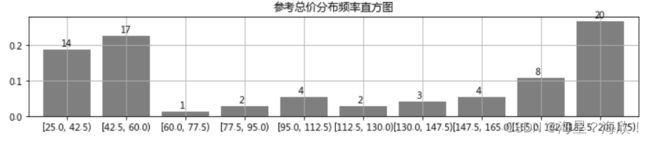
r_zj['频率'].plot(kind = 'bar',width = 0.8,figsize = (12,2),rot=0,color = 'k',grid=True,alpha = 0.5)
plt.title('参考总价分布频率直方图')
x = len(r_zj)
y = r_zj['频率']
m = r_zj['频数']
for i,j,k in zip(range(x),y,m):
plt.text(i-0.1,j+0.01,'%i'%k,color = 'k')
#添加频数标签
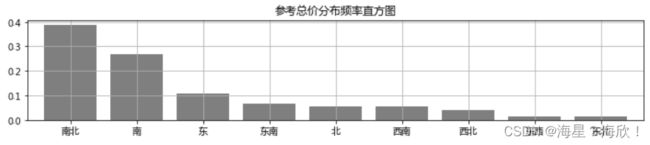
频率分布情况 - 对定性字段
1,通过计数统计判断不同类别的频率
cx_g = data['朝向'].value_counts(sort=True)
print(cx_g) # 统计频率,且排了序
r_cx = pd.DataFrame(cx_g)
r_cx.rename(columns ={cx_g.name:'频数'}, inplace = True) # 修改频数字段名
r_cx['频率'] = r_cx / r_cx['频数'].sum() # 计算频率
r_cx['累计频率'] = r_cx['频率'].cumsum() # 计算累计频率
r_cx['频率%'] = r_cx['频率'].apply(lambda x: "%.2f%%" % (x*100)) # 以百分比显示频率
r_cx['累计频率%'] = r_cx['累计频率'].apply(lambda x: "%.2f%%" % (x*100)) # 以百分比显示累计频率
r_cx.style.bar(subset=['频率','累计频率'], color='#d65f5f',width=100)
plt.figure(num = 1,figsize = (12,2))
r_cx['频率'].plot(kind = 'bar',
width = 0.8,
rot = 0,
color = 'k',
grid = True,
alpha = 0.5)
plt.title('参考总价分布频率直方图')
# 绘制直方图
plt.figure(num = 2)
plt.pie(r_cx['频数'],
labels = r_cx.index,
autopct='%.2f%%',
shadow = True)
plt.axis('equal')
# 绘制饼图