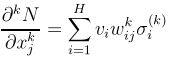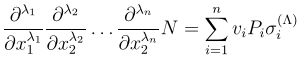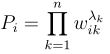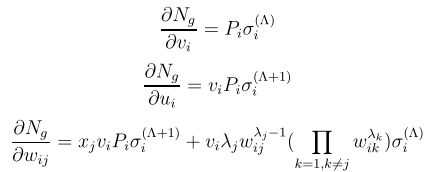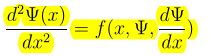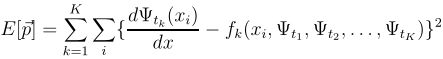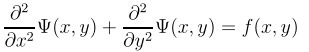求解常和偏微分方程的人工神经网络
Artificial Neural networks for Solving Ordinary and Partial Differential Equations
文章目录
- 系列文章目录
- 前言
- 一、背景介绍
- 二、方法描述
- 1.梯度计算
- 三、方法说明
1单元常微分方程与多元常微分方程 - 2 Solution of single PDEs
- 四、例子
- 4.1 ODEs and systems of ODEs
- 4.2 PDEs
- 4.3 Comparison with Finite Elements
- 五、总结
前言
本文提出了一种运用神经网络解决最初值和边界初始值问题；微分方程的解决方法写成了两部分。
第一部分满足满足最初值和约束值条件，并且包含不能改变的参数；
第二部分的创建是为了不影响第一部分；这一部分设计神经网络，包含了可调整的参数；神经网络部分被训练来满足微分方程。这个方法适用于单一常微分方程，和多元常微分方程；
在本篇文章中，方法能解决各种各样的问题并与有限元方法在偏微分方程的几个例子中做出了比较。
一、背景
目前为止，已经发展了许多方法来解微分方程。其中一些以数组的形式产生解决方案，其中包含一组选定点上的解决方案的值。另一些则用基函数来表示解析形式的解，并将原问题转换成线性方程组。以往利用神经网络求解微分方程的工作大多局限于求解由区域离散化而产生的线性代数方程组。线性方程组的解映射到Hopfield神经网络的体系结构上。网络能量函数的最小化提供了方程组的解。
另一种方法对于常微分方程的解是基于某些类型的样条，例如线性b样条，可以通过分段线性激活函数的叠加得到。用线性b样条作为基函数的微分方程的解，可以通过求解线性或非线性方程组来确定样条的参数。这种解的形式直接映射到前馈神经网络的体系结构上，将每条样条替换为与隐藏单元对应的分段线性激活函数的和。该方法考虑局部基函数，一般需要许多样条(因此需要网络参数)，以产生精确的解。此外，将这些技术扩展到多维领域并不容易。
在这篇文章中，我们从不同的角度来看待这个问题。我们提出了一种求解常微分方程(ode)和偏微分方程(PDEs)的一般方法，它依赖于前馈神经网络的函数逼近能力，并得到了一个可微分的封闭解析形式的解的构造。这种形式采用前馈神经网络作为基本的近似元素，其参数(权值和偏差)被调整以使适当的误差函数最小化。为了训练网络，我们采用了优化技术，这反过来要求计算关于网络参数的误差梯度。在该方法中，模型函数表示为两项的和:第一项满足初始/边界条件，不包含可调参数。第二项是要训练一个前馈神经网络以满足微分方程。由于已知带有一个隐含层的多层感知器可以以任意精度逼近任何函数，因此可以将这种类型的网络体系结构作为处理微分方程的候选模型
神经结构的使用为该方法增加了许多吸引人的特点:
（1）通过ANN的解是一个可微的，封闭的解析形式，很容易用于任何后续的计算。大多数其他技术提供了一种离散的解决方案
（2）这种解决方案的特点是神经网络的泛化性质
（3）所需的模型参数数量远少于任何其他解决方案技术，因此，紧凑的解决方案模型，对内存空间的需求非常低。
（4）该方法具有通用性，适用于偏微分方程、偏微分方程系统和偏微分方程。
（5）该方法可以在硬件上实现，使用神经处理器，因此提供了解决实时困难的微分方程问题的机会，在许多工程应用
（6）该方法也可以有效地在并行体系结构上实现。
在下一节中，我们描述了提出的方法的一般公式，并推导了计算误差函数梯度的公式。第3节说明了可以应用所提出方法的一些类别的问题，并描述了试解的适当形式。第四节给出了将该技术应用于几个测试问题的数值例子，并提供了有关该方法的实施和所得到解的精度的细节。我们还将所得结果与所研究的偏微分方程问题的有限元方法所得结果进行了比较。最后，第六部分是结论和未来的研究方向。
二、方法描述
1.一般微分方程描述如下
离散化X区域和边界条件D,得到如下方程：
加入可调参数p:方程转变为
其中：
这里
是一个前馈神经网络的输出，参数p,n个节点的x向量；
即为第一部分，含不可调参数，满足边界；F不需要满足BC,它使用一个神经网络，它的权值和偏差是要调整的，以处理最小化问题。注意，在这一点上，问题已经从原始的有约束优化问题减少到一个无约束问题。
2.梯度计算
在计算误差关于网络权值的梯度时，我们不仅需要计算网络的梯度，还需要计算网络导数关于其输入的梯度。
考虑一个有n个输入单位的多层感知器，一个有H个sigmod隐藏层和一个线性输出单位。其他的网络以此类推；
输入：
结果输出：
其中：
表示从输入单位j到隐藏单位i的权值，
表示从隐藏层到输出的权重，
隐含单元i的偏差.
是sigmod函数。
，这里
，
表示sigmod的k阶导数。
推导过程：
，这里满足
，
。
推出：（这里不太了解原文）
三、方法说明
3.1单常微分方程和耦合常微分方程组的解
求一阶常微分方程：
，
。
解的形式设置如下：
，损失函数为：
类似求二阶常微分方程：
，
满足初值条件：
，解的形式设置如下：
或者两点值条件：
，解的形式设置如下：
这两个二阶常微分方程损失函数：。
对于K个一阶微分方程：
，满足
，解的形式设置：
损失函数最小化：
3.2单个偏微分方程的解
这里我们仅仅考虑二维问题：以此类推到更多维的情况。
(点值边界)
，满足：
，BC:
。解的形式设置如下：
, 这里的A函数是用来满足满足BC。
即：
满足混合边界条件
,
解的形式设置如下：
。同样
满足(BCS):
以上偏微分方程问题损失函数：
，
。
4 举例
这部分，我们将报告许多模型问题的解决方案。在所有情况下，我们都使用多层感知器，它有一个隐含层，包含10个隐含单元和一个线性输出单元，隐藏层是sigmod。在每个问题中精确解
是已知的。从而我们可以衡量获得解的精确性：
。
为了优化最小化损失函数，我们使用了一些Merlin优化包。最终，比较几个算法下来，选择了BFGS算法。
为了说明我们神经网络提供的解决方法，我们提供了在训练集和测试集上相应的差分：
。对于常微分方程ODES,我们还考虑了训练间隔之外的点，以获得解的外推能力的估计。
4.1单常微分方程和耦合常微分方程组的解
4.1.1问题1
，条件：
，精确解：
根据第三部分：可设解为
总结
提示：这里对文章进行总结：
例如：以上就是今天要讲的内容，本文仅仅简单介绍了pandas的使用，而pandas提供了大量能使我们快速便捷地处理数据的函数和方法。