NLP:语言模型与n元语法
语言模型
前言
DCP用到了Transformer,其很多实现的Motivation都来自于Sq2Sq的启发。所以重新回顾学习语言模型。
Reference: 《Dive into Deep Learning》
语言模型
语言模型是自然语言处理的重要技术。自然语言处理中最常见的数据是文本数据。 我们可以把一段自然语言文本看做一段离散的时间序列。假设一段长度为T的文本中的词依次为 w 1 , w 2 , . . . , w T w_1,w_2,...,w_T w1,w2,...,wT, 那么在离散的时间序列中, w t ( 1 ≤ t ≤ T ) w_t(1 \le t \le T ) wt(1≤t≤T)可以看做在时间步t的输出。给定一个长度为T的词的序列 w 1 , w 2 , . . . , w T w_1,w_2,...,w_T w1,w2,...,wT。语言模型将计算该序列的概率:
P ( w 1 , w 2 , . . . , w T ) P(w_1,w_2,...,w_T) P(w1,w2,...,wT)
语言模型的计算
假设序列 w 1 , w 2 , . . . , w T w_1,w_2,...,w_T w1,w2,...,wT中的各个词是依次生成的,我们有:
P ( w 1 , w 2 , . . . w T ) = ∏ t = 1 T P ( w t ∣ w 1 , . . . , w t − 1 ) P(w_1,w_2,...w_T) = \prod\nolimits_{t = 1}^{\rm{T}} {P(w_t|w_1,...,w_{t-1})} P(w1,w2,...wT)=∏t=1TP(wt∣w1,...,wt−1)
例如,一段含有四个词的文本序列的概率:
P ( w 1 , w 2 , w 3 , w 4 ) = P ( w 1 ) P ( w 2 ∣ w 1 ) P ( w 3 ∣ w 1 , w 2 ) P ( w 4 ∣ w 1 , w 2 , w 3 ) P(w_1,w_2,w_3,w_4) = P(w_1)P(w2|w_1)P(w_3|w_1,w_2)P(w_4|w_1,w_2,w_3) P(w1,w2,w3,w4)=P(w1)P(w2∣w1)P(w3∣w1,w2)P(w4∣w1,w2,w3)
为了计算语言模型,我们需要计算词的概率,以及一个词在给定的前几个词的情况下的条件概率,即语言模型参数。设训练数据集为一个大型文本语料库,词的概率可以通过该词在训练数据集中的相对词频来计算。例如, P ( w 1 ) P(w_1) P(w1)可以计算为 w 1 w_1 w1在训练数据集中的词频与训练数据集的总词数之比。因此,根据条件概率定义,一个词在给定前几个词的情况下的条件概率也可以通过训练数据集中的相对词频计算。例如 P ( w 2 ∣ w 1 ) P(w_2|w_1) P(w2∣w1)可以计算为 w 1 , w 2 w_1,w_2 w1,w2两词相邻的频率与 w 1 w_1 w1词频的比值,即 P ( w 1 , w 2 ) P(w_1,w_2) P(w1,w2)与 P ( w 1 ) P(w_1) P(w1)之比。以此类推。
n元语法
当序列长度增加时,计算和存储多个词共同出现的概率的复杂度会呈指数级增加。n元语法通过马尔可夫假设(并不一定成立)简化了语言模型的计算。这里的马尔科夫假设是指一个词的出现如果只与前面n个词相关,即n阶马尔科夫链。如果 n = 1 n=1 n=1,那么有: P ( w 3 ∣ w 1 , w 2 ) = P ( w 3 ∣ w 2 ) P(w_3|w_1,w_2) = P(w_3|w_2) P(w3∣w1,w2)=P(w3∣w2)。如果基于 n − 1 n-1 n−1阶马尔科夫链,我们可以将语言模型改写为:
P ( w 1 , w 2 , . . . , w T ) ≈ ∏ t = 1 T P ( w t ∣ w t − ( n − 1 ) , . . . , w t − 1 ) P(w_1,w_2,...,w_T) \approx \prod\nolimits_{t=1}^{\rm{T}} {P(w_t|w_{t-(n-1)},...,w_{t-1})} P(w1,w2,...,wT)≈∏t=1TP(wt∣wt−(n−1),...,wt−1)
以上称为n元语法(n-grams)。它是基于n-1阶马尔科夫链的概率语言模型。当n分别为1,2和3时,我们将其分别称作一元语法(unlgram)、二元语法(blgram)和三元语法(trlgram)。例如,长度为4的序列 w 1 , w 2 , w 3 , w 4 w_1,w_2,w_3,w_4 w1,w2,w3,w4在一元语法,二元语法和三元语法中的概率分别为:
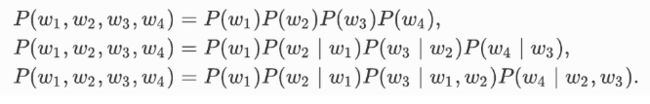
当n较小时,n元语法往往并不准确。