图或网络中的中心性:点度中心性、中介中心性、接近中心性、特征向量中心性、PageRank
文章目录
-
-
- 点度中心性(degree centrality)
- 中介中心性(betweenness centrality)
- 接近中心性(closeness centrality)
- 特征向量中心性(eigenvector centrality)
- 有向图与PageRank
- 小结
-
网络由节点(node)和连接它们的边(edge)构成。例如,微信好友的关系是相互的,如果我是你的好友,你也是我的好友。这样的网络称为无向网络(undirected graph/network)。但超链接并非如此,如果我的网站可以链接到维基百科,并不表示维基百科会链接到我的网站。这样的网络称为有向网络(directed graph/network)。
在图论和网络分析中,中心性(Centrality)是判断网络中节点重要性/影响力的指标。在社会网络分析中,一项基本的任务就是鉴定一群人中哪些人比其他人更有影响力,从而帮助我们理解他们在网络中扮演的角色。
那么,什么样的节点是重要的呢?
对节点重要性的解释有很多,不同的解释下判定中心性的指标也有所不同。
点度中心性(degree centrality)
在无向网络中,我们可以用一个节点的度数(相当于你的微信好友数)来衡量中心性。在微博中,谢娜的粉丝数9千多万,她的点度中心性就很高。
这一指标背后的假设是:重要的节点就是拥有许多连接的节点。你的社会关系越多,你的影响力就越强。
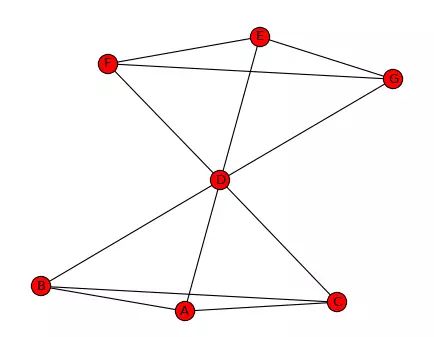
图1:使用networkx绘制的蝴蝶结网络
在上面的蝴蝶结网络中,节点D的连接数是6,和网络中的所有人都建立了直接联系,其他节点的连接数都是3,因此节点D的点度中心性最高。整个网络一共有7个节点,意味着每个人最多可以有6个社会关系。因此,节点D的点度中心性是6/6=1,其他节点的点度中心性是3/6=0.5。
中介中心性(betweenness centrality)
网络中两个非相邻成员之间的相互作用依赖于其他成员,特别是两成员之间路径上的那些成员。他们对两个非相邻成员之间的相互作用具有控制和制约作用。Freeman (1979)认为中间成员对路径两端的成员具有“更大的人际关系影响”。因此,中介中心性的思想是:如果一个成员位于其他成员的多条最短路径上,那么该成员就是核心成员,就具有较大的中介中心性。
计算网络中任意两个节点的所有最短路径,如果这些最短路径中很多条都经过了某个节点,那么就认为这个节点的中介中心性高。回到上面的蝴蝶结网络,假设我们要计算节点D的中介中心性。
首先,我们计算节点D之外,所有节点对之间的最短路径有多少条,这里是15条(在6个节点中选择两个节点即节点对的个数)。
然后,我们再看所有这些最短路径中有多少条经过节点D,例如节点A要想找到节点E,必须经过节点D。经过节点D的最短路径有9条。
最后,我们用经过节点D的最短路径除以所有节点对的最短路径总数,这个比率就是节点D的中介中心性。节点D的中介中心性是9/15=0.6。
如果说点度中心性发现的是网络中的“名人”,那么中介中心性的现实意义是什么呢?
Maksim Tsvetovat&Alexander Kouznetsov在《社会网络分析》一书中有两个例子:
- 鲍勃徘徊在两个女人之间,他贪恋爱丽丝的美丽和谈吐,亦无法舍弃卡若琳娜的乐天和无忧无虑。但他必须小心谨慎,生怕自己在其中任何一个人面前露馅,这样的关系充满了压力和焦虑
- 银行家以5%的利率接受A公司的存款,以7%的利率贷款给B公司,这样的关系给银行家带来了巨大的利益。它的前提是,市场中的A公司和B公司不能直接接触,或至少无法轻易地找到对方
鲍勃和银行家的故事尽管截然不同,但他们都处于一种被称为被禁止的三元组(forbidden triad)的关系中,需要确保三元组的末端不能直接联系。没有联系就像网络中出现了一个洞,因此也被称为结构洞。
当网络中众多成员的接触或低成本接触都依赖我时,我就对其他成员有了控制和制约作用。我可以利用这种关系控制信息的流动,套取巨大的利益。当然,这样的关系也充满着压力和紧张。诚如Maksim Tsvetovat&Alexander Kouznetsov所言,商人的成功,不仅取决于他们对不对称信息的利用和经营能力,也需要对创造和维持套利机会带来的压力的高度容忍。
接近中心性(closeness centrality)
点度中心性仅仅利用了网络的局部特征,即节点的连接数有多少,但一个人连接数多,并不代表他/她处于网络的核心位置。接近中心性和中介中心性一样,都利用了整个网络的特征,即一个节点在整个结构中所处的位置。如果节点到图中其他节点的最短距离都很小,那么它的接近中心性就很高。相比中介中心性,接近中心性更接近几何上的中心位置。
假设我们要计算节点D的接近中心性,首先我们计算从节点D到所有其他节点的最短距离。从图中可以判断,节点D到所有其他节点的距离均为1,距离之和为6。因此,节点D的接近中心性为(7-1)/6=1。分子为网络中节点总数减去1。也就是说,如果一个人可以直接跟网络中所有其他人联系,那么他/她的接近中心性就是1。对于其他节点,如节点A的接近中心性为(7-1)/9=0.667。
接近中心性高的节点一般扮演的是八婆的角色(gossiper)。他们不一定是名人,但是乐于在不同的人群之间传递消息。
特征向量中心性(eigenvector centrality)
特征向量中心性的基本思想是,一个节点的中心性是相邻节点中心性的函数。也就是说,与你连接的人越重要,你也就越重要。
特征向量中心性和点度中心性不同,一个点度中心性高即拥有很多连接的节点特征向量中心性不一定高,因为所有的连接者有可能特征向量中心性很低。同理,特征向量中心性高并不意味着它的点度中心性高,它拥有很少但很重要的连接者也可以拥有高特征向量中心性。
考虑下面的图,以及相应的5x5的邻接矩阵(Adjacency Matrix),A。

邻接矩阵的含义是,如果两个节点没有直接连接,记为0,否则记为1。
现在考虑x,一个5x1的向量,向量的值对应图中的每个点。在这种情况下,我们计算的是每个点的点度中心性(degree centrality),即以点的连接数来衡量中心性的高低。
矩阵A乘以这个向量的结果是一个5x1的向量:
A × x = ( − 1 1 1 0 1 − 1 0 0 1 1 − 1 0 1 0 1 − 1 0 0 0 1 ) ( 3 2 3 3 1 ) = ( 0 × 3 + 1 × 2 + 1 × 3 + 1 × 3 + 0 × 1 1 × 3 + 0 × 2 + 1 × 3 + 0 × 3 + 0 × 1 1 × 3 + 1 × 2 + 0 × 3 + 1 × 3 + 0 × 1 1 × 3 + 0 × 2 + 1 × 3 + 0 × 3 + 1 × 1 0 × 3 + 0 × 2 + 1 × 3 + 0 × 3 + 0 × 1 ) = [ 8 6 8 7 3 ] \mathbf{A} \times \mathbf{x}=\left(\begin{array}{cccc}{-1} & {1} & {1} & {0} \\ {1} & {-1} & {0} & {0} \\ {1} & {1} & {-1} & {0} \\ {1} & {0} & {1} & {-1} \\ {0} & {0} & {0} & {1}\end{array}\right)\left(\begin{array}{l}{3} \\ {2} \\ {3} \\ {3} \\ {1}\end{array}\right)=\left(\begin{array}{c}{0 \times 3+1 \times 2+1 \times 3+1 \times 3+0 \times 1} \\ {1 \times 3+0 \times 2+1 \times 3+0 \times 3+0 \times 1} \\ {1 \times 3+1 \times 2+0 \times 3+1 \times 3+0 \times 1} \\ {1 \times 3+0 \times 2+1 \times 3+0 \times 3+1 \times 1} \\ {0 \times 3+0 \times 2+1 \times 3+0 \times 3+0 \times 1}\end{array}\right)=\left[\begin{array}{c}{8} \\ {6} \\{8} \\ {7} \\ {3}\end{array}\right] A×x=⎝⎜⎜⎜⎜⎛−111101−110010−110000−11⎠⎟⎟⎟⎟⎞⎝⎜⎜⎜⎜⎛32331⎠⎟⎟⎟⎟⎞=⎝⎜⎜⎜⎜⎛0×3+1×2+1×3+1×3+0×11×3+0×2+1×3+0×3+0×11×3+1×2+0×3+1×3+0×11×3+0×2+1×3+0×3+1×10×3+0×2+1×3+0×3+0×1⎠⎟⎟⎟⎟⎞=⎣⎢⎢⎢⎢⎡86873⎦⎥⎥⎥⎥⎤
结果向量的第一个元素是用矩阵A的第一行去“获取”每一个与第一个点有连接的点的值(连接数,点度中心性),也就是第2个、第3个和第4个点的值,然后将它们加起来。
换句话说,邻接矩阵做的事情是将相邻节点的求和值重新分配给每个点。这样做的结果就是“扩散了”点度中心性。你的朋友的朋友越多,你的特征向量中心性就越高。

我们继续用矩阵A乘以结果向量。如何理解呢?实际上,我们允许这一中心性数值再次沿着图的边界“扩散”。我们会观察到两个方向上的扩散(点既给予也收获相邻节点)。我们猜测,这一过程最后会达到一个平衡,特定点收获的数量会和它给予相邻节点的数量取得平衡。既然我们仅仅是累加,数值会越来越大,但我们最终会到达一个点,各个节点在整体中的比例会保持稳定。
现在把所有点的数值构成的向量用更一般的形式表示:
[ − 1 1 1 0 1 − 1 0 0 1 1 − 1 0 1 0 1 − 1 0 0 0 1 − ] [ x 1 x 2 x 3 x 4 x 5 ] = [ 0 ⋅ x 1 + 1 ⋅ x 2 + 1 ⋅ x 3 + 1 ⋅ x 4 + 0 ⋅ x 5 1 ⋅ x 1 + 0 ⋅ x 2 + 1 ⋅ x 3 + 0 ⋅ x 4 + 0 ⋅ x 5 1 ⋅ x 1 + 1 ⋅ x 2 + 0 ⋅ x 3 + 1 ⋅ x 4 + 0 ⋅ x 5 1 ⋅ x 1 + 0 ⋅ x 2 + 1 ⋅ x 3 + 0 ⋅ x 4 + 1 ⋅ x 5 0 ⋅ x 1 + 0 ⋅ x 2 + 0 ⋅ x 3 + 1 ⋅ x 4 + 0 ⋅ x 5 ] \left[\begin{array}{ccccc}{-} & {1} & {1} & {1} & {0} \\ {1} & {-} & {1} & {0} & {0} \\ {1} & {1} & {-} & {1} & {0} \\ {1} & {0} & {1} & {-} & {1} \\ {0} & {0} & {0} & {1} & {-}\end{array}\right]\left[\begin{array}{l}{x_{1}} \\ {x_{2}} \\ {x_{3}} \\ {x_{4}} \\ {x_{5}}\end{array}\right]=\left[\begin{array}{c}{0 \cdot x_{1}+1 \cdot x_{2}+1 \cdot x_{3}+1 \cdot x_{4}+0 \cdot x_{5}} \\ {1 \cdot x_{1}+0 \cdot x_{2}+1 \cdot x_{3}+0 \cdot x_{4}+0 \cdot x_{5}} \\ {1 \cdot x_{1}+1 \cdot x_{2}+0 \cdot x_{3}+1 \cdot x_{4}+0 \cdot x_{5}} \\ {1 \cdot x_{1}+0 \cdot x_{2}+1 \cdot x_{3}+0 \cdot x_{4}+1 \cdot x_{5}} \\ {0 \cdot x_{1}+0 \cdot x_{2}+0 \cdot x_{3}+1 \cdot x_{4}+0 \cdot x_{5}}\end{array}\right] ⎣⎢⎢⎢⎢⎡−11101−10011−10101−10001−⎦⎥⎥⎥⎥⎤⎣⎢⎢⎢⎢⎡x1x2x3x4x5⎦⎥⎥⎥⎥⎤=⎣⎢⎢⎢⎢⎡0⋅x1+1⋅x2+1⋅x3+1⋅x4+0⋅x51⋅x1+0⋅x2+1⋅x3+0⋅x4+0⋅x51⋅x1+1⋅x2+0⋅x3+1⋅x4+0⋅x51⋅x1+0⋅x2+1⋅x3+0⋅x4+1⋅x50⋅x1+0⋅x2+0⋅x3+1⋅x4+0⋅x5⎦⎥⎥⎥⎥⎤
我们认为,图中的点存在一个数值集合,对于它,用矩阵A去乘不会改变向量各个数值的相对大小。也就是说,它的数值会变大,但乘以的是同一个因子。用数学符号表示就是:
M x = λ x \mathbf{M} \mathbf{x}=\lambda \mathbf{x} Mx=λx
M × ( x 1 x 2 ⋯ x n ) = ( λ x 1 λ x 2 ⋯ λ x n ) \mathbf{M} \times\left(\begin{array}{c}{x_{1}} \\ {x_{2}} \\ {\cdots} \\ {x_{n}}\end{array}\right)=\left(\begin{array}{c}{\lambda x_{1}} \\ {\lambda x_{2}} \\ {\cdots} \\ {\lambda x_{n}}\end{array}\right) M×⎝⎜⎜⎛x1x2⋯xn⎠⎟⎟⎞=⎝⎜⎜⎛λx1λx2⋯λxn⎠⎟⎟⎞
满足这一属性的向量就是矩阵M的特征向量。特征向量的元素就是图中每个点的特征向量中心性。
特征向量中心性的计算需要读者具备矩阵乘法和特征向量的知识,但不影响这里读者对特征向量中心性思想的理解,不再赘述。
有向图与PageRank
PageRank是衡量有向网络中节点重要性的指标。
我们将万维网抽象成有向图:(1)每个网页抽象成一个节点,假设有A、B、C、D四个节点;(2)用户通过超链接在网页之间跳转,这种跳转是有方向的(directed),从网页A跳转到网页B不代表可以从网页B链接到网页A,这种节点之间的有方向的连接被抽象成有方向的边。整个网络构成一个有向图。

你可以很轻易地找到最受欢迎的网页。但是,PageRank的思想认为,指标最好还需要考虑到指向你的那些网页。也就是说,来自受欢迎的网页的跳转应该重于不太受欢迎的网页的跳转。这就是PageRank思想的精华,Google就是利用这一思想来给网站排名的。这里的思想依据和特征向量中心性其实是一致的。
首先,我们假设用户停留在一个页面时,跳转到每个链接页面的概率是相同的。例如,用户停留在页面A,他可以跳转到B、C、D三个页面,我们假设用户跳转到每个页面的概率相同,也就是说用户跳转到每个页面的概率均为1/3。我们可以用下面的转移矩阵(Transition Matrix)来表示整个有向图的情况:
M = [ 0 1 / 2 0 1 / 2 1 / 3 0 0 1 / 2 1 / 3 1 / 2 0 0 1 / 3 0 1 0 ] M=\left[\begin{array}{cccc}{0} & {1 / 2} & {0} & {1 / 2} \\ {1 / 3} & {0} & {0} & {1 / 2} \\ {1 / 3} & {1 / 2} & {0} & {0} \\ {1 / 3} & {0} & {1} & {0}\end{array}\right] M=⎣⎢⎢⎡01/31/31/31/201/2000011/21/200⎦⎥⎥⎤
假设有向图中有n个节点,那么M就是一个n行n列的矩阵,其中的第i行第j列代表从页面j跳转到页面i的概率。例如,M矩阵的第一行代表从ABCD跳转到页面A的概率。
然后,我们设每个页面的初始rank为1/4,4个页面的初始rank构成向量v:
v = [ 1 / 4 1 / 4 1 / 4 1 / 4 ] v=\left[\begin{array}{c}{1 / 4} \\ {1 / 4} \\ {1 / 4} \\ {1 / 4}\end{array}\right] v=⎣⎢⎢⎡1/41/41/41/4⎦⎥⎥⎤
用M第一行乘以向量v,得到的就是页面A最新rank的合理估计: 0 ∗ 1 / 4 + 1 / 2 ∗ 1 / 4 + 0 ∗ 1 / 4 + 1 / 2 ∗ 1 / 4 = 1 / 4 0*1/4+1/2*1/4+0*1/4+1/2*1/4=1/4 0∗1/4+1/2∗1/4+0∗1/4+1/2∗1/4=1/4。Mv的结果就是ABCD四个页面的新rank:
M v = [ 1 / 4 5 / 24 5 / 24 1 / 3 ] M v=\left[\begin{array}{c}{1 / 4} \\ {5 / 24} \\ {5 / 24} \\ {1 / 3}\end{array}\right] Mv=⎣⎢⎢⎡1/45/245/241/3⎦⎥⎥⎤
然后用M再乘以新的rank向量,又会产生一个新的rank向量。迭代这一过程,Mv结果各个值的相对大小会保持稳定。也就是说,其结果等于用一个标量乘以v。
满足这一属性的向量就是矩阵M的特征向量。这里的结果会收敛在[1/4, 1/4, 1/5, 1/4],这就是A、B、C、D最后的PageRank。这一结果表明,相比于网页C, ABD更为重要。
上述方程式假设上网者一定是通过网页上的链接进行跳转的,但实际上,上网者在每一步都有可能在地址栏随机输入一个网址,跳转到其他页面,而不是点击网页上的链接。或者,上网者可能到达一个没有任何链出页面的网页,这时他会随机到另外的页面进行浏览。
想象有两个网页的简单例子,网页A链接到B,但B无法链接到A。转移矩阵如下:
M = [ 0 0 1 0 ] M=\left[\begin{array}{ll}{0} & {0} \\ {1} & {0}\end{array}\right] M=[0100]
不断迭代,最后我们得到的是一个0矩阵:
M v = [ 0 0 1 0 ] [ 1 2 1 2 ] = [ 0 1 2 ] M v=\left[\begin{array}{ll}{0} & {0} \\ {1} & {0}\end{array}\right]\left[\begin{array}{l}{\frac{1}{2}} \\ {\frac{1}{2}}\end{array}\right]=\left[\begin{array}{l}{0} \\ {\frac{1}{2}}\end{array}\right] Mv=[0100][2121]=[021]
考虑到B比A重要,这一结果是不合理的,它认为A和B同等重要。为了解决这个问题,我们引入 “心灵运输”(Teleportation) 的概念。它意味着上网者每一步都有可能随机输入一个网址(心灵运输),跳转到其他页面(这意味着每一步,网络上的每个网页都有一定的概率被访问到,它的概率为(1-d)/N,即上网者心灵运输的概率乘以每个网页被访问的概率),而不是点击网页上的链接。
我们假设上网者在任何页面继续向下浏览的概率为d=0.85。d也被称为阻尼系数(damping factor)。1-d=0.15就是上网者停止点击,随机跳到新网址的概率,即心灵运输的概率。设网页总数为N,那么跳转到任一网页的概率为N。因此,调整后的方程式如下:
v ′ = d M v + e 1 − d N v^{\prime}=d M v+e \frac{1-d}{N} v′=dMv+eN1−d
其中的e为单位矩阵,这样才能与方程式的前半部分相加。
v ′ = 0.8 × [ 0 0 1 0 ] [ 1 2 1 2 ] + 0.2 × [ 1 2 1 2 ] = [ 1 10 1 2 ] v^{\prime}=0.8 \times\left[\begin{array}{ll}{0} & {0} \\ {1} & {0}\end{array}\right]\left[\begin{array}{l}{\frac{1}{2}} \\ {\frac{1}{2}}\end{array}\right]+0.2 \times\left[\begin{array}{l}{\frac{1}{2}} \\ {\frac{1}{2}}\end{array}\right]=\left[\begin{array}{c}{\frac{1}{10}} \\ {\frac{1}{2}}\end{array}\right] v′=0.8×[0100][2121]+0.2×[2121]=[10121]
不断迭代后,两个网页的rank会收敛为:
[ 1 10 1 2 ] 0.1 0.18 ] ⋯ [ 0.35 0.64 ] \left.\left[\begin{array}{c}{\frac{1}{10}} \\ {\frac{1}{2}}\end{array}\right] \begin{array}{l}{0.1} \\ {0.18}\end{array}\right] \cdots \left[\begin{array}{l}{0.35} \\ {0.64}\end{array}\right] [10121]0.10.18]⋯[0.350.64]
小结
- 点度中心性:一个人的社会关系越多,他/她就越重要
- 中介中心性:如果一个成员处于其他成员的多条最短路径上,那么该成员就是核心成员
- 接近中心性:一个人跟所有其他成员的距离越近,他/她就越重要
- 特征向量中心性:与你连接的人社会关系越多,你就越重要
- PageRank:来自受欢迎的网页的跳转应该重于不太受欢迎的网页的跳转