人工智能导论实验2——野人渡河&黑白棋问题

人工智能导论实验2——野人渡河&黑白棋问题

实验目的及要求：
本项目要求能够理解人工智能的基本原理，理解状态空间的概念、原理和方法，掌握用状态空间表示问题的步骤，掌握搜索方法的基本原理，并能够实际问题给出具体的实现。
实验内容：
1.状态、状态空间、算符、用状态空间表示问题的步骤
2.状态空间、用状态空间求解问题的过程
3.宽度优先搜索、有界深度优先搜索、启发式搜索
4.状态空间法求解实际问题的实现过程

实验项目1：

三名传教士和三名食人族必须使用最多可搭载两个人的船穿越一条河流，这是因为对于两岸，如果在岸上都有传教士，则食人族不能超过他们（如果是的话，食人族会吃掉传教士）。船上没有人时，船不能独自过河。求解一种解决方案，将所有的传教士和食人族运送到对岸。
有N个传教士和N个野人来到河边渡河，河岸有一条船，每次至多可供2人乘渡。问传教士为了安全起见，应如何规划摆渡方案，使得任何时刻，河两岸以及船上的野人数目总是不超过传教士的数目。即求解过程中，任何时刻满足M(传教士数)≥C(野人数)和M+C≤k的摆渡方案。 [source: Wikipedia]

实验要求：
1．形式化表示MC问题：①状态空间②初始状态③行动④转移模型⑤目标⑥路径代价
2. 画出状态图(可知MC=3时，共有15个合法状态)。
3. 根据问题的形式化结果，结合prolog语言的特点，Prolog实现该问题求解；

实验步骤
1.形式化MC问题
①状态空间
用一个三元组[m，c，b]来表示河岸上的状态，其中m、c分别代表某一岸上传教士与野人的数目，b=left表示船在左岸，b=right则表示船在右岸。约束条件是: 两岸上M≥C || M=0 , 船上M+C≤2。
综上，状态空间可表示为：(ML，CL，BL)，其中0≤ML，CL≤N，BL∈{left, right}。
状态空间的总状态数为(N+1)×(N+1)×2

②初始状态
问题的初始状态是(N，N，left)

③行动
该问题主要有两种操作：从左岸划向右岸和从右岸划向左岸，以及每次摆渡的传教士和野人个数。
使用一个2元组（BM，BC）来表示每次摆渡的传教士和野人个数，我们用i代表每次过河的总人数，i =[1,2…k]，则每次有BM个传教士和BC=i-BM个野人过河，其中BM= 0~i，而且当BM!=0时需要满足BM>=BC。则从左到右的操作为：（ML-BM，CL-BC，B = 1），从右到左的操作为：（ML+BM，CL+BC，B = 0）。
例如当N=3，K=2时，满足条件的（BM，BC）有：
从左岸到达右岸：（0,1）、（0,2）、（1,0）、（1,1）、（2,0）
从右岸到达左岸：（0,1）、（0,2）、（1,0）、（1,1）、（2,0）
共10类行动

④转移模型
当前状态+Action构成转移模型

⑤目标
[0,0,0]

⑥路径代价
在搜索过程中的摆渡次数

2.画出状态图(可知MC=3时，共有15个合法状态)。

3.求解问题
初始状态：河左岸有3个野人河3个修道士；河右岸有0个野人和0个修道士；船停在左岸，船上有0个人。
目标状态：河左岸有0个野人和0个修道士；河右岸有3个野人和3个修道士；船停在右岸，船上有0个人。
根据要求，共得出以下5中可能的渡河方案：
　　（1）渡1修道士
　　（2）渡1野人
　　（3）渡2野人
　　（4）渡2修道士
（5）渡1修道士1野人

由题目，得到每次渡河后，某一岸的安全的条件：
（1）修道士人数为0野人数不论
（2）修道士人数大于野人人数，且均大于0

每次船的位置改变，都意味着发生了移动，即两岸有了人数变化
在安全的情况下发生移动，记录有效转移（即在之前未被记录且保证两岸安全的转移），直达开始状态达到目标状态，否则就继续递归。

prolog程序如下：

move(1,0).%列出渡河方式1个修道士0个野人
move(0,1).%列出渡河方式0个修道士1个野人
move(0,2).%列出渡河方式0个修道士2个野人
move(2,0).%2个修道士0个野人
move(1,1).%1个修道士1个野人

safe((X,Y)):-  %某岸安全的条件
    (X=:=0,Y>=0,!);  %条件1修道士人数为0野人数不论
    (X>=Y,X>=0,Y>=0). %条件2修道士人数大于野人人数，且均大于0

allsafe((X,Y,_)):-   % 左右岸都要安全，下划线表示船的状态不关心
    safe(X),
    safe(Y).

if_then_else(Condition,Then,Else) :- %定义if_then_else的执行逻辑，在下面使用
   call(Condition) -> call(Then) ; call(Else).

aftermove((X,Y,Q),Move,Statu):-
    (A,B)=X,
    (C,D)=Y,
    (E,F)=Move,
if_then_else(
%if船的位置要变
        Q=:=0, 
%then对应左岸和右岸人数的改变，船的位置要变
       (C1 is C+E, D1 is D+F, A1 is A-E, B1 is B-F, Statu=((A1,B1),(C1,D1),1)), 
%else
       (C1 is C-E, D1 is D-F, A1 is A+E, B1 is B+F, Statu=((A1,B1),(C1,D1),0))
    ).
valid(Statu,Statu1):- %有效转移
    move(X,Y),
    aftermove(Statu,(X,Y),Statu1),
    allsafe(Statu1).%移动之后要求都是合法的

%记录转移的状态开始A等于表X的第一个元素
first_one(A,X):- append([A],_,X).         
last_part(A,X):- first_one(B,X),append([B],A,X).   %A等于表X的除第一个元素的后部分表
show(L):- %输出
    if_then_else(
        (length(L,X),X>0),
(first_one(A,L),last_part(B,L),write('['),write(A),write(']'),nl,show(B)),
        fail).
yrdh(X,Y,L):-
    if_then_else(
        X=Y, %开始状态到达目标状态就输出否则就继续递归
       (write('================'),nl,show(L),nl),
        (valid(X,Z), not(member(Z,L)),yrdh(Z,Y,[Z|L]))
).

4.实验结果
解决题目上3个修道士、3个野人的问题，输入：
yrdh (((0,0),(3,3),1),((3,3),(0,0),0),[((0,0),(3,3),1)]).
其中，((0,0),(3,3),1)表示初始状态，即
左岸 0个修道士，0个野人
右岸3个修道士，3个野人
船在右岸
((3,3),(0,0),0)表示目标状态，即
左岸3个修道士，3个野人
右岸 0个修道士，0个野人
船在左岸
[((0,0),(3,3),1)]表示输出的最终状态

实验项目2：

黑白棋(reversi),也叫苹果棋，翻转棋，是一个经典的策略性游戏。一般棋子双面为黑白两色，故称“黑白棋”。因为行棋之时将对方棋子翻转，变为己方棋子，故又称“翻转棋”。棋子双面为
红、绿色的成为“苹果棋”。它使用8*8 的棋盘，由两人执黑子和白子轮流下棋，最后子多方为
胜。
游戏规则： 棋局开始时黑棋位于E4 和D5，白棋位于D4 和E5，如下图所示

实验要求：

1. 参考华为《人工智能导论》实验手册，在华为云的ModelArts中用Python实现该问题的求解。

1.游戏规则：
开始时，黑棋位于D5和E4,白棋位于D4和E5。一个合法的落子：
1).在空处落子、并翻转对手一个或多个棋子；
2).新落子位置必须在可以夹住对方的位置上、对方被夹住的棋子翻转。可以是横着夹、竖着夹、对角线夹；
3).任何被夹住的棋子必须被反过来。如果一方没有合法棋步，也就是无论他下在哪里，都无法翻转对方的棋子了，这一轮只能弃权。棋局持续知道棋盘填满或双方都没有合法棋步可下。如果一方落子时间超过1min，或者连续三次落子不合法，则判断该方失败。

2.游戏结束的条件：
（1）整个棋盘满了
（2）一方的棋子已经被对方吃光
（2）两名玩家都没有可以落子的棋盘格
（3）一方落子在非法位置
前3种情况以棋子数目来计算胜负，棋子多的一方获胜;第四种情况判定对方获胜

3.人机对弈流程：
首先，程序询问用户棋盘的大小。接着，程序询问用户“计算机持黑棋还是白棋”。在本程序中，我们用字母’X’代表黑棋， 用字母’O’代表白棋，并且假设总是黑棋玩家先走。
所以，如果计算机持黑棋，计算机就先走; 否则，程序提示人类玩家先走。每走一步，程序输出棋盘。黑白棋玩家轮流下棋，直到一个玩家无符合规则的落子位置。
此时，程序输出信息“O player has no valid move.”(假设白棋玩家无棋可走)，并且提示黑棋玩家继续下棋。
每走一步，程序除输出棋盘外，还要检测游戏是否结束。如果程序检查出游戏结束，输出输赢信息并中止程序。输赢信息可以是: “O player wins.”, “X player wins.” 或者“Draw!”. 如果用户落子非法，程序应检测到并且输出“Invalid move.”， 结束程序，宣布赢家。

python代码如下（一共有4个py文件）：
Migong.py:

# an example for maze using qlearning, two dimension
import numpy as np
# reward matrix R
R = np.array([[-1, -1, -1, -1, 0, -1],
              [-1, -1, -1, 0, -1, 100],
              [-1, -1, -1, 0, -1, -1],
              [-1, 0, 0, -1, 0, -1],
              [0, -1, -1, 0, -1, 100],
              [-1, 0, -1, -1, 0, 100]])

Q = np.zeros((6, 6), float)
gamma = 0.8

episode = 0
while episode < 1000:
     state = np.random.randint(0, 6)
     for action in range(6):
          if R[state, action] > -1:
               Q[state, action] = R[state, action] + gamma*max(Q[action])
     episode = episode + 1

print(Q)

constant.py:

from enum import Enum
class Status(Enum):

    WAIT = 0
    ONGOING = 1
    FOUL = 2
    XWIN = 3
    OWIN = 4
    DRAW = 5

    def __str__(self):
        return str(_STATUS[self.value])

_STATUS = {Status.WAIT.value: 'wait the game to start',
           Status.ONGOING.value: 'in the game',
           Status.FOUL.value: 'someone fouls in the game',
           Status.XWIN.value: 'X player wins!',
           Status.OWIN.value: 'O player wins!',
           Status.DRAW.value: 'DRAW!'}

board.py:

class Board():
    def __init__(self, n):
        self.n = n
        self.board = self.generateBoard()
        self.chess = {0: '.', 1: 'O', 2: 'X'}

    def generateBoard(self):
        """
        生成初始棋盘
        
        Args:
        Returns:
        """

        i = int(self.n / 2)
        board = [[0] * self.n for _ in range(self.n)]
        board[i][i]=board[i-1][i-1] = 1
        board[i][i-1]=board[i-1][i] = 2
        return board

    def draw(self):
        """
        绘出棋盘 

        Args:
        Returns:
        """

        index = 'abcdefghijklmnopqrstuvwxyz'
        print(' ',*index[:self.n])
        for h,row in zip(index,self.board):
            print(h,*map('.OX'.__getitem__,row))
        print()

reversi.py:

#只需运行该文件即可!
from board import Board
import itertools
import operator
import collections
from functools import reduce
from constant import Status
import time
import csv

class Reversi():

    _DIRECTIONS = [(1,0),(1,1),(1,-1),(-1,0),(-1,1),(-1,-1),(0,1),(0,-1)]

    def __init__(self, n, turn):
        self.n = n                                              # board dimension
        self.b = Board(n)                                       # board
        self.turn = 0 if turn == 'X' or turn == 'x' else 1      # player turn
        self.step = 1                                           # game step
        self.status = Status.WAIT                               # game status

    def isValidPosition(self,x,y):
        """检查位置的有效性
        Args:
            x:int
                行坐标
            y:int
                列坐标
        Returns:
            bool:  
        """

        return 0 <= x < self.n and 0 <= y < self.n
    
    def nextPosition(self,direction,x,y):
        """得到这个方向下一步坐标

        Args:
            direction:Tuple(int,int)
                移动的方向
            r:int
                行坐标
            c:int
                列坐标
        Returns:
            int,int:
                下一个位置的行坐标和列坐标
        """

        return x+direction[0],y+direction[1]
    
    def score(self,r,c):
        """得到落子在r,c处时需翻转的棋子坐标的集合
       
        Args:
            r:int
                行坐标
            c:int
                列坐标
        Returns:
            List(Tuple(int,int)):
                落子在r,c处时需翻转的棋子坐标的集合
        """

        return list(itertools.chain.from_iterable([self.scoreDirection(r+m[0],c+m[1],m,self.step%2+1,[]) for m in Reversi._DIRECTIONS]))

    def scoreDirection(self,x,y,direction,color,turn):
        """得到需要翻转的棋子坐标
       
        Args:
            x:int
                行坐标
            y:int
                列坐标
            direction:List(Tuple(int,int))
                移动的方向
            color:int
                落子的棋子颜色
            turn:List(Tuple(int,int))
                需翻转的棋子坐标的集合
        Returns:
            List(Tuple(int,int)):
                需翻转的棋子坐标的集合
        """

        if not self.isValidPosition(x,y) or self.b.board[x][y]==0 :
            return []
        if self.b.board[x][y]!=color:
            turn+=[(x,y)]
            return self.scoreDirection(*self.nextPosition(direction,x,y),direction,color,turn)
        else:
            return turn

    def checkPut(self, pos):
        """检查人落子是否有效
        Args:
            pos:Tuple(int,int)       
        Returns:
        Raises:
            AssertionError: 落子位置无效
        """

        assert len(pos)>=2 , 'move position disable'
        r = ord(pos[0]) - 97
        c = ord(pos[1]) - 97
        assert 0 <= r < self.n and 0 <= c < self.n, 'move position disable'
        turnList = self.score(r, c)
        if turnList:
            for x,y in turnList+[(r,c)]:
                self.b.board[x][y] = self.step % 2+1
            return True
        else:
            return False

    def checkGame(self):
        """检查游戏状态
        Args:
        Returns:
        """
       
        empty,oNum,xNum = operator.itemgetter(0,1,2)(collections.Counter(itertools.chain.from_iterable(self.b.board)))
        hasPut = True
        pos,turnList = self.aiPut()
        if not turnList:
            self.step += 1
            posNext,turnListNext = self.aiPut()
            if not turnListNext:
                hasPut = False
            else:
                self.step -= 1
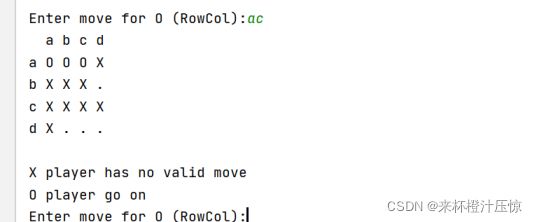
                print('{} player has no valid move'.format(self.b.chess[self.step % 2+1]))
                self.step -= 1
                self.turn -= 1
                print('{} player go on'.format(self.b.chess[self.step % 2+1]))
        if empty ==0 or oNum==0 or xNum == 0 or not hasPut:
            self.status = [Status.DRAW.value,Status.OWIN.value,Status.XWIN.value][(oNum > xNum)-(oNum<xNum)]
    
    def cmp(self,a,b):
        """比较

        Args:
            a:List(Tuple(int,int),List(Tuple(int,int)))
            b:List(Tuple(int,int),List(Tuple(int,int)))
        Returns:
            返回List[1]长度大的，相等则返回行坐标小的，行坐标相等时返回列坐标小的
        """

        if len(a[1])>len(b[1]):
            return a 
        elif len(a[1])==len(b[1]) and a[0]<=b[0]:
            return a
        else:
            return b
          
    def aiPut(self):
        """得到电脑得落子位置和待翻转的棋子坐标集合

        有位置可下时返回最佳落子位置
        没有位置可以下时返回(),[]
        
        Args:
        Returns:
           Tuple(int,int)
            落子位置
           List(Tuple(int,int))
            待翻转的棋子坐标集合
        """

        allPos = filter(lambda pos : self.b.board[pos[0]][pos[1]]==0,itertools.product(range(self.n),repeat=2))
        allScoreForPos  = map(lambda pos: [pos,self.score(pos[0],pos[1])],allPos)
        maxScorePos = reduce(self.cmp,allScoreForPos,[(),[]])
        return maxScorePos[0],maxScorePos[1]

    def aiPlay(self):
        """
        电脑落子逻辑

        Args:
        Returns:
        """

        pos,turnList = self.aiPut()
        if turnList:
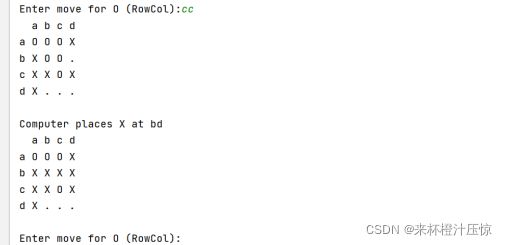
            print('Computer places {} at {}'.format(self.b.chess[self.step % 2+1],chr(pos[0]+97)+chr(pos[1]+97)))
            for x,y in turnList+[pos]:
                self.b.board[x][y] = self.step % 2+1
            reversi.b.draw()
            self.step += 1
            self.turn += 1

    def pPlay(self):
        """
        人落子逻辑

        Args:
        Returns:
        """

        pos = input('Enter move for {} (RowCol):'.format(self.b.chess[self.step % 2+1]))
        if self.checkPut(pos):
            reversi.b.draw()
            self.step += 1
            self.turn += 1
        else:
            print('Invalid move')

    def play(self):
        """
        控制游戏进程

        Args:
        Returns:
        """
        
        self.status = Status.ONGOING
        plays = [self.aiPlay,self.pPlay]
        while self.status == Status.ONGOING:
            plays[self.turn % len(plays)]()
            self.checkGame()
        else:
            print('Game over. {}'.format(Status(self.status)))

    def saveGameToCsv(self,startTime,endTime,turn,filename='Reversi.csv'):
        """
        记录游戏信息保存到csv文件

        Args:
            startTime:float
                游戏开始时间
            endTime:float
                游戏结束时间
            turn:str
                电脑执黑或白
        """
        
        start= time.strftime('%Y%m%d %H:%M:%S',time.localtime(startTime))
        duration = int(endTime - startTime)
        size = f'{self.n}*{self.n}'
        xPlayer,oPlayer = ('Computer','Human') if turn.lower() == 'x' else  ('Human','Computer')
        score = '{} to {}'.format(*operator.itemgetter(2,1)(collections.Counter(itertools.chain.from_iterable(self.b.board))))
        info = [start,duration,size,xPlayer,oPlayer,score]
        with open(f'./{filename}', 'a') as f:
            writer = csv.writer(f)
            writer.writerow(info)
        print(f'history has been saved to {filename}')



if __name__ == "__main__":
    print('Enter the board dimension:')
    try:
        n = int(input())
    except Exception as e:
        print('the board dimension is invalid, start game with default dimension = 4')
        n = 4
    assert 4 <= n <= 26 and n % 2 == 0, 'the board dimension is disable'
    print('Computer plays (X/O):')
    turn = input()
    assert turn in ['X','x','O', 'o'], 'the symbol of computer is disable'
    # generate game
    startTime = time.time()
    reversi = Reversi(n, turn)
    # draw board
    reversi.b.draw()
    reversi.play()
    endTime = time.time()
    # save game info
    reversi.saveGameToCsv(startTime,endTime,turn)
    input('Enter to quit')

实验结果：
（选用4 * 4棋格为了便于展示，也可以选用8 * 8的）

接下来我们就与人机对战对战！（作者自身水平有限！）
①

②

③

④

⑤

⑥

⑦

可以看出在4*4棋盘中，人机赢了！
查看csv文件：

思考题：
1.请简要描述下蒙特卡洛搜索树的主要核心思想？
蒙特卡罗树搜索大概可以被分成四步。选择，拓展，模拟，反向传播。在开始阶段，搜索树只有一个节点，也就是我们需要决策的局面。搜索树中的每一个节点包含了三个基本信息：代表的局面，被访问的次数，累计评分。

（1）选择
在选择阶段，需要从根节点，也就是要做决策的局面R出发向下选择出一个最急迫需要被拓展的节点N，局面R是是每一次迭代中第一个被检查的节点；对于被检查的局面而言，可能有三种可能：
1.该节点所有可行动作都已经被拓展过
2.该节点有可行动作还未被拓展过
3.这个节点游戏已经结束了(例如已经连成五子的五子棋局面)
对于这三种可能：
1.如果所有可行动作都已经被拓展过了，那么将使用UCB公式计算该节点所有子节点的UCB值，并找到值最大的一个子节点继续检查。反复向下迭代。
2.如果被检查的局面依然存在没有被拓展的子节点，那么认为这个节点就是本次迭代的的目标节点N，并找出N还未被拓展的动作A。执行步骤[2]
3.如果被检查到的节点是一个游戏已经结束的节点。那么从该节点直接执行步骤{4]。
每一个被检查的节点的被访问次数在这个阶段都会自增。在反复的迭代之后，我们将在搜索树的底端找到一个节点，来继续后面的步骤。
（2）扩展
在选择阶段结束时候，查找到了一个最迫切被拓展的节点N，以及他一个尚未拓展的动作A。在搜索树中创建一个新的节点Nn作为N的一个新子节点。Nn的局面就是节点N在执行了动作A之后的局面。
（3）模拟
为了让Nn得到一个初始的评分。从Nn开始，让游戏随机进行，直到得到一个游戏结局，这个结局将作为Nn的初始评分。一般使用胜利/失败来作为评分，只有1或者0。
（4）反向传播
在Nn的模拟结束之后，它的父节点N以及从根节点到N的路径上的所有节点都会根据本次模拟的结果来添加自己的累计评分。如果在[1]的选择中直接发现了一个游戏结局的话，根据该结局来更新评分。每一次迭代都会拓展搜索树，随着迭代次数的增加，搜索树的规模也不断增加。当到了一定的迭代次数或者时间之后结束，选择根节点下最好的子节点作为本次决策的结果。

2.请简要描述下博弈树搜索的主要核心思想？
在博弈过程中, 任何一方都希望自己取得胜利。因此,当某一方当前有多个行动方案可供选择时, 他总是挑选对自己最为有利而对对方最为不利的那个行动方案。 此时,如果我们站在A方的立场上,则可供A方选择的若干行动方案之间是“或”关系, 因为主动权操在A方手里,他或者选择这个行动方案, 或者选择另一个行动方案, 完全由A方自己决定。当A方选取任一方案走了一步后,B方也有若干个可供选择的行动方案, 此时这些行动方案对A方来说它们之间则是“与”关系,因为这时主动权操在B方手里,这些可供选择的行动方案中的任何一个都可能被B方选中, A方必须应付每一种情况的发生。
这样,如果站在某一方(如A方,即在A要取胜的意义下), 把上述博弈过程用图表示出来, 则得到的是一棵“与或树”。 描述博弈过程的与或树称为博弈树,它有如下特点：
(1)博弈的初始格局是初始节点。
(2)在博弈树中, “或”节点和“与”节点是逐层交替出现的。自己一方扩展的节点之间是“或”关系, 对方扩展的节点之间是“与”关系。双方轮流地扩展节点。
(3)所有自己一方获胜的终局都是本原问题, 相应的节点是可解节点；所有使对方获胜的终局都是不可解节点。
在二人博弈问题中,为了从众多可供选择的行动方案中选出一个对自己最为有利的行动方案, 就需要对当前的情况以及将要发生的情况进行分析,从中选出最优的走步。最常使用的分析方法是极小极大分析法。 其基本思想是：
(1)设博弈的双方中一方为A,另一方为B。然后为其中的一方(例如A)寻找一个最优行动方案。
(2)为了找到当前的最优行动方案, 需要对各个可能的方案所产生的后果进行比较。具体地说, 就是要考虑每一方案实施后对方可能采取的所有行动, 并计算可能的得分。
(3)为计算得分,需要根据问题的特性信息定义一个估价函数, 用来估算当前博弈树端节点的得分。此时估算出来的得分称为静态估值。
(4)当端节点的估值计算出来后, 再推算出父节点的得分, 推算的方法是：对“或”节点, 选其子节点中一个最大的得分作为父节点的得分,这是为了使自己在可供选择的方案中选一个对自己最有利的方案；对“与”节点, 选其子节点中一个最小的得分作为父节点的得分,这是为了立足于最坏的情况。这样计算出的父节点的得分称为倒推值。
(5)如果一个行动方案能获得较大的倒推值, 则它就是当前最好的行动方案。