Python Fitter 判断数据样本的分布函数拟合

github项目：https://github.com/cokelaer/fitter

fittle 说明文档：
https://fitter.readthedocs.io/en/latest/references.html#

安装fitter

pip install fitter

生成一段模拟数据

from scipy import stats
data = stats.gamma.rvs(2, loc=1.5, scale=2, size=100000)

利用fitter拟合数据样本的分布

from fitter import Fitter
# may take some time since by default, all distributions are tried
# but you call manually provide a smaller set of distributions
f = Fitter(data, distributions=['gamma', 'rayleigh', 'uniform'])
f.fit()
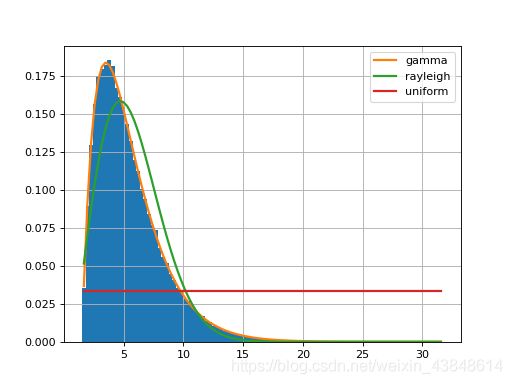
f.summary()

以上输出为拟合的误差与拟合的概率密度曲线及数据的直方图。

Fitter方法参数详解

Fitter(data, xmin=None, xmax=None, bins=100, distributions=None, verbose=True, timeout=10)

参数：
data (list) –输入的样本数据；
xmin (float) – 如果为None，则使用数据最小值，否则将忽略小于xmin的数据；
xmax (float) – 如果为None，则使用数据最大值，否则将忽略大于xmin的数据；
bins (int) – 累积直方图的组数，默认=100；
distributions (list) – 给出要查看的分布列表。 如果没有，则尝试所有的scipy分布(80种),常用的分布distributions=[‘norm’,‘t’,‘laplace’,‘cauchy’, ‘chi2’,’ expon’, ‘exponpow’, ‘gamma’,’ lognorm’, ‘uniform’]；
verbose (bool) –
timeout – 给定拟合分布的最长时间，（默认=10s） 如果达到超时，则跳过该分布。
Fitter返回

f.summary() #返回排序好的分布拟合质量（拟合效果从好到坏）,并绘制数据分布和Nbest分布
f.df_errors #返回这些分布的拟合质量（均方根误差的和）
f.fitted_param #返回拟合分布的参数
f.fitted_pdf #使用最适合数据分布的分布参数生成的概率密度
f.get_best(method='sumsquare_error') #返回最佳拟合分布及其参数
f.hist() #绘制组数=bins的标准化直方图
f.plot_pdf(names=None, Nbest=3, lw=2) #绘制分布的概率密度函数 

一旦执行了拟合，就可能想要获得与最佳分布相对应的参数。参数存储在中fitted_param。例如，在上面的示例中，摘要告诉我们Gamma分布最适合。您将按以下方式检索Gamma分布的参数：

>>> f.fitted_param['gamma']
(1.9870244799532322, 1.5026555566189543, 2.0174462493492964)

在这里，您将需要查看scipy文档以找出那些参数（均值，sigma，shape等）。为了方便起见，我们提供相应的PDF：

f.fitted_pdf['gamma']

但您可能想自己绘制伽马分布。在这种情况下，您将需要使用Scipy软件包本身。这是一个例子

from pylab import linspace, plot
import scipy.stats

dist = scipy.stats.gamma
param = (1.9870, 1.5026, 2.0174)
X = linspace(0,10, 10)
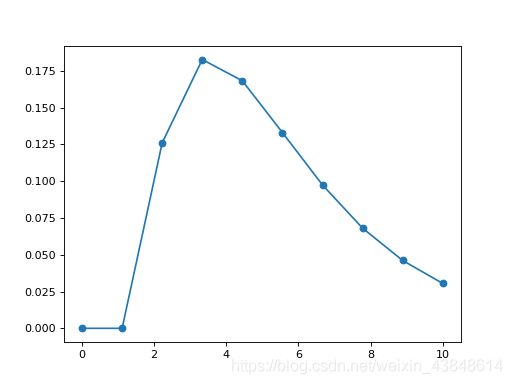
pdf_fitted = dist.pdf(X, *param)
plot(X, pdf_fitted, 'o-')

https://www.freesion.com/article/9309375330/

HistFit类：适合密度函数本身

有时，您只有发行版本身。例如：

import scipy.stats
data = [scipy.stats.norm.rvs(2,3.4) for x in  range(10000)]
Y, X, _ = hist(data, bins=30)

在这里，我们只能访问Y（和X）。

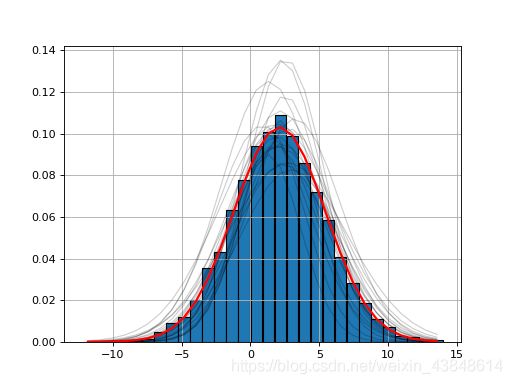
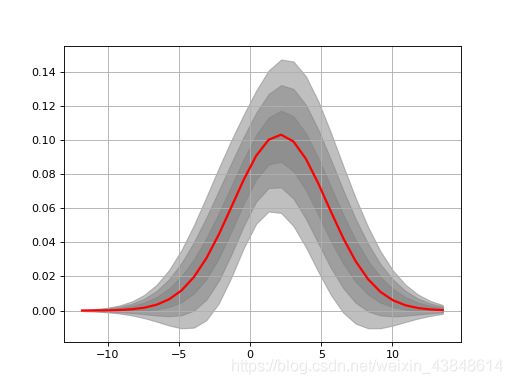
histfit模块提供了HistFit类，可基于多次尝试对X / Y数据进行拟合而在数据集上存在一些错误，从而使用拟合曲线生成数据图。例如，在下面的示例中，我们引入3％的错误，并拟合20次数据以查看拟合是否有意义。

Python拟合数据样本的分布

# Python拟合数据样本的分布
# 安装fitter
# pip install fitter
# 生成一段模拟数据
from scipy import stats
import numpy as np
# N(0,2)+N(0,10)
data1 = list(stats.norm.rvs(loc=0, scale=2, size=70000))
data2 = list(stats.norm.rvs(loc=0, scale=20, size=30000))
data = np.array(data1+data2)
 
# 利用fitter拟合数据样本的分布
from fitter import Fitter
# may take some time since by default, all distributions are tried
# but you call manually provide a smaller set of distributions
f = Fitter(data, distributions=['norm', 't', 'laplace', 'rayleigh'])
f.fit()
f.summary() #返回排序好的分布拟合质量（拟合效果从好到坏）,并绘制数据分布和Nbest分布
f.df_errors #返回这些分布的拟合质量（均方根误差的和）
f.fitted_param #返回拟合分布的参数
f.fitted_pdf #使用最适合数据分布的分布参数生成的概率密度
print(f.get_best(method='sumsquare_error')) #返回最佳拟合分布及其参数
f.hist() #绘制组数=bins的标准化直方图
f.plot_pdf(names=None, Nbest=3, lw=2) #绘制分布的概率密度函数
print(f.summary())
 
# 方法详解
# Fitter方法
# Fitter(data, xmin=None, xmax=None, bins=100, distributions=None, verbose=True, timeout=10)
# 参数：
# data (list) –输入的样本数据；
# xmin (float) – 如果为None，则使用数据最小值，否则将忽略小于xmin的数据；
# xmax (float) – 如果为None，则使用数据最大值，否则将忽略大于xmin的数据；
# bins (int) – 累积直方图的组数，默认=100；
# distributions (list) – 给出要查看的分布列表。 如果没有，则尝试所有的scipy分布(80种),常用的分布distributions=[‘norm’,‘t’,‘laplace’,‘cauchy’, ‘chi2’,’ expon’, ‘exponpow’, ‘gamma’,’ lognorm’, ‘uniform’]；
# verbose (bool) –
# timeout – 给定拟合分布的最长时间，（默认=10s） 如果达到超时，则跳过该分布。
 
# Fitter返回
# f.summary() #返回排序好的分布拟合质量（拟合效果从好到坏）,并绘制数据分布和Nbest分布
# f.df_errors #返回这些分布的拟合质量（均方根误差的和）
# f.fitted_param #返回拟合分布的参数
# f.fitted_pdf #使用最适合数据分布的分布参数生成的概率密度
# f.get_best(method='sumsquare_error') #返回最佳拟合分布及其参数
# f.hist() #绘制组数=bins的标准化直方图
# f.plot_pdf(names=None, Nbest=3, lw=2) #绘制分布的概率密度函数
 
# from fitter import Fitter
# import numpy as np
#
# arr = np.arange(1, 200)
# np.random.shuffle(arr)  # arr为创建的随机数
#
# fitter_dis = Fitter(arr)
# fitter_dis.fit()
# distribution_df = fitter_dis.summary()  # 这里可以得到error最小的Dataframe型数据