聚类算法及其应用

1. 聚类算法都是无监督学习吗?

什么是聚类算法？聚类是一种机器学习技术，它涉及到数据点的分组。给定一组数据点，我们可以使用聚类算法将每个数据点划分为一个特定的组。理论上，同一组中的数据点应该具有相似的属性和/或特征，而不同组中的数据点应该具有高度不同的属性和/或特征。聚类是一种无监督学习的方法，是许多领域中常用的统计数据分析技术。

常用的算法包括K-MEANS、高斯混合模型（Gaussian Mixed Model，GMM）、自组织映射神经网络（Self-Organizing Map，SOM）

2. k-means(k均值)算法

2.1 算法过程

K-均值是最普及的聚类算法，算法接受一个未标记的数据集，然后将数据聚类成不同的组。
K-均值是一个迭代算法，假设我们想要将数据聚类成 n 个组，其方法为:

• 首先选择个随机的点，称为聚类中心（cluster centroids）；
• 对于数据集中的每一个数据，按照距离个中心点的距离，将其与距离最近的中心点关联起来，与同一个中心点关联的所有点聚成一类。
• 计算每一个组的平均值，将该组所关联的中心点移动到平均值的位置。
• 重复步骤，直至中心点不再变化。
  用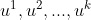 来表示聚类中心，用(1),(2),…,()来存储与第个实例数据最近的聚类中心的索引，K-均值算法的伪代码如下：

Repeat {
    for i = 1 to m
    c(i) := index (form 1 to K) of cluster centroid closest to x(i)
    for k = 1 to K
    μk := average (mean) of points assigned to cluster k
}

算法分为两个步骤，第一个 for 循环是赋值步骤，即：对于每一个样例，计算其应该属于的类。第二个 for 循环是聚类中心的移动，即：对于每一个类，重新计算该类的质心。

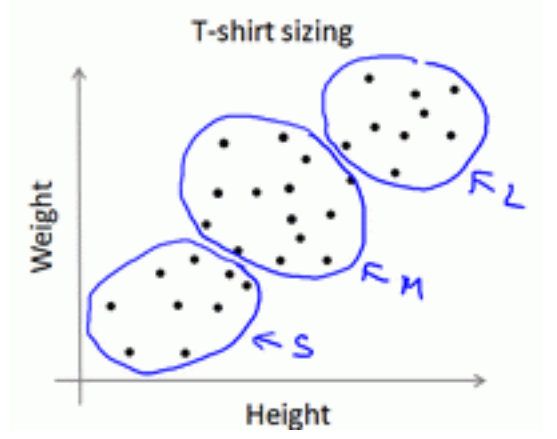
K-均值算法也可以很便利地用于将数据分为许多不同组，即使在没有非常明显区分的组群的情况下也可以。下图所示的数据集包含身高和体重两项特征构成的，利用 K-均值算法将数据分为三类，用于帮助确定将要生产的 T-恤衫的三种尺寸。

2.2 损失函数

K-均值最小化问题，是要最小化所有的数据点与其所关联的聚类中心点之间的距离之和，因此 K-均值的代价函数（又称畸变函数 Distortion function）为：

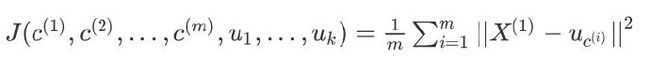
2.3 k值的选择

在运行 K-均值算法的之前，我们首先要随机初始化所有的聚类中心点，下面介绍怎样做：

1. 我们应该选择 < ，即聚类中心点的个数要小于所有训练集实例的数量。
2. 随机选择个训练实例，然后令个聚类中心分别与这个训练实例相等K-均值的一个问题在于，它有可能会停留在一个局部最小值处，而这取决于初始化的情况。

为了解决这个问题，我们通常需要多次运行 K-均值算法，每一次都重新进行随机初始化，最后再比较多次运行 K-均值的结果，选择代价函数最小的结果。这种方法在较小的时候（2–10）还是可行的，但是如果较大，这么做也可能不会有明显地改善。

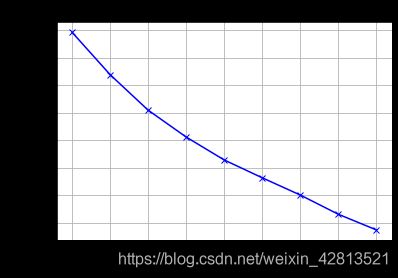
没有所谓最好的选择聚类数的方法，通常是需要根据不同的问题，人工进行选择的。选择的时候思考我们运用 K-均值算法聚类的动机是什么。有一个可能会谈及的方法叫作**“肘部法则”**。关 于“肘部法则”，我们所需要做的是改变值，也就是聚类类别数目的总数。我们用一个聚类来运行 K 均值聚类方法。这就意味着，所有的数据都会分到一个聚类里，然后计算成本函数或者计算畸变函数。代表聚类数字。

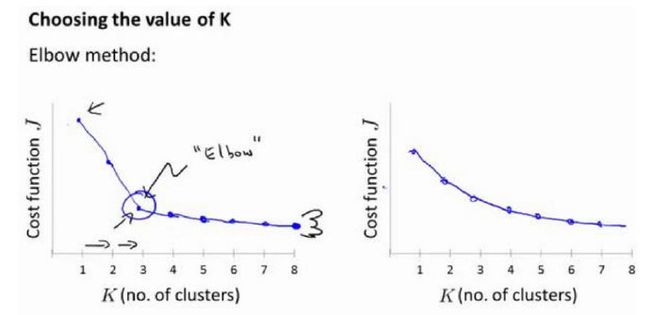
我们可能会得到一条类似于这样的曲线。像一个人的肘部。这就是“肘部法则”所做的，让我们来看这样一个图，看起来就好像有一个很清楚的肘在那儿。你会发现这种模式，它的畸变值会迅速下降，从 1 到 2，从 2 到 3 之后，你会在 3 的时候达到一个肘点。在此之后，畸变值就下降的非常慢，看起来就像使用 3 个聚类来进行聚类是正确的，**这是因为那个点是曲线的肘点，畸变值下降得很快， = 3之后就下降得很慢，那么我们就选 = 3。**当你应用“肘部法则”的时候，如果你得到了一个像上面这样的图，那么这将是一种用来选择聚类个数的合理方法。

2.4 KNN与K-means区别？

K最近邻(k-Nearest Neighbor，KNN)分类算法，是一个理论上比较成熟的方法，也是最简单的机器学习算法之一。
KNN：
1.KNN是分类算法
2.属于监督学习
3.训练数据集是带label的数据
4.没有明显的前期训练过程，属于memory based learning
5.K的含义：一个样本x，对它进行分类，就从训练数据集中，在x附近找离它最近的K个数据点，这K个数据点，类别c占的个数最多，就把x的label设为c。
K-Means
1.K-Means是聚类算法
2.属于非监督学习
3.训练数据集是无label的数据，是杂乱无章的，经过聚类后变得有序，先无序，后有序。
4.有明显的前期训练过程
5.K的含义：K是人工固定好的数字，假设数据集合可以分为K个蔟，那么就利用训练数据来训练出这K个分类。
相似点
都包含这样的过程，给定一个点，在数据集中找离它最近的点。即二者都用到了NN(Nears Neighbor)算法思想。

2.5 K-Means优缺点及改进

k-means：在大数据的条件下，会耗费大量的时间和内存。 优化k-means的建议：

1. 减少聚类的数目K。因为，每个样本都要跟类中心计算距离。

2. 减少样本的特征维度。比如说，通过PCA等进行降维。

3. 考察其他的聚类算法，通过选取toy数据，去测试不同聚类算法的性能。

4. hadoop集群，K-means算法是很容易进行并行计算的。

5. 算法可能找到局部最优的聚类，而不是全局最优的聚类。使用改进的二分k-means算法。

   二分k-means算法：首先将整个数据集看成一个簇，然后进行一次k-means（k=2）算法将该簇一分为二，并计算每个簇的误差平方和，选择平方和最大的簇迭代上述过程再次一分为二，直至簇数达到用户指定的k为止，此时可以达到的全局最优。

3. 高斯混合模型(GMM)

3.1 GMM的思想

高斯混合模型（Gaussian Mixed Model，GMM）也是一种常见的聚类算法，与K均值算法类似，同样使用了EM算法进行迭代计算。高斯混合模型假设每个簇的数据都是符合高斯分布（又叫正态分布）的，当前数据呈现的分布就是各个簇的高斯分布叠加在一起的结果。

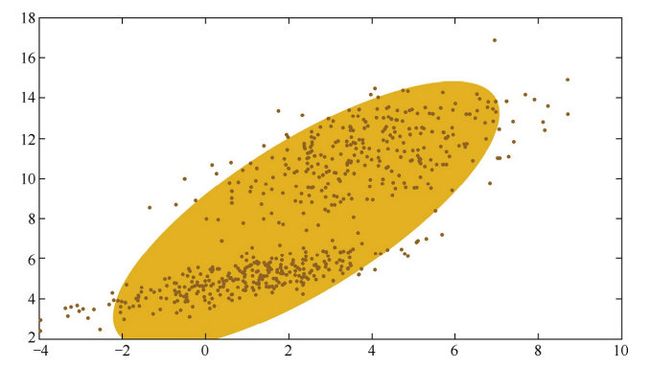
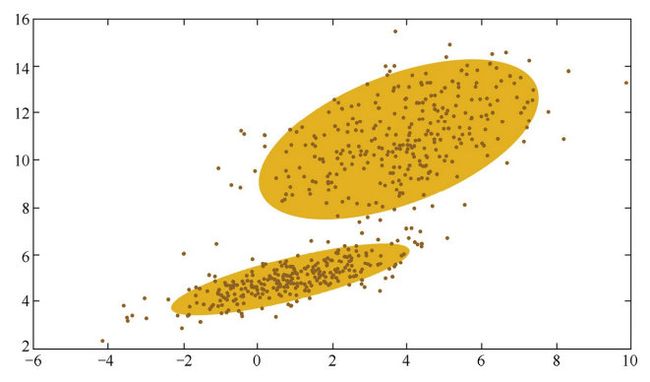
第一张图是一个数据分布的样例，如果只用一个高斯分布来拟合图中的数据，图 中所示的椭圆即为高斯分布的二倍标准差所对应的椭圆。直观来说，图中的数据 明显分为两簇，因此只用一个高斯分布来拟和是不太合理的，需要推广到用多个 高斯分布的叠加来对数据进行拟合。第二张图是用两个高斯分布的叠加来拟合得到的结果。**这就引出了高斯混合模型，即用多个高斯分布函数的线形组合来对数据分布进行拟合。**理论上，高斯混合模型可以拟合出任意类型的分布。


高斯混合模型的核心思想是，假设数据可以看作从多个高斯分布中生成出来 的。在该假设下，每个单独的分模型都是标准高斯模型，其均值 u_i和方差 sum_i是待估计的参数。此外，每个分模型都还有一个参数 pi，可以理解为权重或生成数据的概 率。高斯混合模型的公式为：

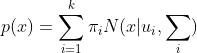
通常我们并不能直接得到高斯混合模型的参数，而是观察到了一系列 数据点，给出一个类别的数量K后，希望求得最佳的K个高斯分模型。因此，高斯 混合模型的计算，便成了最佳的均值μ，方差Σ、权重π的寻找，这类问题通常通过 最大似然估计来求解。遗憾的是，此问题中直接使用最大似然估计，得到的是一 个复杂的非凸函数，目标函数是和的对数，难以展开和对其求偏导。

在这种情况下，可以用EM算法EM算法是在最大化目标函数时，先固定一个变量使整体函数变为凸优化函数，求导得到最值，然后利用最优参数更新被固定的变量，进入下一个循环。具体到高 斯混合模型的求解，EM算法的迭代过程如下。

首先，初始随机选择各参数的值。然后，重复下述两步，直到收敛。

• E步骤。根据当前的参数，计算每个点由某个分模型生成的概率。
• M步骤。使用E步骤估计出的概率，来改进每个分模型的均值，方差和权重。
  高斯混合模型是一个生成式模型。可以这样理解数据的生成过程，假设一个最简单的情况，即只有两个一维标准高斯分布的分模型N(0,1)和N(5,1)，其权重分别为0.7和0.3。那么，在生成第一个数据点时，先按照权重的比例，随机选择一个分布，比如选择第一个高斯分布，接着从N(0,1)中生成一个点，如−0.5，便是第一个数据点。在生成第二个数据点时，随机选择到第二个高斯分布N(5,1)，生成了第二个点4.7。如此循环执行，便生成出了所有的数据点。

也就是说，我们并不知道最佳的K个高斯分布的各自3个参数，也不知道每个 数据点究竟是哪个高斯分布生成的。所以每次循环时，先固定当前的高斯分布不 变，获得每个数据点由各个高斯分布生成的概率。然后固定该生成概率不变，根据数据点和生成概率，获得一个组更佳的高斯分布。循环往复，直到参数的不再变化，或者变化非常小时，便得到了比较合理的一组高斯分布。

3.2 GMM与K-Means相比

高斯混合模型与K均值算法的相同点是：

• 它们都是可用于聚类的算法；
• 都需要 指定K值；
• 都是使用EM算法来求解；
• 都往往只能收敛于局部最优。

而它相比于K 均值算法的优点是，可以给出一个样本属于某类的概率是多少；不仅仅可以用于聚类，还可以用于概率密度的估计；并且可以用于生成新的样本点。

4. 聚类算法如何评估

由于数据以及需求的多样性，没有一种算法能够适用于所有的数据类型、数 据簇或应用场景，似乎每种情况都可能需要一种不同的评估方法或度量标准。例 如，K均值聚类可以用误差平方和来评估，但是基于密度的数据簇可能不是球形， 误差平方和则会失效。在许多情况下，判断聚类算法结果的好坏强烈依赖于主观 解释。尽管如此，聚类算法的评估还是必需的，它是聚类分析中十分重要的部分之一。

聚类评估的任务是估计在数据集上进行聚类的可行性，以及聚类方法产生结 果的质量。这一过程又分为三个子任务。

1. 估计聚类趋势。

   这一步骤是检测数据分布中是否存在非随机的簇结构。如果数据是基本随机 的，那么聚类的结果也是毫无意义的。我们可以观察聚类误差是否随聚类类别数 量的增加而单调变化，如果数据是基本随机的，即不存在非随机簇结构，那么聚 类误差随聚类类别数量增加而变化的幅度应该较不显著，并且也找不到一个合适 的K对应数据的真实簇数。

2. 判定数据簇数。

   确定聚类趋势之后，我们需要找到与真实数据分布最为吻合的簇数，据此判定聚类结果的质量。数据簇数的判定方法有很多，例如手肘法和Gap Statistic方 法。需要说明的是，用于评估的最佳数据簇数可能与程序输出的簇数是不同的。 例如，有些聚类算法可以自动地确定数据的簇数，但可能与我们通过其他方法确 定的最优数据簇数有所差别。

3. 测定聚类质量。

   在无监督的情况下，我们可以通过考察簇的分离情况和簇的紧 凑情况来评估聚类的效果。定义评估指标可以展现面试者实际解决和分析问题的 能力。事实上测量指标可以有很多种，以下列出了几种常用的度量指标，更多的 指标可以阅读相关文献。

   轮廓系数、均方根标准偏差、R方（R-Square）、改进的HubertΓ统计。

Demo

import os
import sys as sys
#reload(sys)
#sys.setdefaultencoding('utf-8')
from sklearn.cluster import KMeans
from sklearn import feature_extraction
from sklearn.feature_extraction.text import TfidfTransformer
from sklearn.feature_extraction.text import CountVectorizer

import matplotlib.pyplot as plt 
from matplotlib.font_manager import FontProperties 
from sklearn.cluster import KMeans 
from scipy.spatial.distance import cdist 
import numpy as np

def tfidf_vector(corpus_path):
    corpus_train=[]
    #利用train-corpus提取特征
    target_train=[]
    for line in open(corpus_path):
        line=line.strip().split('\t')
        if len(line)==2:
            words=line[1]
            category=line[0]
            target_train.append(category)
            corpus_train.append(words)
    print ("build train-corpus done!!")
    count_v1= CountVectorizer(max_df=0.4,min_df=0.01)
    counts_train = count_v1.fit_transform(corpus_train)  
    
    word_dict={}
    for index,word in enumerate(count_v1.get_feature_names()):
        word_dict[index]=word
    
    print ("the shape of train is ")
    print (repr(counts_train.shape))
    tfidftransformer = TfidfTransformer()
    tfidf_train = tfidftransformer.fit(counts_train).transform(counts_train)
    return tfidf_train,word_dict

def cluster_kmeans(tfidf_train,word_dict,cluster_docs,cluster_keywords,num_clusters):#K均值分类
    f_docs=open(cluster_docs,'w+')
    km = KMeans(n_clusters=num_clusters)
    km.fit(tfidf_train)
    clusters = km.labels_.tolist()
    cluster_dict={}
    order_centroids = km.cluster_centers_.argsort()[:, ::-1]      
    doc=1
    for cluster in clusters:
        f_docs.write(str(str(doc))+','+str(cluster)+'\n')
        doc+=1
        if cluster not in cluster_dict:
            cluster_dict[cluster]=1
        else:
            cluster_dict[cluster]+=1
    f_docs.close()
    cluster=1
    
    f_clusterwords = open(cluster_keywords,'w+')
    for ind in order_centroids: # 每个聚类选 50 个词
        words=[]
        for index in ind[:50]:
            words.append(word_dict[index])
        print (cluster),(','.join(words))
        f_clusterwords.write(str(cluster)+'\t'+','.join(words)+'\n')
        cluster+=1
        print ('*****'*5)
    f_clusterwords.close()

def best_kmeans(tfidf_matrix,word_dict):  
    K = range(1, 10) 
    meandistortions = [] 
    for k in K: 
        print (k),('****'*5)
        kmeans = KMeans(n_clusters=k) 
        kmeans.fit(tfidf_matrix)    
        meandistortions.append(sum(np.min(cdist(tfidf_matrix.toarray(), kmeans.cluster_centers_, 'euclidean'), axis=1)) / tfidf_matrix.shape[0]) 
    plt.plot(K, meandistortions, 'bx-')
    plt.grid(True) 
    plt.xlabel('Number of clusters') 
    plt.ylabel('Average within-cluster sum of squares') 
    plt.title('Elbow for Kmeans clustering')
    plt.show()

corpus_train = "corpus_train.txt"
cluster_docs = "cluster_result_document.txt"
cluster_keywords = "cluster_result_keyword.txt"
num_clusters = 7
tfidf_train,word_dict=tfidf_vector(corpus_train)
best_kmeans(tfidf_train,word_dict)
cluster_kmeans(tfidf_train,word_dict,cluster_docs,cluster_keywords,num_clusters)

模拟两个正态分布的参数

from numpy import *
import numpy as np
import random
import copy
import matplotlib.pyplot as plt
import math
import matplotlib.mlab as mlab

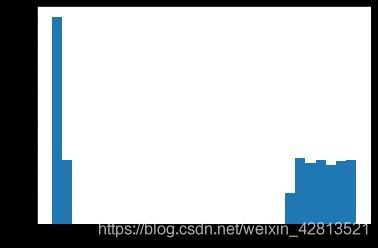
均值不同的样本

EPS = 0.0001
def generate_data():	
	mu1 = 2
	mu2 = 6
	sigma1 = 0.1
	sigma2 = 0.5
	alpha1 = 0.4
	alpha2 = 0.6
	N = 5000
	N1 = int(alpha1 * N)
	X = mat(zeros((N,1)))
	for i in range(N1):
		u1 = random.uniform(-1,1)
		X[i] = u1 * sigma1 + mu1
	for i in range(N-N1):
		u1 = random.uniform(-1,1)
		X[i+N1] = u1 * sigma2 + mu2
	return X

EM算法

def GMM(X):
	k = 2
	N = len(X)
	mu = np.random.rand(k,1)
	print (str('init mu='))
	print (mu)
	Posterior = mat(zeros((N,k)))	
	sigma = np.random.rand(k,1)
	print (str('init sigma='))
	print (sigma)
	alpha = np.random.rand(k,1)
	dominator = 0
	numerator = 0
	print (str('init alpha='))
	print (alpha)
	#先求后验概率
	#print (sigma)
	for it in range(1000):
		for i in range(N):
			dominator = 0
			for j in range(k):
				dominator = dominator + np.exp(-1.0/(2.0*sigma[j]) * (X[i] - mu[j])**2)
				#print -1.0/(2.0*sigma[j]),(X[i] - mu[j])**2,-1.0/(2.0*sigma[j]) * (X[i] - mu[j])**2,np.exp(-1.0/(2.0*sigma[j]) * (X[i] - mu[j])**2)
				#return
			for j in range(k):
				numerator = np.exp(-1.0/(2.0*sigma[j]) * (X[i] - mu[j])**2)
				Posterior[i,j] = numerator/dominator			
		oldmu = copy.deepcopy(mu)
		oldalpha = copy.deepcopy(alpha)
		oldsigma = copy.deepcopy(sigma)
		#最大化	
		for j in range(k):
			numerator = 0
			dominator = 0
			for i in range(N):
				numerator = numerator + Posterior[i,j] * X[i]
				dominator = dominator + Posterior[i,j]
			mu[j] = numerator/dominator
			alpha[j] = dominator/N
			tmp = 0
			for i in range(N):
				tmp = tmp + Posterior[i,j] * (X[i] - mu[j])**2
				#print tmp,Posterior[i,j],(X[i] - mu[j])**2 
			sigma[j] = tmp/dominator
			#print (tmp)
			#print (dominator)
			#print (sigma[j])
		if ((abs(mu - oldmu)).sum() < EPS) and \
			((abs(alpha - oldalpha)).sum() < EPS) and \
			((abs(sigma - oldsigma)).sum() < EPS):
				print (str('final mu=')) 
				print (str(mu))
				print (str('final sigma='))
				print (str(sigma))
				print (str('final alpha='))
				print (str(alpha))
				print (it)
				break

X = generate_data()
plt.hist(X, 30, normed=True)
plt.show()
GMM(X)