Photometric Stereo 光度立体三维重建（三）——由法向量恢复深度（二）DGP方法

在这篇文章中，笔者将介绍一篇论文，论文提出了一种由法向量恢复深度的方法：论文为Surface-from-gradients: An approach based on discrete geometry processing

1.论文的动机与概况

SfS(surface from shading)和PS(photometric stereo)可以计算稠密带噪的法向量图（梯度场），通过积分可计算出深度图。数学上，由三维表面生成的梯度场是可积的，但实际上，由于噪声导致不可积。以前的处理方法中，有强制可积性约束（但会扰乱法向量），也有通过平滑表面来抑制噪声的，但它会把尖锐特征平滑掉。在本文中，通过离散化来避免可积性问题，提出新的表面重建思路。具体来说，重建的表面由一个包含很多面片(facet)的mesh模型M来计算，每个面片对应法向量图（梯度场）的一个样本。在将样本梯度转换到面片的法向量后，使用离散几何方法(DGP)对M进行变形，让其面片符合要求的法向量。M的变形通过迭代计算进行，在每次迭代中，先进行局部成型(local shaping)，根据其法向量和当前形状决定其每个面片的位置和朝向。然后进行全局融合(global blending)，将所有面片粘合在一起（其在局部成形后会破碎），使表面重新相连。融合在最小二乘优化框架下进行，可以高效求解。
该文章是首次运用DGP求解SfG(surface from gradients, 即surface from normal)问题，其优势有三方面：
1.保存尖锐特征：由于法向量仅在局部成形步骤里被强制在面片内，尖锐特征可以沿着面片边界构建。同时，表面平滑度由于全局渲染步骤的最小二乘优化而保存
2.应对梯度信息缺失：可应用缺失法向量信息的样本。缺失55%信息的样本也可成功重建
3.应对规则边界：由于将计算媒介转换到mesh的表面，具有一般形状边界的表面也可有效重建
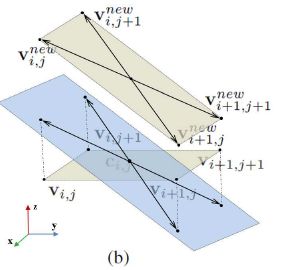
局部成形和全局融合的示意图：

可以看到，整个算法的思路就是：每个像素就是一个面片，一开始M是一个平面，然后根据每个面片的法向量摆正面片的方向，最后把面片垒起来，不断迭代以获得最终结果。

2.论文的范式

首先，对于每个样本(i,j)，为其构建一个四边形面片$f_{i,j}$，面片的边界由四个顶点定义：$v_{i,j},v_{i+1,j},v_{i+1,j+1},v_{i,j+1}$。

2.1 Local Shaping 局部成形

在局部成形步骤，四边形面片$f_{i,j}$的顶点投影到具有法向量$n_{i,j}$的平面，该平面假设穿过当前面片$f_{i,j}$的中心$c_{i,j}$：

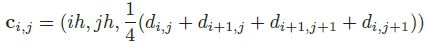
顶点$v_{k,l}$沿z轴在法向量平面的投影(新的z坐标)由下式给出：

其中k的取值为{i,i+1},l的取值为{j,j+1}，
具体来说，假设四个顶点投影后的深度为d，面片中心的深度为c，则：
$$\{\begin{array}{l}{d}_{i,j}=c\\ d_{i+1,j}=c-\frac{n_x\ast h}{n_z}\\ d_{i+1,j+1}=c-\frac{n_x\ast h+n_y\ast h}{n_z}\\ d_{i,j+1}=c-\frac{n_y\ast h}{n_z}\end{array}$$
其中h为设定的每个像素所代表的宽度
因为这个投影公式只是一个近似值，由下式给出也是可以的（论文中没写，但实验过可行，我感觉按论文示意图的话，下式可能更合理？）：
$$\{\begin{array}{l}{d}_{i,j}=c-\frac{n_x\ast (-0.5)\ast h+n_y\ast (-0.5)\ast h}{n_z}\\ d_{i+1,j}=c-\frac{n_x\ast (-0.5+1)\ast h+n_y\ast (-0.5)\ast h}{n_z}\\ d_{i+1,j+1}=c-\frac{n_x\ast (-0.5+1)\ast h+n_y\ast (-0.5+1)\ast h}{n_z}\\ d_{i,j+1}=c-\frac{n_x\ast (-0.5)\ast h+n_y\ast (-0.5+1)\ast h}{n_z}\end{array}$$
Local Shaping示意图：

依笔者愚见，在顶点的下标中$v_{i,j},v_{i+1,j},v_{i+1,j+1},v_{i,j+1}$如果换为$v_{i+1,j},v_{i+1,j+1},v_{i,j+1},v_{i,j}$可能更合理（即i对应x，j对应y，i+1对应x坐标增加）
上面这样的示意图按第二种方式投影后的坐标示意如下：

由四个面片包围的顶点$v_{k,l}$会计算出4个投影坐标，如果我们简单对其求平均获得该顶点的投影坐标，结果会不尽如人意，因此我们需要更加复杂的全局融合。

2.2 Global Blending 全局融合

在全局融合步骤里，我们希望将M变形为这样一个形状：其所有面片以顶点位置所给出的形状与投影后的面片一样。具体来说，假设$z(f_{i,j})$是由面片$f_{i,j}$各顶点深度组成的向量（这里的z应理解为经过global blending后的深度）：

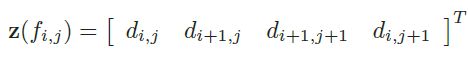
设投影后面片的顶点深度向量为$p(f_{i,j})$，在最优形状M中，向量z和向量p应该表示一个相同形状的面片，这个目标可以表示为最小化下式：

通过最小化上式，可以获得mesh表面M，其表面法向量与目标最接近，然而该约束过强，实际上z和p仅被希望表示相同的形状。因此我们建立新的式子，通过对比它们（投影后的面片和global blending后的面片）以它们中心为参考的的相对向量（relative vector）。这个可以通过减去z和p的均值来实现。即我们定义这样一个矩阵：

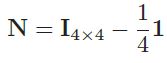
其中$I$是单位矩阵，$1$是一个元素全为1的4x4矩阵
$Nz(f_{i,j})$返回面片$z(f_{i,j})$以其中心为参考的相对向量，示意图如下，观察可知相对向量(4x1)是面片中心指向四个顶点的向量的z值的集合，可以表征面片的形状和朝向。$Np(f_{i,j})$也一样。此时我们要优化的函数为：
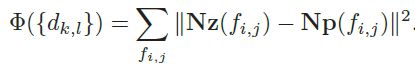如下图所示，当z和p有相同形状和相同朝向时获得最小值。蓝色是当前facet用式(2)投影后的4个顶点构成的新facet，由于每个顶点在4个相邻的facet各自投影后都会获得新的高度值，因此黄色是每个顶点用某种策略(global blending)融合4个分别的投影后形成的顶点所构成的新的facet，我们不希望这两个facet顶点位置完全一样，这样约束太严格，我们希望的是黄色facet和蓝色facet的形状和朝向相同即可，因此2.3节方程组所求的深度x就是黄色facet的顶点深度，方程组的思想是，先局部投影，然后再全局求解，让全部面片的融合深度值整体最优

最后，面片中心的深度值由四个顶点求平均得到

2.3数学方案

将上面的优化问题改写为下式：

我们假设待重建表面有n个顶点，m个面片，其中，A是一个大小为4mxn的稀疏矩阵，x为待求解的global blending后每个顶点的深度，b为投影后面片$pi,j$的各个顶点的相对向量的各个值排列得到的列向量。Ax的结果为global blending后的面片各个顶点的相对向量的各个值排列得到的列向量。因此A在每次迭代中都是一样的，可以提前构造，b需要在每次迭代中更新。

在代码中，我们可以分4个mxn矩阵来构造A，第i个mxn矩阵填充的是论文中N的第i行数据与z($f_{i,j}$)(这里的$f_{i,j}$是global blending后的$f_{i,j}$)相乘的结果，这个矩阵每行会有四个值(N每行那几个), 每行代表一个面片, 这四个值存放列的列索引对应当前行的面片的四个顶点的索引，因此它与x相乘后得到一个所有facet的relative vector的第i个值排列得到的列向量, 与之相对应的b应为N的第i行与p($f_{i,j}$)的所有facet顶点相乘得到的relative vector的第i个值排列得到的列向量

这样一个基础最小二乘问题可以由下式求解：

若把上式记为$Cx=d,C=A^{T}A,d=A^{T}b$
我们可以先对$C$进行Cholesky因式分解（一个实对称正定矩阵$C$可以分解为两个下三角矩阵的乘积$C=L{L}^T$），因此在每次迭代中，我们只需要这样计算x的值：
$Ly=d,L^{T}x=y$

2.4异常处理

当法向量确定的平面与xoy平面接近垂直时，局部成形会变得不稳定（待投影的平面过于垂直），这时做一个异常检测，当$n_{i,j}\ast (0,0,1)\le ϵ$，作者使用$ϵ=0.0871557$，这时表面角度小于5°，这些法向量定义为离群值，这时，将$z(f_{i,j})$的法向量用作$p(f_{i,j})$的法向量，即法向量不变，或者说面片不变形。

在代码中如何更新离群面片的法向量呢，在获得与其对应的global blending后的面片后，由于这个面片被四个顶点所定义，这时的面片已经未必是平面四边形，即四点未必共面，我们利用三点确定一个平面（或由两个向量确定），构建两组平面（两组三点），在其中一组中，求解一个不满秩的方程组得通解：
$V_{2x3}n=0$
但如果碰上使用的计算包不能计算这种方程组(如scipy和numpy就不行)，我们可以转化为特征值的计算，可以证明$V^{T}V$特征值为0对应的特征向量就是上式的通解。

3.代码

代码我放在了GitHub上：看着代码应该可以更好理解这篇文章的思想，Click me

这篇文章的延申工作：
3D Surface Detail Enhancement From a Single Normal Map

Surface Reconstruction From Normals: A Robust DGP-Based Discontinuity Preservation Approach

Surface Reconstruction with Unconnected Normal Maps: An Efficient Mesh-based Approach

最后就以小bunny结束这篇文章吧。