pandas中计算分位数的方法describe，quantile，以及sql中计算分位数的方法percentile_approx,percent_rank() over()

1.pandas中计算分位数的方法describe，quantile

准备一张表

def test():
    df = pd.DataFrame({'a':[1,2,3],'b':[4,5,6],'c':['d','e','f']})
    print(df)

表结构如下：

（1）p分位数原理和计算过程

例：a =[20,10,30]，求这组数的四分之一，二分之一，四分之三分位数，即p=0.25,p=0.5,p=0.75的情况

1.从小到大排序[10,20,30]，长度n = len(a) = 3
2.使用公式求分位数位置，即分位点：pos = 1 + (n-1)*p
pos(0.25) = 1 + (3-1)*0.25 = 1.5 向下取整结果为pos(0.25)_low = 1，分位点小数部分0.5
pos(0.5) = 1+(3-1)*0.5 = 2 向下取整结果为pos(0.5)_low = 2，分位点小数部分0
pos(0.75) = 1 + (3-1)*0.75 = 2.5 向下取整结果为pos(0.75)_low = 2，分位点小数部分0.5
需要注意的是分位点的小数部分，影响着最终分位数的结果
3.求分位数
排序后，a[0] = 10，a[1]=20，a[2] = 30

四分之一：a[pos(0.25)_low -1]  + (a[pos(0.25)_low]-a[pos(0.25)_low -1]) * (pos(0.25)-pos(0.25)_low)  = a[0] + (a[1]-a[0])*(1.5-1) = 15
二分之一：a[pos(0.5)_low -1]  + (a[pos(0.5)_low]-a[pos(0.5)_low -1]) * (pos(0.5)-pos(0.5)_low)  = a[1] + (a[2]-a[1])*(2-2) = 20
四分之三：a[pos(0.75)_low -1]  + (a[pos(0.75)_low]-a[pos(0.75)_low -1]) * (pos(0.75)-pos(0.75)_low)  = a[1] + (a[2]-a[1])*(2.5-2) = 25

p分位数可以用于分组，即将任意个数的数据从小到大进行分组，使得每一组的包含的数据的个数都近似相等，等频分箱

（2）describe

def test():
    df = pd.DataFrame({'a':[1,2,3],'b':[4,5,6],'c':['d','e','f']})
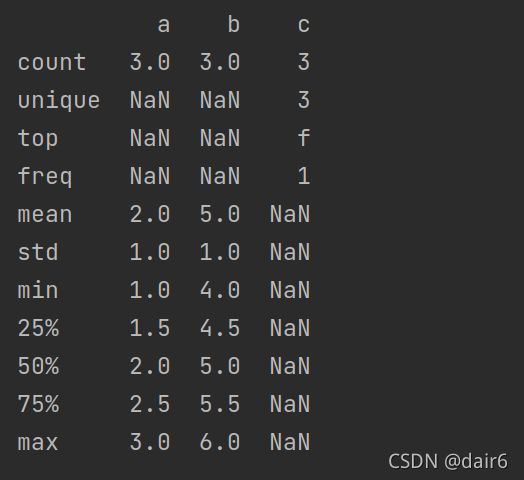
    print(df.describe(include='all'))
    # 需要注意的是，要加上'all'，否则，只会分析a，b数字列
    # 也可以分析单列
    print(df['a'].describe())
    # 也可指定分位数
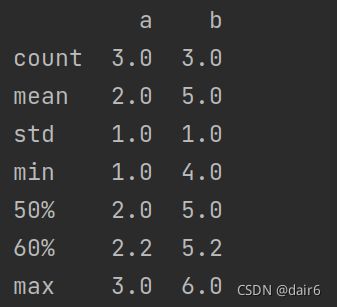
    print(df.describe(percentiles=[0.6]))

结果如下：

含义如下，
count：某一列中非空数据的个数
unique:非数字型的值去重后的个数
top:出现最多次数的痱数字型的值–由上图可知，如果一些值出现次数相同，只会取其中一个作为top
freq:出现最多次数的痱数字型的值出现的次数
mean:平均值
std:标准差
min:最小值
25%:四分之一分位数
50%:二分之一分位数
75%:四分之三分位数
max:最大值

（3）quantile

def test():
    df = pd.DataFrame({'a':[1,2,3],'b':[4,5,6],'c':['d','e','f']})
    print(df['a'].quantile(0.25))

结果为1.5
需要注意的是，如果分为点为两个数之间，比如说这个例子，分位点为1 + (3-1)*0.25 = 1.5，即第一个数a[0]和第二个数a[1]之间，如下图，有5中不同的设置分位点的方式，不同的方式，导致分位点的小数部分不同，因为计算分位数时需要用到分位点小数部分，导致最终分位数也会不同

def test():
    df = pd.DataFrame({'a':[1,2,3],'b':[4,5,6],'c':['d','e','f']})
    print(df['a'].quantile(0.25,interpolation='linear'))     #使用公式1+(n-1)*p得出分位点1.5，分位数为1+(2-1)*0.5=1.5
    print(df['a'].quantile(0.25,interpolation='lower'))      #使用公式1+(n-1)*p得出结果1.5，取1为分位点，即第一个数a[0]，分位数为1+(2-1)*0=1
    print(df['a'].quantile(0.25,interpolation='higher'))   #使用公式1+(n-1)*p得出结果1.5，取2为分位点，即第二个数a[1]，分位数为2+(3-2)*0=2
    print(df['a'].quantile(0.25,interpolation='nearest')) #使用公式1+(n-1)*p得出结果1.5，靠近1，则取1为分位点，靠近2，取2为分位点，1.5在中间，算是靠近1
    print(df['a'].quantile(0.25,interpolation='midpoint')) #使用公式1+(n-1)*p得出结果1.5,取左右平均值，即(1+2)/2作为分位点，这里恰巧和公式得出的结果一样

结果为：

2.sql中percentile_approx,percent_rank() over()

(1)percentile_approx

%spark.sql
 select percentile_approx(order_payment_amt, array(0.25, 0.5, 0.75), 100)  # 默认精度为10000，这里设置为100，精度越小，消耗资源越少，array数组中即为百分位数
 from alg.alg_test_jr_tag_19;

结果为：

(2)percent_rank() over(partiton by…order by…)

     judge_customer as (
         select order_phone_num,
                rfm_score,
                --PARTITION BY ：分组子句，表示分析函数的计算范围，不同的组互不相干；  ORDER BY： 排序子句，表示分组后，组内的排序方式；
                --不需要partition by，因为整个表就相当对于一组
                round(percent_rank() over (order by rfm_score), 2) as percent_cus   --结果为每行的百分比，范围[0,1]
         from put_score
     ),
     ```