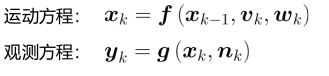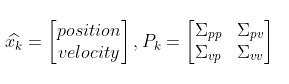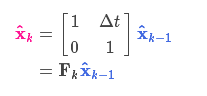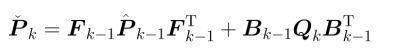基于卡尔曼滤波器的融合IMU与雷达/深蓝多传感器融合第七章作业
1、卡尔曼滤波介绍
参考
详解卡尔曼滤波原理_清风莞尔的博客-CSDN博客_卡尔曼滤波原理
1、运动方程与观测方程
其中
代表位置和速度
Vk代表输入输入,Wk代表噪声
运动方程表示已知k-1时刻的状态和k时刻的输入来预测k时刻的状态(位姿)
当融合imu与雷达信息时,由imu得到预测即运动方程(状态方程),雷达得到观测方程
观测方程表示在k时刻已知状态xk和噪声nk观测到环境中物体yk。在此融合问题中由
2、线形高斯假设重写两个方程
运动方程
k-1时刻机器人状态服从一个高斯分布,我们根据一个变换和输入预测k时刻的状态分布;以下是k-1时刻的均值和协方差矩阵
我们要得到k时刻的状态的高斯分布要求出k时刻的均值与协方差
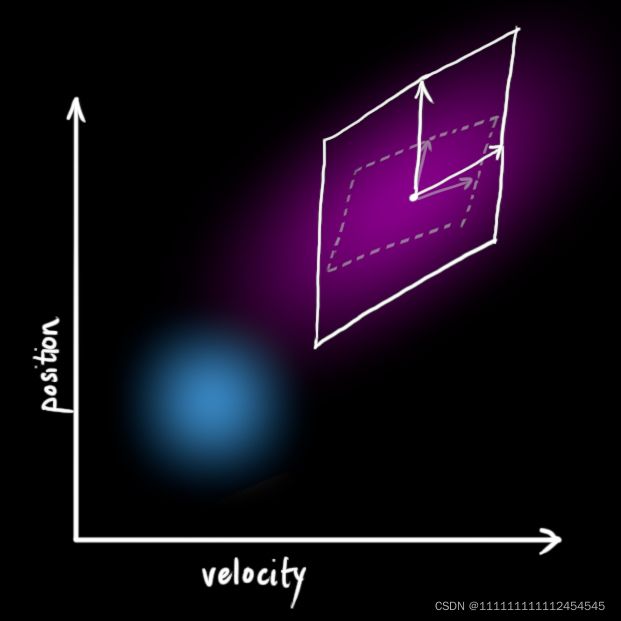
用矩阵Fk来表示预测过程则
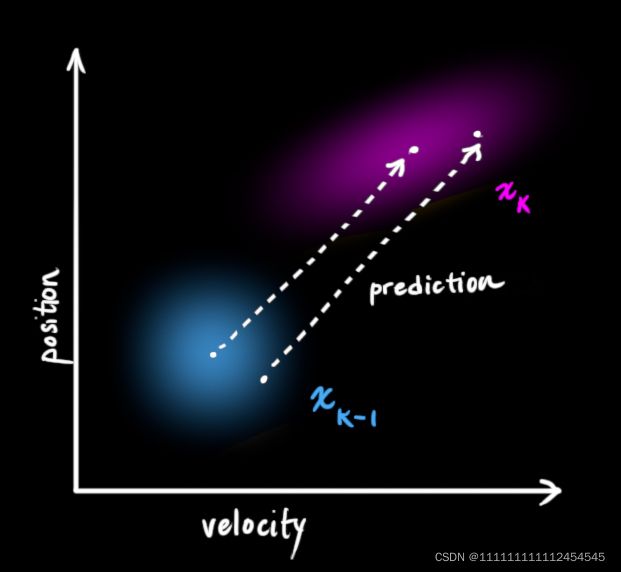
用图形表示为:
协方差矩阵变为:
添加上噪声Q后预测变为:
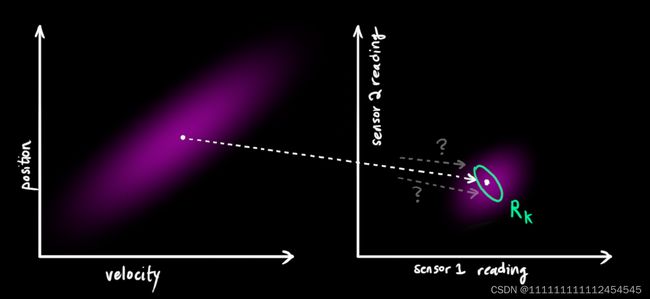
观测方程
k时刻有传感器进(雷达)行了观测,所以我们可以用雷达观测的数据(也服从一个高斯分布)和imu预测的结果结合得到更精确的结果
同样的我们由观测到到数据也会产生由观测计算出来的新的状态。即知道由雷达观测,通过前端(icp,ndt,loam)等方式计算位姿
当传感器有一定的误差时位姿计算变为:
3、卡尔曼滤波融合
高斯分布融合基础
我们现在知道两个状态的高斯分布,一个是imu预测得到的状态分布,一个是雷达观测当前时刻计算出的状态的高斯分布,将两个高斯分布融合得到新的一个状态的高斯分布就是我们要的融合结果
用图形表示如下:
粉色表示预测值绿色表示观测值,中间交集部分即为我们要的滤波后的接近真实值的值。
推导见参考博客
融合IMU与雷达 
该式表示,已知初始时刻状态,和1到k时刻的输入,以及前面时刻的观测,来计算当前状态(位姿即定位任务)和观测(即建图任务)
该式就融合了imu预测(x0,v1:k)和雷达观测(y0:k)从而求出新的状态(位姿进行定位)
均值和协方差矩阵计算方法参照上一部分
再进行整理得到
第一个式子是卡尔曼增益
第二个式子是融合之后的高斯分布的协方差矩阵
第三个式子是融合后的高斯分布的均值
第四个式子是预测状态(运动方程)的高斯分布的均值
第五个式子是预测状态的高斯分布的协方差
状态方程构建
观测方程构建
构建滤波器
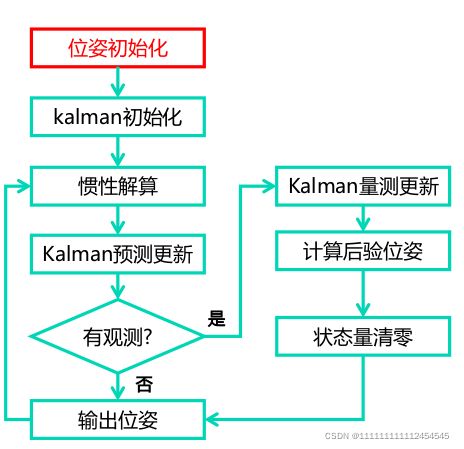
流程
代码详解
1、更新里程计信息
void ErrorStateKalmanFilter::UpdateOdomEstimation(
Eigen::Vector3d &linear_acc_mid, Eigen::Vector3d &angular_vel_mid) {
//
// TODO: this is one possible solution to previous chapter, IMU Navigation,
// assignment
//
// get deltas:
Eigen::Vector3d deltas=Eigen::Vector3d::Zero();
size_t index_curr_=1;
size_t index_prev_=0;
GetAngularDelta(index_curr_, index_prev_, deltas, angular_vel_mid);
// update orientation:
Eigen::Matrix3d R_curr_ =Eigen::Matrix3d::Identity();
Eigen::Matrix3d R_prev_ =Eigen::Matrix3d::Identity();
UpdateOrientation(deltas,R_curr_,R_prev_);
// get velocity delta:
double delta_t_=0;
Eigen::Vector3d velocity_delta_=Eigen::Vector3d::Zero();
GetVelocityDelta(index_curr_,index_prev_,R_curr_,R_prev_,delta_t_,velocity_delta_,linear_acc_mid);
// save mid-value unbiased linear acc for error-state update:
// update position:
UpdatePosition(delta_t_, velocity_delta_);
}这部分是上一章内容
参考
惯性传感器导航解算/多传感器融合6_dushib的博客-CSDN博客
2、求解F和B
void ErrorStateKalmanFilter::SetProcessEquation(const Eigen::Matrix3d &C_nb,
const Eigen::Vector3d &f_b,
const Eigen::Vector3d &w_b) {
// TODO: set process / system equation:
// a. set process equation for delta vel:
F_.setZero();
F_.block<3, 3>(kIndexErrorPos, kIndexErrorVel) = Eigen::Matrix3d::Identity();
F_.block<3, 3>(kIndexErrorVel, kIndexErrorOri) = - C_nb * Sophus::SO3d::hat(f_b).matrix();
F_.block<3, 3>(kIndexErrorVel, kIndexErrorAccel) = -C_nb;
F_.block<3, 3>(kIndexErrorOri, kIndexErrorOri) = - Sophus::SO3d::hat(w_b).matrix();
F_.block<3, 3>(kIndexErrorOri, kIndexErrorGyro) = - Eigen::Matrix3d::Identity();
// b. set process equation for delta ori:
B_.setZero();
B_.block<3, 3>(kIndexErrorVel, kIndexNoiseGyro) = C_nb;
B_.block<3, 3>(kIndexErrorOri, kIndexNoiseGyro) = Eigen::Matrix3d::Identity();
B_.block<3, 3>(kIndexErrorAccel, kIndexNoiseBiasAccel) = Eigen::Matrix3d::Identity();
B_.block<3, 3>(kIndexErrorGyro, kIndexNoiseBiasGyro) = Eigen::Matrix3d::Identity();
}在.h中定义这些变量为private防止被改动
private:
// indices:
static constexpr int kDimState{15};
static constexpr int kIndexErrorPos{0};
static constexpr int kIndexErrorVel{3};
static constexpr int kIndexErrorOri{6};
static constexpr int kIndexErrorAccel{9};
static constexpr int kIndexErrorGyro{12};
static constexpr int kDimProcessNoise{12};
static constexpr int kIndexNoiseAccel{0};
static constexpr int kIndexNoiseGyro{3};
static constexpr int kIndexNoiseBiasAccel{6};
static constexpr int kIndexNoiseBiasGyro{9};
// dimensions:
static constexpr int kDimMeasurementPose{6};
static const int kDimMeasurementPoseNoise{6};F和B初始化定义如下:
F:15*15
B:15*12
using MatrixF=Eigen::Matrix;
using MatrixB=Eigen::Matrix; using用法:
c++中using的用法_YoungYangD的博客-CSDN博客_c++ using
eigen block用法:
Eigen子矩阵操作(block)_不二青衣的博客-CSDN博客_eigen.block
此函数求解F和B为写出运动方程作准备
注释:
此处每一个0都代表一个3*3的0矩阵,所以先将F声明成一个15*15的零矩阵
3、 kalman预测
void ErrorStateKalmanFilter::UpdateErrorEstimation(
const double &T, const Eigen::Vector3d &linear_acc_mid,
const Eigen::Vector3d &angular_vel_mid) {
static MatrixF F_1st;
static MatrixF F;
// TODO: update process equation:
UpdateProcessEquation(linear_acc_mid,angular_vel_mid);
// TODO: get discretized process equations:
F_1st=F_*T;
F=MatrixF::Identity()+F_1st;
MatrixB B=MatrixB::Zero();
B.block<3, 3>(kIndexErrorVel, kIndexNoiseGyro) = B_.block<3, 3>(kIndexErrorVel, kIndexNoiseGyro) * T;
B.block<3, 3>(kIndexErrorOri, kIndexNoiseGyro) = B_.block<3, 3>(kIndexErrorOri, kIndexNoiseGyro) *T;
B.block<3, 3>(kIndexErrorAccel, kIndexNoiseBiasAccel) = B_.block<3, 3>(kIndexErrorAccel, kIndexNoiseBiasAccel)* sqrt(T);
B.block<3, 3>(kIndexErrorGyro, kIndexNoiseBiasGyro) = B_.block<3, 3>(kIndexErrorGyro, kIndexNoiseBiasGyro)* sqrt(T);
// TODO: perform Kalman prediction
X_=F*X_;
P_=F*P_*F.transpose()+B*Q_*B.transpose();
}离散化
static MatrixF F_1st;
static MatrixF F;
// TODO: update process equation:
UpdateProcessEquation(linear_acc_mid,angular_vel_mid);
// TODO: get discretized process equations:
F_1st=F_*T;
F=MatrixF::Identity()+F_1st;
MatrixB B=MatrixB::Zero();
B.block<3, 3>(kIndexErrorVel, kIndexNoiseGyro) = B_.block<3, 3>(kIndexErrorVel, kIndexNoiseGyro) * T;
B.block<3, 3>(kIndexErrorOri, kIndexNoiseGyro) = B_.block<3, 3>(kIndexErrorOri, kIndexNoiseGyro) *T;
B.block<3, 3>(kIndexErrorAccel, kIndexNoiseBiasAccel) = B_.block<3, 3>(kIndexErrorAccel, kIndexNoiseBiasAccel)* sqrt(T);
B.block<3, 3>(kIndexErrorGyro, kIndexNoiseBiasGyro) = B_.block<3, 3>(kIndexErrorGyro, kIndexNoiseBiasGyro)* sqrt(T);
// TODO: perform Kalman prediction
X_=F*X_;
P_=F*P_*F.transpose()+B*Q_*B.transpose();
}运动方程
X_=F*X_;协方差矩阵
P_=F*P_*F.transpose()+B*Q_*B.transpose();4、观测更新
void ErrorStateKalmanFilter::CorrectErrorEstimationPose( // 计算 Y ,G ,K
const Eigen::Matrix4d &T_nb, Eigen::VectorXd &Y, Eigen::MatrixXd &G,
Eigen::MatrixXd &K) {
//
// TODO: set measurement: 计算观测 delta pos 、 delta ori
//
Eigen::Vector3d dp = pose_.block<3, 1>(0, 3) - T_nb.block<3, 1>(0, 3);
Eigen::Matrix3d dR = T_nb.block<3, 3>(0, 0).transpose() * pose_.block<3, 3>(0, 0) ;
// TODO: set measurement equation:
Eigen::Vector3d dtheta = Sophus::SO3d::vee(dR - Eigen::Matrix3d::Identity() );
YPose_.block<3, 1>(0, 0) = dp; // delta position
YPose_.block<3, 1>(3, 0) = dtheta; // 失准角
Y = YPose_;
// set measurement G
GPose_.setZero();
GPose_.block<3, 3>(0, kIndexErrorPos) = Eigen::Matrix3d::Identity();
GPose_.block<3 ,3>(3, kIndexErrorOri) = Eigen::Matrix3d::Identity();
G = GPose_;
// set measurement C
CPose_.setZero();
CPose_.block<3, 3>(0,kIndexNoiseAccel) = Eigen::Matrix3d::Identity();
CPose_.block<3, 3>(3,kIndexNoiseGyro) = Eigen::Matrix3d::Identity();
Eigen::MatrixXd C = CPose_;
// TODO: set Kalman gain:
Eigen::MatrixXd R = RPose_; // 观测噪声
K = P_ * G.transpose() * ( G * P_ * G.transpose( ) + C * RPose_* C.transpose() ).inverse() ;
}
void ErrorStateKalmanFilter::CorrectErrorEstimation(
const MeasurementType &measurement_type, const Measurement &measurement) {
//
// TODO: understand ESKF correct workflow
//
Eigen::VectorXd Y;
Eigen::MatrixXd G, K;
switch (measurement_type) {
case MeasurementType::POSE:
CorrectErrorEstimationPose(measurement.T_nb, Y, G, K);
break;
default:
break;
}
// TODO: perform Kalman correct:
P_ = (MatrixP::Identity() - K*G) * P_; // fix this
X_ = X_ + K * (Y - G*X_); // fix this
}详解
Eigen::Vector3d dp = pose_.block<3, 1>(0, 3) - T_nb.block<3, 1>(0, 3);Eigen::Matrix3d dR = T_nb.block<3, 3>(0, 0).transpose() * pose_.block<3, 3>(0, 0) ;Eigen::Vector3d dtheta = Sophus::SO3d::vee(dR - Eigen::Matrix3d::Identity() );YPose_.block<3, 1>(0, 0) = dp; // delta position
YPose_.block<3, 1>(3, 0) = dtheta; // 失准角 GPose_.setZero();
GPose_.block<3, 3>(0, kIndexErrorPos) = Eigen::Matrix3d::Identity();
GPose_.block<3 ,3>(3, kIndexErrorOri) = Eigen::Matrix3d::Identity();
G = GPose_; CPose_.setZero();
CPose_.block<3, 3>(0,kIndexNoiseAccel) = Eigen::Matrix3d::Identity();
CPose_.block<3, 3>(3,kIndexNoiseGyro) = Eigen::Matrix3d::Identity();
Eigen::MatrixXd C = CPose_; K = P_ * G.transpose() * ( G * P_ * G.transpose( ) + C * RPose_* C.transpose() ).inverse() ; P_ = (MatrixP::Identity() - K*G) * P_; // fix this
X_ = X_ + K * (Y - G*X_); // fix this5、 后验位姿
void ErrorStateKalmanFilter::EliminateError(void) {
// 误差状态量 X_ : 15*1
// TODO: correct state estimation using the state of ESKF
//
// a. position:
// do it!
pose_.block<3, 1>(0, 3) -= X_.block<3, 1>(kIndexErrorPos, 0 ); // 减去error
// b. velocity:
// do it!
vel_ -= X_.block<3,1>(kIndexErrorVel, 0 );
// c. orientation:
// do it!
Eigen::Matrix3d dtheta_cross = Sophus::SO3d::hat(X_.block<3,1>(kIndexErrorOri, 0)); // 失准角的反对称矩阵
pose_.block<3, 3>(0, 0) = pose_.block<3, 3>(0, 0) * (Eigen::Matrix3d::Identity() - dtheta_cross);
Eigen::Quaterniond q_tmp(pose_.block<3, 3>(0, 0) );
q_tmp.normalize(); // 为了保证旋转矩阵是正定的
pose_.block<3, 3>(0, 0) = q_tmp.toRotationMatrix();
// d. gyro bias:
if (IsCovStable(kIndexErrorGyro)) {
gyro_bias_ -= X_.block<3, 1>(kIndexErrorGyro, 0); // 判断gyro_bias_error是否可观
}
// e. accel bias:
if (IsCovStable(kIndexErrorAccel)) {
accl_bias_ -= X_.block<3, 1>(kIndexErrorAccel, 0); // 判断accel_bias_error是否可观
}
}6、结果
参考
详解卡尔曼滤波原理_清风莞尔的博客-CSDN博客_卡尔曼滤波原理
c++中using的用法_YoungYangD的博客-CSDN博客_c++ using
Eigen子矩阵操作(block)_不二青衣的博客-CSDN博客_eigen.block
惯性传感器导航解算/多传感器融合6_dushib的博客-CSDN博客
深蓝学院多传感器融合课程第七章课件
深蓝学院-多传感器融合定位-第7章作业_Weiheng-Summer的博客-CSDN博客