深度学习课程笔记-第二周
title: 深度学习课程笔记-第二周
date: 2022-11-20 21:58:31
对于有m个训练集的样本,并不需要for循环遍历整个样本。
【2.1 二分分类】
在神经网络的计算中,通常有一个正向的传播和一个反向的传播。神经网络的计算过程可以分为 前向传播和反向传播 (用logistics回归来阐述)
(什么是logistics回归:
Logistics回归是统计学习中的经典分类方法,是一种广义的线性回归模型。它经常被使用于二分类问题的解决上,具有不错的效果。
Logistics回归是在线性回归的基础上,加入了sigmoid函数,使函数的取值分布在[ 0 , 1 ]之间,从而使模型具有分类的效果。)
logistics回归是一个用于二分分类的算法。
引例:二分分类问题
假设有一张图片作为输出,想输出识别此图的标签:如果是猫,输出1;如果不是,则输出0。
注:一张图片,在计算机中是如何表示的?
计算机保存一张图片,要保存三个独立矩阵,分别对应图片中的红绿蓝三个颜色通道。
eg:输出图片是64×64像素的,就有三个64×64的矩阵,分别对应图片中红绿蓝三种像素的亮度。

eg:用三个5×4的小矩阵。要把这些像素亮度值放进一个特征向量中,就要把这些像素值都提出来放入一个特征向量x。定义一个特征向量X以表示这张图片,我们把所有的像素值都取出来(按列叠放),例如255、231……把所有的红色像素列出来,紧接着是255、134、202…(绿色的),255、134、93……(蓝色的),把图片中所有红绿蓝像素强度值都列出来。若图片是64×64的,那么向量x的总维度就是 n=nx=64×64×3=12288(三个矩阵的元素数量)。
如图:

那么回到正题,在二分分类问题中,目标是训练出一个分类器 ——它以图片的特征向量x作为输入,预测输出的结果标签y(1 or 0),即预测图片中是否有猫。
一些符号约定:
-
**(x,y)**表示一个单独的样本。x是n~x~维的特征向量,标签y=1or 0。 -
训练集由m个训练样本构成,**m**表示训练样本的个数。有时为了强调:m=m~train~(训练样本个数), m=m~test~(测试集样本个数) -
(x1,y1)表示样本1 ,(x2,y2) 表示样本2……(xm,ym)表示样本m。m={(x1,y1),(x2,y2)……(xm,ym)}
-
可以用更紧凑的方式表示训练集,定义一个矩阵,用大写X表示,如图:
 X是一个(n~x~, m)维的矩阵
X是一个(n~x~, m)维的矩阵
-
同样,可以对y标签简化,如图:
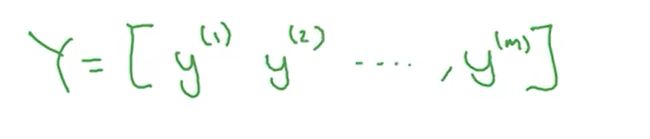 Y是一个(1, m)的矩阵
Y是一个(1, m)的矩阵
【2.2 logistics回归】
这是一个用在监督学习问题中的一种学习算法, 二元分类问题
eg:已知的输入特征向量x是一张猫图, y ^ \widehat{y} y =P(y=1| x)(预测值 y ^ \widehat{y} y 为对y值的预测),我们希望 y ^ \widehat{y} y 告诉我们这是一张猫图的概率(即特征向量x满足条件时y=1的概率)
已知输入x(nx维向量),logistics回归的参数w(nx维向量), 实数b。 y ^ \widehat{y} y 是概率,单纯的线性回归无法保证其值介于[0,1],所以引用sigmoid function(非线性的S型函数)(
也称为sigmoid激活函数,主要作用就是将线性函数转换成非线性函数)保证 y ^ \widehat{y} y 的值在[0,1]之间。即 y ^ \widehat{y} y = σ \sigma σ(wTx + b)
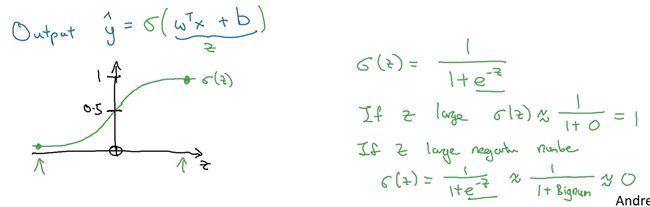 (logistics回归模型如上图)
(logistics回归模型如上图)
【2.3 logistic回归损失函数】
一些符号约定: y ^ \widehat{y} y = σ \sigma σ(wTx(i) + b), σ \sigma σ(z(i))=1/1+e-z(i), i表示x,y和z与第i个训练样本有关。
为了训练参数w和b,我们需要定义一个cost function(成本函数)来判断怎样的参数才是合适的。
cost function是在当前训练集下的,而loss function(损失函数)是指针对某个样本的。cost function 是loss function的平均。
loss function(损失函数):(适用于单个训练样本。 越小越好)L( y ^ \widehat{y} y ,y) = -(ylog y ^ \widehat{y} y +(1-ylog y ^ \widehat{y} y ))
cost function(成本函数):(衡量 在全体训练样本上的表现,为所有训练样本的损失函数和,与w,b有关。 越小越好)
【2.4 梯度下降法】
目的:用来训练或学习 训练集上的参数w和b。
成本函数J是一个凸函数,利用J来逐步迭代实现(w,b)的变化

如图,成本函数J是一个凸函数,只有一个最优解。(这就是为什么logistics回归使用这个特定成本函数的重要原因之一)。
通过多次的迭代(上图中的红点表示一次迭代)来得到一个全局最优解。

梯度下降法的操作:(重复执行以下操作)
-
w:=w - α \alpha α ∂J(w,b)/∂w(:=表示更新w的值, α \alpha α表示学习率,学习率可以控制每一次迭代、更新或者梯度下降法中的步长。可以用dw代表J的导数,即:w:=w - α \alpha α ∂w)
-
b:=b - α \alpha α ∂b
【2.5 导数】
略……
【2.6更多导数的例子】
略……
【2.7 计算图】
一个神经网络的计算都是按照前向或反向传播来实现的。首先计算出神经网络的输出,然后计算反向输出(计算出对应的梯度或导数)
eg:中logistics回归中,计算J(a,b,c)=3(a+bc)
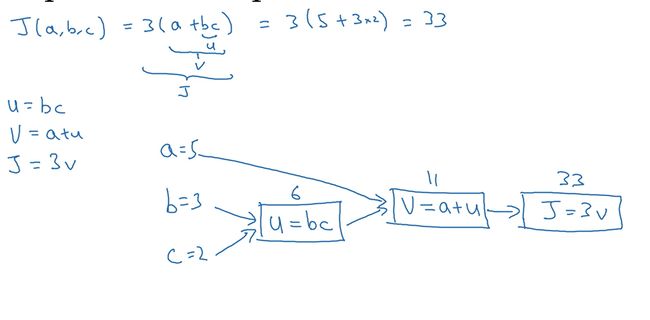
在logistics回归中,J是想要最小化的成本函数。
流程图:从左到右的计算,上图蓝色箭头。
【2.8 计算图的导数计算】

(一些符号约定:我们用dv来代表dJ/dv, da来代表dJ/da,以此类推。)
从右到左(红色箭头)
-
dv: dJ/dv; 这是一步反向传播
-
da: dJ/da=dJ/dv * dv/da; 这是另一步反向传播
-
du : dJ/du= dJ/dv * dv/du ; 这是另一步反向传播
-
db: dJ/db=dJ/du * du/db --> dJ/db= dJ/dv * dv/du * du/db; 这是另一步反向传播
-
dc: dJ/dc=dJ/du * du/dc --> dJ/dc=dJ/dv * dv/du * du/dc; 这是另一步反向传播
【2.9 logistics回归中的梯度下降法 】
通过计算偏导数来实现logistics回归中的梯度下降法。
eg:在考虑单个样本的情况下该样本的损失函数如下:
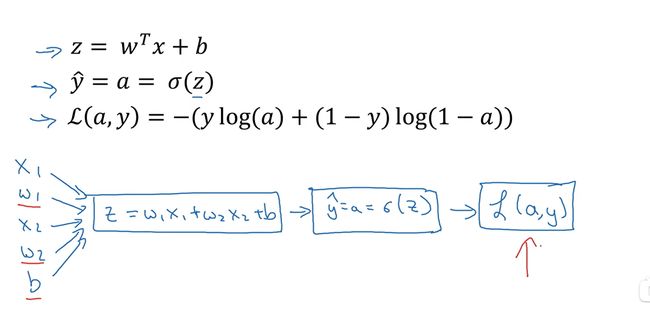
注: y ^ \widehat{y} y =a= σ \sigma σ(z)
a是logistics回归的输出,y是样本的基本真值标签值。
假设样本只有两个特征x1和x2,为了计算z,我们需要输入参数w1,w2和b。
则 z=w1x1+w2x2+b ----> y ^ \widehat{y} y =∂(z) ----> L(a, y)。(向前传播)
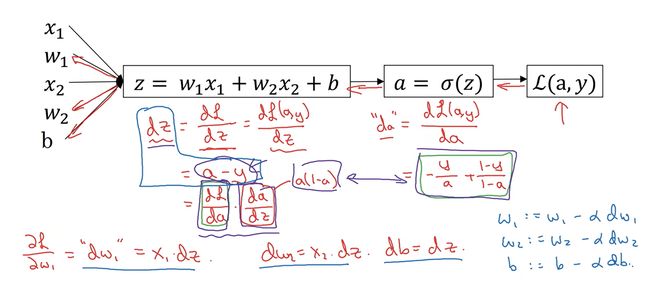
反向传播:
- da=dL(a,y)/da;
- dz=dL/dz=dL(a, y)/dz;
- dw1=dL/dw1, dw2=dL/dw2;
- db=dz;
- 最后再更新w和b的值: w1 := w1- α \alpha αdw1, w2 := w2- α \alpha αdw2, b := b- α \alpha αdb;
这就是单个训练样本样例。
【2.10 m个样本的梯度下降】
注意:a(i)= y ^ \widehat{y} y (i)= σ \sigma σ(z(i))= σ \sigma σ(wTx(i)+b )。 (a(i)是训练样本的预测值。)
- 首先初始化J=0,dw1=0, dw2=0, db=0;
- 然后使用for循环从1到m(假设有两个输入特征w1,w2。如果有更多则继续dw1,dw2,……),如图:
 * 循环结束后:J /= m; dw~1~ /= m; dw~2~ /= m; * 最后更新: w~1~ := w~1~-$\alpha$dw~1~, w~2~ := w~2~-$\alpha$dw~2~, b := b-$\alpha$db;
* 循环结束后:J /= m; dw~1~ /= m; dw~2~ /= m; * 最后更新: w~1~ := w~1~-$\alpha$dw~1~, w~2~ := w~2~-$\alpha$dw~2~, b := b-$\alpha$db;
以上计算的两个缺点:使用了两个for循环(红色部分),一个用来遍历整个训练集m,另一个用来遍历所有的输入特征(w1和w2,如果有更多,则一直遍历到dwn)。 在应用深度学习算法时,显示的使用for循环会使算法很低效,在深度学习领域会有越来越大的数据集,我们会使用一门 向量化技术(Vectorization)来摆脱显式for循环。
【2.11 向量化】
什么是向量化?,在深度学习领域中应用向量化可以减少等待结果的时间。
例如:在logistics回归中,我们需要计算z=wTx+b(w是列向量,x也是列向量)
如图:
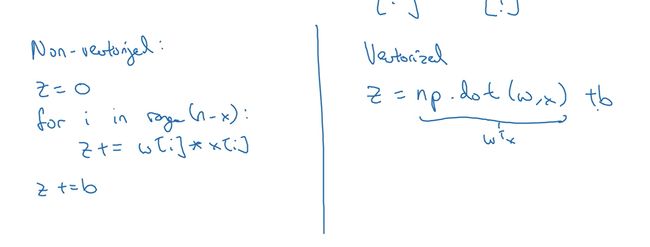 在左边是非向量化的实现,右边是向量化的实现(在python代码中:z=np.dot(w, x) + b)。
在左边是非向量化的实现,右边是向量化的实现(在python代码中:z=np.dot(w, x) + b)。
【2.12 向量化的更多例子】
经验法则:当你在编写新的网络时或只是做回归时,一定要尽量避免for循环,能不用就不用。
-
向量乘法的向量化:u=Av;(u,v是向量,A是矩阵)------> u=np.dot(A, v)
-
指数化的向量化:

将向量v指数化到向量u:u=np.exp(v);
一些补充:
- np.log()会逐个元素计算log
- np.Abs()会计算绝对值
- np.maximun()会计算所有元素的最大值
eg:
 通过对上图进行向量化,得到下图:
通过对上图进行向量化,得到下图:  为了去掉绿色的for循环:
为了去掉绿色的for循环:
我们将dw初始化为一个向量,即dw=np.zeros((nx,1)), 即dw是一个nx × 1维的向量。
【2.13向量化logistics回归】
目的:通过在logistics回归上实现向量化来同时处理整个训练集,来实现梯度下降法的一次迭代。
上图是对m个样本的预测(需要做m次),这是未使用向量化的。
下面是使用向量化的:
-
为了计算z,我们构建一个1 × m的矩阵Z= [z(1),z(2),··········,z(m)]=wTX + [b,b,……b]
其中X是n x×m矩阵,w T是一个行向量


**观察Z=wTX + [b,b,……b]计算结果,第一个元素恰好是z(1),第二个元素恰好是z(2),…… **
为了实现wTX + [b,b,……b],在numpy在使用 Z=np.dot(w.T, x)+ b 实现。其中b是一个实数,但当b加上一个向量时,python会把b自动扩展成一个1×m的行向量(在python在,这个叫做广播(broadcasting))。
- 同理,将[a(1),a(2),……a (m)]横向堆叠起来构成A,即A=[a(1),a(2),……a (m)] = σ \sigma σ(Z)。
以上就实现了对整个训练集正向传播的向量化并且高效计算激活函数。
【2.14 向量化logistics回归的梯度输出】
目的:如何向量化计算m个训练数据的梯度(同时计算)。
dw(1)=a(1)-y(1), dw(2)=a(2)-y(2), ……
我们定义dZ=[dw(1),dw(2),……dw(m)], A=[a(1),a(2),……a (m)], Y=[y(1),y(2),……,y(m) ]
- dZ=A-Y = [a(1)-y(1),a(2)-y(2),……]
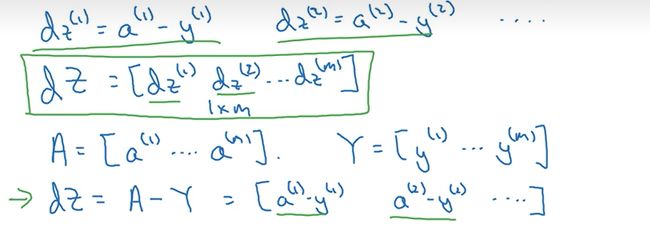
通过观察我们知道dZ的第一项刚好对应dz(1),第二项对应dz(2)……,这就完成了对dZ的初始化

对db和dw进行向量化:

总结:

左边是非向量化的,右边是向量化的。
虽然我们尽量不用显示for循环,但如果需要多次迭代进行梯度下降,那么仍然需要for循环
【2.15 python中的广播】
在python广播中的一些通用规则:
- 如果有一个(m,n)(代表m×n的矩阵)“±×÷” 一个(1,n),那么python会把(1,n)复制m次变成(m,n)
然后在进行 “±×÷”
-
如果有一个(1,n)“±×÷” 一个(m,n),那么python会把(1,n)复制m次变成(m,n)然后在进行
“±×÷”
-
如果有一个(m,1) “±×÷” 一个 R,那么python会把R复制m次变成(m,1)然后在进行
“±×÷”
-
如果有一个(1,n)“±×÷” 一个 R,那么python会把R复制m次变成(1,n)然后在进行
“±×÷”
详情可以参考Numpy手册。
【2.16 关于python_numpy 的向量说明】

不要使用秩为1的数组,尽量使用m×1,1×n,m×n的数组。
如果得到了秩为1的数组,可以通过reshape来转换成,比如5×1的数字: a=a.reshape((5,1))。
如果不确定向量的维数,可以使用arrest来确保这是一个m×1或1×n或m×n的向量。eg:assert(a.reshape==(5,1))。
【2.17 略……】
【2.18 logistics 损失函数的解释】
略……
