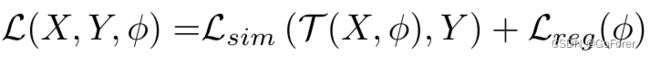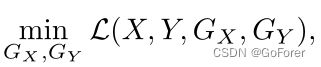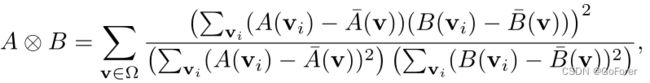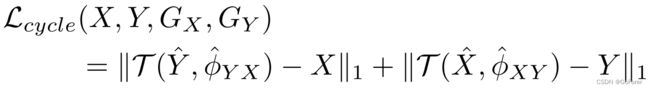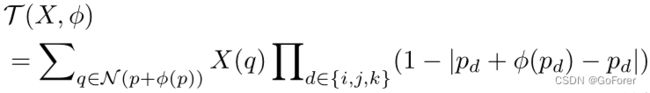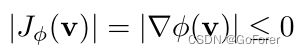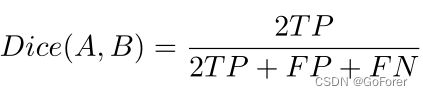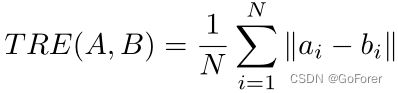论文笔记：CycleMorph: Cycle Consistent UnsupervisedDeformable Image Registration

CycleMorph: Cycle Consistent Unsupervised Deformable Image Registration

针对本篇论文个人总结：

文章最重要的点在于施加循环一致性，模型有两个网络，移动图像与固定图像互相配准过程中施加约束优化网络提高配准精度，仔细看图2。

摘要

现有的深度学习方法在利用配准向量场变形过程中保持原始拓扑方面仍然存在局限性。为了解决这个问题，文章在这里提出了一种循环一致的可变形图像配准。

循环一致性通过提供隐式正则化以在变形期间保持拓扑来增强图像配准性能。所提出的方法非常灵活，可以应用于各种应用的2D和3D配准问题，并且可以容易地扩展到多尺度实现，以处理大体积配准中的内存问题。在来自医学和非医学应用的各种数据集上的实验结果表明，所提出的方法在几秒内在不同的图像对上提供了有效和准确的配准。对变形场的定性和定量评估也验证了所提出方法的循环一致性的有效性。

一、 引言

尽管已经研究了传统的图像配准方法，以使用变分框架解决这一问题，该框架解决了要以相似外观对齐的每个图像对的优化问题，但这些方法通常存在计算量大和配准时间长的问题。

最近，与传统的图像配准方法相比，深度学习方法已经证明了性能的提高。给定源图像和目标图像，深度神经网络被训练以生成与输入图像对相对应的变形场，从而实现显著的快速配准。如今，这些方法已经演变为无监督学习方法，不需要地面真实变形场[15]–[18]。然而，现有的图像配准方法没有明确地执行保证拓扑保持的标准，这通常会导致不准确的配准和结构信息的丢失。

为了克服配准场的潜在退化问题，这里我们提出了一种新的可变形图像配准方法—CycleMorph，该方法使用循环一致性迫使变形图像返回原始图像。与现有方法相比，现有方法对从额外的逆网络生成的变形向量场强制执行逆一致性，这项工作的最重要贡献之一是通过简单地在图像上施加循环一致性来证明拓扑保持。

更具体地说，我们训练了两个卷积神经网络（CNN）Gx和Gy，它们分别生成正向和反向变形向量场。当通过Gx的变形场将运动源图像变形为另一个固定图像时，通过将循环一致性应用于反转图像和原始图像，可以使用Gy的变形场将变形图像反转为原始图像。结果表明，这种具有循环约束的逆路径是在变形过程中提供高性能拓扑保持和较少折叠问题的直接方式。

这项工作的另一个重要创新是扩展到多尺度实现，以处理大体积图像配准。具体而言，由于GPU内存限制，可能无法使用整个3D体积进行图像配准训练。为了解决这一问题，我们提出了一种使用大变形的子采样体积进行粗略3D配准，然后进行局部变形估计以提高配准精度。

为了验证所提出方法的性能，文章将算法应用于不同领域的各种应用，这些领域具有不同的内存需求，包括2D人脸配准、3D脑部MR配准和用于肝癌评估的多相3D腹部对比增强CT（CECT）体积配准。实验结果的定性和定量评估证明了所提出方法的鲁棒性，并证实了循环一致性对拓扑保持的有效性。

论文组织如下。第二节审查相关工作。第三节描述了我们的理论和提出的方法。第四节介绍了面部表情图像、MRI和CT数据集配准的实验结果和讨论，在第六节中得出结论。

二、相关工作

A. Diffeomorphic Image Registration

在经典的变分图像配准方法中，能量函数通常由两项组成：

很多配准的文章中都是基于上式

其中X和Y分别表示运动图像和固定图像；φ表示位移向量场，T是使用变形向量场φ将X扭曲到Y的变换函数。在上式中，第一项是评估变形图像和参考图像之间的形状差异的相似性函数，而第二项是使变形场平滑的正则化函数。

特别是，微分同胚图像(diffeomorphic image)配准方法对向量场φ施加了约束，使得生成的可变形映射变为可微。微分变形确保了两个图像体积之间的某些理想性质，如连续、可微和保持拓扑。这些算法扩展到大变形的流行示例是大变形微分度量匹配（LDDMM）、和对称图像归一化方法（SyN）。

但是这些算法通常在计算上很昂贵，这阻碍了其在临床工作流程中的常规使用。

B. Deep-learning-based Image Registration

基于学习的配准算法是归纳的，一旦训练了神经网络，它就可以立即预测新数据的变形矢量场。因此，它非常适合临床环境。根据网络的训练方式，这些方法可分为两类：监督学习方法和无监督学习方法。在下文中，文章将提供更多详细信息。

1） 监督学习方法：在监督学习方法中，需要变形向量场的基本真值(ground-truth)，通常由经典配准方法生成。Yang等人提出了一种用于变形场逐片预测的编码器-解码器网络，以及一种用于改进变形预测的校正网络。Cao等人开发了一种非刚性多式联运图像配准网络，用于估计两个模态图像的配准场。然而，由于这些方法的配准性能取决于地面真相(ground-truth)的质量，因此这些工作通常需要高质量的地面真相变形场和复杂的预处理，这两者在实践中通常很难获得。

2） 无监督学习方法：为了克服有监督学习方法的局限性，最近开发了无监督学习法，通过最小化变形图像和固定目标图像之间的损失来学习图像配准。Kreb等人通过最小化两个图像分布之间的KL偏差，提出了变形的低维随机参数化的无监督学习模型。Balakrishnan等人提出了一种使用具有空间变换层（STL）的CNN的成对3D医学图像配准算法，这些参数通过归一化互相关函数学习。对于大体积图像配准，V os等人提出了仿射和非刚性图像配准框架，Lei等人通过全局和局部配准网络提出了一种称为MS DIRNet的多尺度无监督学习方法。

然而，这些方法通常不会对一致性施加约束，因此它们会导致映射退化导致折叠问题。尽管Dalca等人引入了一个不同的同胚积分层来解决这个问题，但该约束也应应用于推理阶段，这会增加复杂性。

C. 一致性的图像配准(Consistent Image Registration）

虽然已经提出了经典的微分同胚可变形配准算法来确保一对一的对应性，但变形通常用有限数量的参数离散表示，因此可能存在一些小的违规。因此，估计变形F:X → Y不等于R:Y → X的估计变形的倒数。 在一致性图像配准方法中，通过施加额外的逆一致性来缓解该问题：

特别地，正映射和逆映射 F 和 R 仅通过相应的变形场和来定义，因此相应的逆一致性通常作为正则化项被强制应用于变形向量场。

最近，Zhang提出了一种反向一致性强制深度学习模型，该模型同时训练正向和反向神经网络。正向网络估计可以将源映射到目标的变形场，而反向网络在变形场的反向一致性条件下生成反向流。另一方面，Mahapatra等人通过利用变形图像上的循环一致性提出了基于GAN的图像配准方法。然而，该方法应该具有用于网络训练的完美地标对齐图像对。

三、 理论

图2.用于可变形图像配准的所提出的循环一致深度学习模型CycleMorph的总体框架。两个配准网络（GX、GY）用于通过切换其顺序获取输入。每个网络取两个体积（X，Y），并用三个通道计算位移矢量场。短虚线和长虚线分别表示运动图像和固定图像。空间变换函数根据向量场使运动图像变形以匹配固定图像的形状。这些变换后的图像（X，Y）被带到网络，然后是变换函数，以确保变形图像可以返回到原始状态。

所提出的CycleMmorph的整体学习框架如图2所示。具体而言，对于不同形状或对比度的移动源和固定目标图像X和Y，我们将两个配准网络定义为  和，其中（）表示从X到Y（分别为Y到X）的变形场。我们在网络中使用空间变换层T通过估计的变形场来扭曲运动图像，从而训练配准网络以最小化变形图像和固定图像之间的不相似度。因此，当一对图像被提供给配准网络时，运动图像被变形以与固定图像对齐。

特别地，为了保证变形图像和固定图像之间的拓扑保持，我们在原始运动图像与其重新变形图像之间使用循环一致性约束。也就是说，通过切换它们的顺序以在图像的像素级上施加循环一致性，将两个变形图像再次作为网络的输入。该约束允许网络通过确保变形图像的形状连续返回到原始形状来提供不同的变形。

A. 损失函数(Loss Function)

文章通过解决以下优化问题来训练所提出的循环一致性学习模型：

其中 

其中、和分别是配准损失、循环损失和同一性损失，α和β是超参数。如图3所示，我们的方法以无监督的方式训练，没有地面真实变形场。各损失函数的更详细描述如下。

1） 配准损失(Regist Loss)：配准损失函数基于具有相似性和平滑性惩罚项的传统变分图像配准的能量函数。我们使用相似性函数的局部互相关来降低对比度变化的敏感性，并使用正则化函数的L2损失。因此，我们的配准损失函数可以写成

 其中λ是超参数，是GX的变形向量场，输入X和Y，以及⊗ 表示局部互相关，其通过以下公式计算：

 Ω 表示整个3D体积，而和分别表示体积A(v)和B(v)的局部平均值。这里，在××像素上迭代（或二维配准情况下的×），在我们的研究中＝9。

图3.方法中的损失函数结构图。配准损失函数Regist Loss计算变形图像和固定图像的形状差异。循环损失函数Cycle Loss允许位移场保持运动图像和变形图像之间的拓扑。同一性损失函数Idnentity Loss使网络能够稳定地训练以生成位移矢量场。

2） 循环损失(Cycle Loss)：为了在变形过程中保持拓扑，文章在图像的像素级上设计了循环一致性，如图3所示。具体而言，首先将图像变形为图像，然后通过另一个网络再次配准变形的图像，以在所提出的框架中生成图像。然后，在重新变形的图像与其原始图像之间应用循环一致性，以施加。类似地，图像应通过两个网络连续变形以生成图像，并且循环一致性允许施加。

在这里，文章的配准框架的周期损失的一个重要部分是网络接收两个输入：移动图像和固定图像。因此，循环一致性的正确实现应作为循环一致性条件的向量形式给出：

其中

 因此，循环损耗通过以下公式计算：

 其中表示范式

 3） 同一性损失(Identity Loss)：当通过位移矢量场对图像进行变形时，图像的静止区域不应被改变为固定点。为了考虑这一点并提高配准精度，如图3所示，文章设计了同一性约束，即当相同的图像用作运动图像和固定图像时，输入图像不应变形。我们按照以下方式实施同一性损失：

其中⊗ 表示局部互相关。由于最小化互相关损失的负值允许变形图像和固定图像之间的相似性最大化，因此可以通过不执行变形（或微不足道的身份变形）来实现相同输入的最大化。因此，这种同一性损失防止了不必要的变形，增加了静止区域中变形矢量场估计的稳定性。

B. 空间变换层(Spitial Transformation Layer)

为了利用来自网络的位移向量场φ使运动图像X变形，我们将空间变换层添加到网络中。具体而言，对于实验中的3D图像配准，文章采用了具有三线性插值的3D变换函数，其可以定义为：

其中表示像素索引，表示周围的8像素立方邻域，是3D图像空间中的三个方向。类似地，在2D图像配准的情况下，通过在空间变换层中应用双线性插值来变形图像。由于这种通过空间变换器网络的网格采样是可微的，因此我们的深度学习模型可以通过优化过程中的反向传播误差来训练。

C. 多尺度图像配准(Mutiscale Image Registration)

虽然所提出的CycleMmorph在各种图像域上提供了强大的变形，但深度神经网络应该使用GPU进行训练，其瓶颈是有限的内存。特别是，这是3D图像配准的问题，例如在多个时间点对肝脏进行对比增强CT配准。

由于CycleMmorph不仅可以应用于全尺寸图像，还可以应用于下采样图像和局部补丁，因此可以通过多尺度图像配准方法（即全局配准后局部配准）来解决内存限制问题。

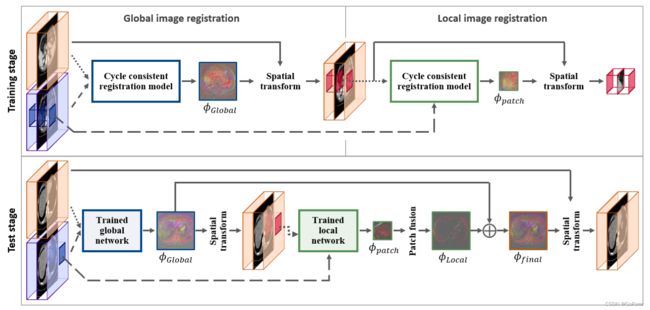
图4显示了所提出的多尺度配准方法中训练和测试阶段的示意流程图。更多详情如下。

图4.大规模图像的多尺度配准方法的流程图。上部说明了全局和局部图像配准的训练阶段的流程。下半部分显示了使用针对给定运动图像和固定图像的训练的全局和局部配准网络的测试阶段的流程。短虚线和长虚线分别指示运动图像和固定图像。

1） 训练阶段：在训练阶段，全局和局部配准网络分别通过建议的周期一致模型进行训练。特别地，首先在子采样图像对上训练全局图像配准模型，然后通过对变形场进行上采样来获得全分辨率变形图像。然后，局部图像配准模型为对从来自全局配准的变形图像和原始固定图像提取的补丁进行训练。

2） 测试阶段：尽管全局和局部配准网络是单独训练的，但由于每个阶段内插误差的累积，具有两个配准网络的运动图像的连续变形可能会降低配准精度。因此，不需要对运动图像进行两次变形，而是连续应用训练的全局和局部网络来估计每个尺度上的变形场，并且使用细化的变形场仅执行一次运动图像的最终变形（见图4）。

具体而言，给定由运动图像和固定图像组成的新输入对，训练的全局配准网络生成中间变形图像和相应的变形向量场。然后，局部配准网络获取从变形图像和固定图像中提取的面片的输入，从而可以为每个面片生成变形场。通过融合由局部网络生成的所有面片的变形场，获得了精细尺度上的整个变形场。然后，通过添加全局和局部配准场+，可以估计最终的变形向量场。利用该和空间变换器，运动图像最终变形一次，以与固定目标图像对齐。

 因此，最终变形图像可以具有与原始运动图像的分辨率类似的分辨率，而不会累积插值误差。

四、 方法

为了证明所提出方法的灵活性和改进的性能，文章使用来自不同应用领域的图像进行了实验。首先，将文章的方法应用于面部表情图像，以显示2D图像上的配准性能。第二，应用于3D大脑MR配准基准数据集，在该数据集中，单个大脑图像被配准到公共图谱中。最后，使用肝脏CECT数据集的一个极具挑战性的配准问题来验证文章的方法，在该问题中，应估计来自大3D体积的广泛变形，以进行多相对比增强模式分析。

A.数据集

1） 面部表情图像：2D面部表情图像从Radboud Faces数据库（RaFD）中获得。为每个67个对象提供了八个不同的面部表情图像；中立、愤怒、轻蔑、厌恶、恐惧、快乐、悲伤和惊讶。该数据集还为所有面部表情图像提供三个不同的注视方向，从而总共有1608个图像。文章将数据集分为53、7和7组，分别用于训练、验证和测试图像，并使用凝视同一方向的所有人脸图像。将所有图像裁剪为640×640，并将其调整为128×128。

2） 脑部MRI：对于脑部MR图像配准任务，文章使用OASIS-3数据集。这提供了1249张T1加权3D大脑MR图像和通过FreeSurfer生成的相应体积分割结果。具体来说，首先使用标准预处理步骤对数据进行预处理：用1各向同性体素将所有扫描重新采样到256×256×256网格，仿射空间归一化，以及大脑提取。然后，将图像裁剪为160×192×224，并除以255。将1027次扫描进行网络训练，93次扫描进行验证，129次扫描进行测试数据。

3） 多期肝脏CT：多期肝脏扫描由韩国首尔Asan医疗中心提供。每一次扫描都是从具有肝脏HCC危险因素的患者身上采集的。该扫描是4D肝脏CT，在造影剂注射前后的四个阶段（未增强、动脉、门静脉和180-s延迟阶段）的3D体积。数据的分辨率为512×512×depth，其中depth是每个CT图像的切片数，切片厚度为5mm。文章使用555次扫描训练了图像配准网络，并在50次测试扫描上评估了提出的方法。

 这里，由于多相图像的深度可能因其扫描时间、图像覆盖范围和图像视野的不同而有所不同，因此通过由改进的U-Net训练的分割网络提取包括肝脏在内的切片，而不是将数据重新采样成相同的图像大小。然后，为了将沿通道方向的移动和固定图像堆叠为网络输入，文章对上下体积进行了零填充，以使切片数量如图5所示。这允许输入图像具有与原始图像相同的特征，而不会在肝脏区域中丢失任何信息。我们用每个体积的最大值归一化图像。

 图5.在腹部CT图像中提取包括肝脏在内的切片的过程图示。

B.实施详细信息

使用pyTorch库在Python中实现了所提出的可变形配准方法。人脸和医学图像配准任务的具体实现细节如下。

1） 2D面部表情图像配准：对于面部图像配准，采用了2D U-Net，它将2D图像作为运动图像和固定图像的输入，并在宽度和高度方向上生成变形场。在网络的训练中，文章使用学习率为和批量大小1的Adam优化算法。将超参数设置为α=0.5、β=1和λ=1。通过随机垂直翻转来增强数据，并使用单个GPU NVIDIA GeForce GTX 1080 Ti对模型进行了20个时期的训练。对于输入，文章将RGB图像转换为灰度级，但要获得具有RGB通道的变形图像，文章在测试阶段将灰度图像的相同变形场应用于每个RGB通道。

2） 3D医学图像配准：为了利用3D医学图像配准任务评估所提出的模型，我们采用了3D CNN，该3D CNN获取3D体积并生成宽度、高度和深度方向的位移矢量场。文章使用VoxelMorph-1作为基线网络，因此文章的深度学习模型没有周期损失和同一损失相当于VoxelMorph-1。该网络架构由编码器、解码器及其它连接组成，类似于U-Net。在这里，由于训练3D CNN的内存使用率很高，我们将批量大小设置为1。为了增加数据，文章对每个训练体积对采用了90度的随机水平和垂直翻转和旋转，以在不过度拟合的情况下提高配准性能。对于脑部MRI配准，文章将超参数设置为α=0.1、β=0.5和λ=1。为了训练网络，文章应用Adam动量优化算法，学习率为。使用单个GPU NVIDIA Titan RTX，文章对模型进行了30个时期的训练。在这里，即使大脑配准任务适合GPU内存，文章也测试了提出的的多尺度配准方法，以与现有的配准方法进行比较。为了在多尺度方法中训练局部配准模型，从全局变形图像和大小为p×p×p的固定图像中提取了patchs，其中在实验中p＝64，并且在推断阶段，通过将块重叠来获得局部配准场。将学习率设置为，并对模型进行了70个时期的训练。

对于多相肝脏CT图像配准，文章采用多尺度配准方法来解决GPU内存的限制。对于全局配准模型，对输入图像对进行了从512×512×depth到128×128×depth的二次采样，以适应GPU内存大小，但在推断阶段，通过上采样获得了全分辨率变形场。此外，多尺度方法中的局部配准模型的训练方法与上述脑配准方法相同。使用单个GPU NVIDIA GeForce GTX 1080 Ti，通过Adam优化以的学习率分别训练了50和30个时期的全局和局部配准网络。将超参数设置为α=0.1、β=1和λ=1。

C.评估

为了定量验证所提出的方法，文章评估了变形图像和固定图像之间的配准精度。首先，通过测量变形场φ的规律性，使用通用的评估标准。这可以通过计算φ上雅可比矩阵行列式中非正值的百分比来实现，其可由下式定义：

其中v表示体素位置，|·|是矩阵的行列式。根据雅可比矩阵的性质，当雅可比矩阵行列式具有所有正值时，变形是微分同胚的，因此负雅可比的百分比表示配准与微分配准有多大不同。

每个数据集的额外定量评估标准取决于每个应用：面部表情图像数据集具有变形图像的地面真实标签；脑MR数据集具有若干脑结构的分割图；肝脏CT数据集具有解剖标志点。因此，文章对每个数据集采用了不同的评估方法。详情如下。

1） 面部表情图像配准分析：在面部表情图像配准任务中，对同一方向的同一个人的不同面部表情图像进行变形。因此，所有变形图像都有地面真值标签，因此通过变形图像和固定目标图像之间的归一化均方误差（NMSE）和结构相似性（SSIM）来评估人脸图像配准的结果。对于所有成对的面部表情图像，我们对分数进行了平均，以进行定量分析。

2） 脑部MRI配准分析：由于我们使用的脑部MR数据集具有脑部解剖结构的分割标签，因此文章使用变形分割图和固定图集分割标签之间的Dice评分来评估配准性能，其可计算为：

其中TP、FP和FN是真位置、假位置和假消极区域的像素数。在分割的解剖结构中，文章提取了30个通常由体积中超过100个像素组成的结构。为了获得配准图像的分割图，使用从原始图像和图集之间的配准网络计算的变形场来变形运动图像的原始分割图。

3） 肝脏CT配准分析：为了定量评估肝脏CT配准，文章计算了50次测试CT扫描的轴向门叶图像上肝脏和相邻器官中20个解剖和病理点的目标配准误差（TRE），这些图像由放射科医生标记。TRE可通过平均值计算欧几里得距离如下：

其中N是界标点的数量，和分别是运动图像A和固定图像B中的第i个界标坐标向量。此外，文章还测量了肝癌大小与癌区大小的差异，以验证其在肿瘤诊断方面的表现。

4） 比较方法：为了验证所提出方法的改进性能，文章采用了几种比较方法，这些方法显示了图像配准中最先进的性能：Elastix、高级归一化工具（ANTs）的SyN、VoxelMorph和MS DIRNet。除了经典方法Elastix和ANTs，文章使用中提出的VoxelMorph-1作为基线网络，并使用相同的参数进行公平比较。由于MS DIRNet是解决GPU内存问题的代表性多尺度方法之一，文章使用MS DIRNet作为基线方法来比较我们对CycleMorph的多尺度实现。

五、 实验结果

A. 人脸表情图像配准

1） 定性评估：图6显示了对男性、女性和儿童的各种面部表情照片的2D图像配准结果的视觉比较。我们变形源图像以跟随目标图像。可以观察到，所提出的方法使源图像变形得更相似与VoxelMorph相比，特别是在眼睛和嘴巴区域。在大多数数据集中，发现与VoxelMorph相比，提出的CycleMmorph提供了显著高质量的图像配准结果。

为了明确分析周期一致性对保持微分性的影响，文章还进行了研究在变形场上，变形的图像是否保持拓扑并可以返回到其原始图像。为了将变形图像反向配准到原始图像中，将前向变形图像设置为新的源图像，将原始源图像设置为目标图像，并应用相同的配准网络。图7（a）（b）底部行中的图说明了反向图像配准的视觉比较结果。结果表明，所提出的方法提供了可以反转为原始图像的变形图像，而VoxelMorph的变形图像不能反转。

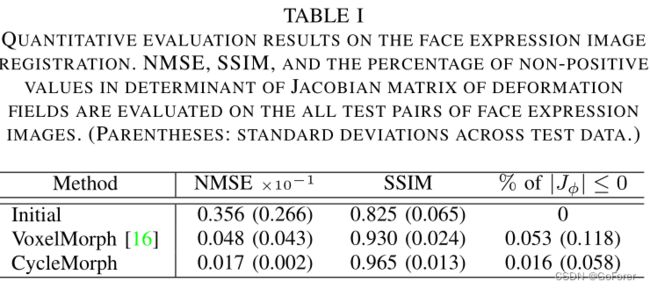
2） 定量评估：表I包括比较方法（VoxelMorph）和文章提出的方法的定量评估结果，这表明CycleMmorph在所有指标上都显著优于VoxelMorph。为了有效地比较图像配准的性能，文章在配准之前计算了源图像和目标图像的评估分数。通过比较，发现与初始值相比，提出CycleMmorph降低了0.034的NMSE，增加了0.140的SSIM。此外，CycleMmorph在雅可比行列式的度量上比VoxelMorph提高了0.037%。

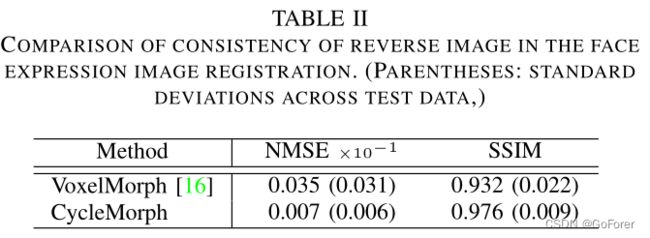
此外，表II显示了重新变形图像（图7（a）（b）底部行中的图形）与其原始运动图像之间的NMSE和SSIM。与VoxelMorph相比，文章的方法得到的反转图像与原始图像非常相似，具有更低的NMSE和更高的SSIM。因此，我们可以确认该方法在生成变形场方面发挥了重要作用，该变形场保证了输入图像的拓扑保持，同时减少了折叠问题。

B. 脑部MR图像配准

1） 定性评估：基于图谱的大脑MR图像配准结果如图8所示。所提出的CycleMorph方法为每对运动源和固定目标图像精确变形图像，这可以通过几个大脑结构的分割边界来具体验证。此外，由于周期约束，可以确认图像配准是由没有奇点的平滑变形场执行的。

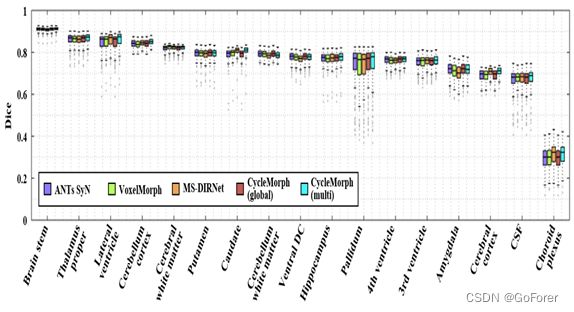
2） 定量评估：为了评估所提出的基于图谱的脑MR图像配准方法，文章将该方法与几种比较方法进行了比较：ANTs用于传统方法，VoxelMorph和MS DIRNet用于基于深度学习的全局和多尺度方法。图9显示了测试扫描中评估解剖结构的Dice评分。左右脑结构的得分平均为一个得分。对于所有结构，CycleMorph模型在全局配准中的得分都高于VoxelMorph，在多尺度配准中的分数高于MS DIRNet。特别是，在脑干、丘脑、海马、苍白球和第四脑室等一些结构上，文章的全局和多尺度CycleMorph模型比比较方法表现更好。

 图9.脑解剖结构变形分割图上的Dice评分，用于基于图谱的脑MR图像配准的定量比较。

表III显示了所有结构和扫描的平均Dice分数、雅可比行列式中非正值的百分比和运行时间的定量评估结果。对于全局配准，与VoxelMorph相比，所提出的CycleMorph显示出更高的Dice度量，非正Jacobian行列式的百分比更少。因此，可以确认CycleMmorph强制执行不同的变形，并执行有效和准确的3D图像配准。这些结果类似地显示在多尺度配准方法与MS DIRNet和文章的方法的比较中。然而，在MS DIRNet和文章的方法中，雅可比行列式指数随多尺度配准而变差。

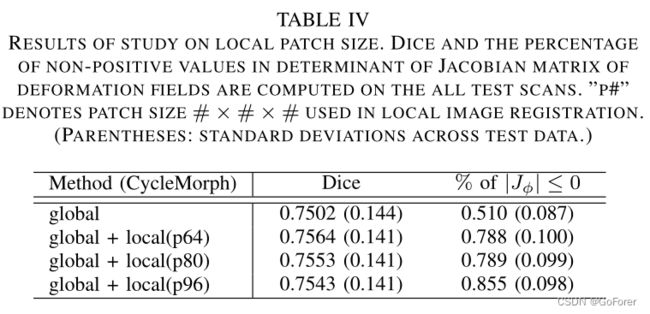
3） 局部path大小研究：由于我们的方法在局部图像配准中的补丁大小可以是不同的，因此我们还研究了所提出的模型中局部补丁大小的影响。如表IV所示，将全局配准结果设置为基线，并使用不同的补丁大小进行了局部配准实验。

当将结果与Dice分数和Jacobian行列式进行比较时，所有多尺度方法都改进了Dice分数的全局配准结果，但在Jacobian行列式中生成了具有更多非正值的变形场。此外，当贴片尺寸较小时，可以观察到解剖结构的Dice评分结果趋于较高，并且变形规律性也较好，折叠问题较少。根据这些结果，在实验中提取了64×64×64的补丁。

C.多期肝脏CT图像配准

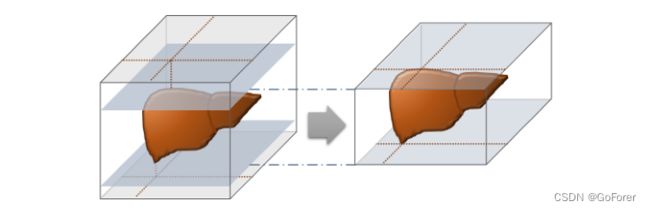
1） 定性评估：图10和图11说明了CycleMorph的多尺度配准结果。具体而言，图10显示，所提出的方法在具有不同对比度的所有多相3D图像上提供了具有平滑变形矢量场的精确配准结果。此外图11显示，多尺度配准性能优于全局配准结果，这在变形图像和目标图像之间的差异图像中得到了很好的可视化。从这个结果中，可以确认，全局配准倾向于使源图像的整个形状变形以适合固定的目标图像，而局部配准提供局部区域变形。

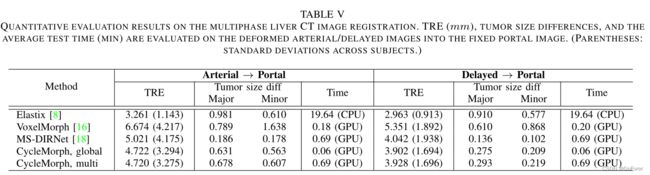
2） 定量评估：文章对动脉期/延迟期到门静脉期的变形图像的配准结果进行了定量评估，这在临床实践中经常被用作标准。这里，由于未增强阶段的图像很难获得界标点，没有计算未增强阶段图像的评估度量。表V显示了使用各种比较方法进行3D图像配准的平均TRE、肿瘤大小差异和运行时间的结果。 

具体地说，可以观察到，与VoxelMorph和MS DIRNet的现有深度学习方法相比，所提出的方法实现了配准性能的显著提高，而所提出方法的TRE略高于Elastix。特别是，变形图像和来自提出方法的门静脉期图像之间的肿瘤大小差异小于比较方法，这证实了所提出的方法即使在小的癌症区域上也提供了最精确的变形。尽管MS DIRNet显示了比较中最小的肿瘤大小差异，但可以确认，文章的CycleMorph的配准质量比MSDIRNet好得多，如图11所示。此外，当计算图像配准的运行时，基于深度学习的使用一个GPU，模型只需不到1分钟，而Elastix的传统方法大约需要20分钟。这里，所提出的方法的全局配准仅需约4秒，多尺度配准的总运行时间为41秒。

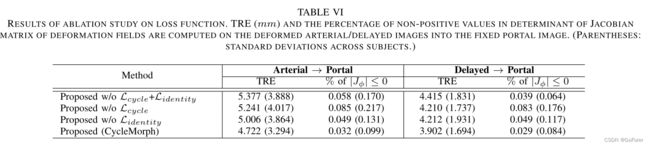
 3） 损失函数消融研究：为了验证文章设计的损失函数中周期约束的影响，还通过排除周期损失和/或同一性损失对肝脏CT数据进行了消融研究。在本研究中，文章分析了具有相同训练和测试程序的全局图像配准结果，以进行公平比较。表VI显示了变形场上雅可比矩阵行列式中非正值的百分比以及TRE，这表明根据损失函数的配准性能变化是显著的。仅通过配准损失训练的网络，即没有Lcycle和Lidnentity，使图像变形的方法中误差最大。周期和同一性损失功能都提高了配准的准确性。

另一方面，雅可比矩阵的评估度量强调了循环一致性的影响。具体而言，与具有循环约束的所提出的方法相比，不具有循环损失的所提出方法产生的变形场具有更多的雅可比矩阵行列式的非正体素。这里，与其他方法相比，仅具有配准损失的方法具有更小的雅可比行列式非正值百分比的原因是因为网络提供了在大规模图像上几乎不变形的配准场，这可以用TRE值来确认。相比之下，由于周期损失，所提出的方法不易出现折叠问题，并增强了3D图像配准的拓扑保持。

六、 结论

本文中作者提出了一种用于无监督可变形图像配准方法的循环一致深度学习模型CycleMmorph。CycleMorph在一对图像之间施加循环一致性。一旦对网络进行了训练，单个网络就可以用任何一对新数据提供精确的图像配准。CycleMorph也被扩展到多尺度方法来处理大体积配准问题。使用各种图像数据集的实验证实，CycleMorph为任何图像对提供了拓扑保持的图像变形，并提供了显著的性能改进。

注：仅作为自己的学习记录，无其他目的。