卡尔曼滤波与粒子滤波比较

两种滤波的重要性不必赘述，在自动控制领域的无异于牛顿的三大定律，都是贝叶斯滤波的不同表述和推广。

对卡尔曼滤波，[1]是状态估计的经典教材，它的第一章从简单的例子出发，深入浅出地解释什么是滤波，为什么卡尔曼滤波是最优的；粒子滤波强烈推荐[3]， 这篇论文详细的介绍了例子滤波的发展历程和各类变种，最有用的是有人根据这篇论文实现了代码[3]；[4]是博士论文的节选，从编程的角度介绍了粒子滤波如何应用到移动机器人定位。

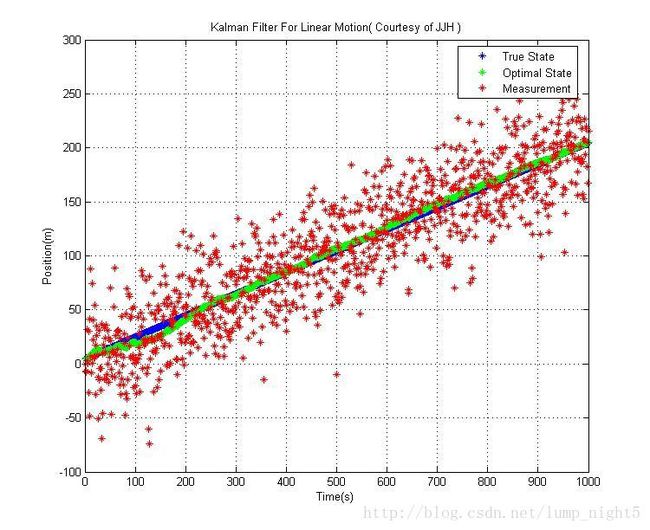
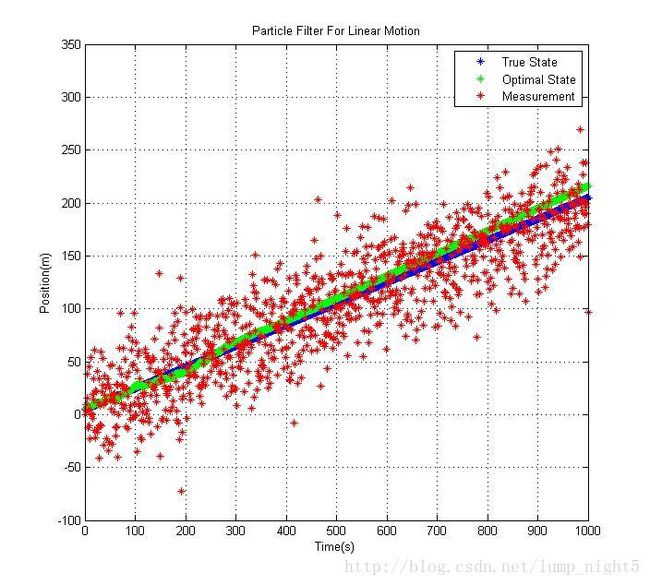
采用简单的线性模型，[ x vx y vy]'为状态变量，观测量是位置[ x y ]'，跟踪位置x的结果如下，注意到KF要比PF的跟踪效果好（PF的RMS大概是KF的四倍），这是因为从误差最小的原则来讲，Kalman Filter是最优的。

源代码：

Kalman Filter

%% Lucas Wang, XJTU, 2014.09.18, and I appreciate for the protype code offering by my girl friend, I love her very much~
clc;clear all;close all;
%% parameter of state equation
T = 0.01;
F=[1 T 0 0;
    0 1 0 0;
    0 0 1 T;
    0 0 0 1];
G=[T^2/2 0;
    T 0;
    0 T^2/2;
    0 T];
Q = diag( [0.04 0.09] );
%parameter of measurement equation
H=[1 0 0 0;
    0 0 1 0];
R=diag([900 900]);

% Initialization of state estimators
x0=[5 20 6 18]';
% P0=diag( [400 64 625 49] );
L = 30;
P0 = diag( [ L L L L ]);
StateDim = size( F, 1 );
ObvDim   = size( H, 1 );
% reset the random number generator to a different state each time
randn('state',sum(100*clock));


% %% Kalman Filter.
x_True    = [ x0 ];
x_Noise   = [ x0 ];
x_Predict = [ x0 ];
x_Est     = [ x0 ];
z_True    = [];
z_Noise   = [];
P_Predict = [];
P_Est( :, :, 1 ) = P0;
MaxIter = 1000;
for k = 2 : 1 : MaxIter
    % ground truth.
    x_True( :, k ) = F * x_True( :, k - 1 ); 
    Z_True( :, k ) = H * x_True(:, k );
    % Add noise.
    Wk = G * sqrtm(Q) * randn( 2, 1 );
    x_Noise( :, k ) = F * x_Noise( :, k - 1 ) + Wk; 
    Vk = sqrtm(R)*randn( 2, 1 );
    z_Noise( :, k ) = H * x_Noise( :, k ) + Vk;
    % Predicate.
    x_Predict( :, k ) = F * x_Est( :, k - 1 );
    P_Predict( :, :, k ) = F * P_Est( :, :, k - 1 ) * F' + G * Q * G';
    % Update.
    y(:, k ) = z_Noise( :, k ) - H * x_Predict( :, k );
    S(:, :, k ) = H * P_Predict( :, :, k ) * H' + R;
    K( :, :, k ) = P_Predict( :, :, k ) * H' * inv( S( :, :, k ) );
    x_Est(:, k ) = x_Predict( :, k ) + K( :, :, k ) * y( :, k );
    P_Est( :, :, k ) = ( eye(StateDim) - K( :, :, k ) * H ) * P_Predict( :, :, k );
end
RMS = mean( ( x_Est - x_True ).^2, 2 )
%% Visualize.
figure(2);
plot( x_True( 1, : ), 'b*' );
hold on;plot( x_Est( 1, : ), 'g*' );
hold on; plot( z_Noise( 1, : ), 'r*' );
legend('True State', 'Optimal State', 'Measurement' );
title( ' Kalman Filter For Linear Motion( Courtesy of JJH ) ');
xlabel('Time(s)');ylabel( 'Position(m)' );
grid on;

Particle Filter, 其中的particle_filter()取自[3].

%% Lucas Wang, XJTU, 2014.09.18
clc;clear all;close all;
% parameter of state equation
T = 0.01;
F=[1 T 0 0;
    0 1 0 0;
    0 0 1 T;
    0 0 0 1];
G=[T^2/2 0;
    T 0;
    0 T^2/2;
    0 T];
Q = diag( [0.04 0.09] );
%parameter of measurement equation
H=[1 0 0 0;
    0 0 1 0];
R=diag([900 900]);

% Initialization of state estimators
x0=[5 20 6 18]';
% P0=diag( [400 64 625 49] );
L = 30;
P0 = diag( [ L L L L ]);
StateDim = size( F, 1 );
ObvDim   = size( H, 1 );
% %% Kalman Filter.
x_True    = [ x0 ];
x_Noise   = [ x0 ];
z_True    = [];
z_Noise   = [];
%% Particle Filter.
TotalTime = 1000;
nx = StateDim;
% function description.
sys = @(k, xkm1, uk) F * xkm1 + uk;
obs = @(k, zkm1, vk) H * zkm1 + vk;
p_yk_given_xk = @( k, yk, xk ) mvnpdf( yk - H * xk, zeros( ObvDim, 1 ), R ); % associate with weight calculate.
gen_x0 = @(x) mvnrnd( x0, P0 );
gen_sys_noise = @(u) ( mvnrnd( zeros( StateDim, 1 ), G * Q * G' ) )';
gen_obs_noise = @(u) ( mvnrnd( zeros( ObvDim,   1 ), R ) )';
% initialization of particle filter.
pf.k               = 1;                   % initial iteration number
pf.Ns              = 100;                 % number of particles
pf.w               = zeros(pf.Ns, TotalTime);     % weights
pf.particles       = zeros( nx, pf.Ns, TotalTime ); % particles
pf.gen_x0          = gen_x0;              % function for sampling from initial pdf p_x0
pf.p_yk_given_xk   = p_yk_given_xk;       % function of the observation likelihood PDF p(y[k] | x[k])
pf.gen_sys_noise   = gen_sys_noise;       % function for generating system noise

% Estimate state
for k = 2:TotalTime
   fprintf( 'Iteration = %d/%d\n',k, TotalTime ); 
    x_True( :, k ) = sys( k, x_True(:, k - 1 ), 0 ); 
    Z_True( :, k ) = obs( k, x_True(:, k - 1 ), 0 );
    % Add noise.
    Wk = gen_sys_noise();
    x_Noise( :, k ) = sys( k, x_True(:, k - 1 ), Wk ); 
    Vk = gen_obs_noise();
    z_Noise( :, k ) = obs( k, x_True(:, k - 1 ), Vk );
   % state estimation
   pf.k = k;
   %[xh(:,k), pf] = particle_filter(sys, y(:,k), pf, 'multinomial_resampling');
   [xh(:,k), pf] = particle_filter( sys, z_Noise( :, k ), pf, 'systematic_resampling' );   
 
   % filtered observation
   yh(:,k) = obs(k, xh(:,k), 0);
end
RMS = mean( ( xh - x_True ).^2, 2 )

figure;
plot( x_True( 1, : ), 'b*' );
hold on;plot( xh( 1, : ), 'g*' );
hold on; plot( z_Noise( 1, : ), 'r*' );
legend('True State', 'Optimal State', 'Measurement' );
title( 'Particle Filter For Linear Motion' );xlabel('Time(s)'); ylabel('Position(m)');grid on;

参考文献：

[1] Maybeck, Stochastic Models, Estimation, and Control.

[2] M. Sanjeev Arulampalam, A turtorial on Particle Filters for online Nonlinear/Non-Gaussian Bayesian Tracking[J], IEEE Transactions on Signal Processing, 2002.

[3] 点击打开链接

[4] Ioannis M. Rekleitis, A Particle Filter Tutorial for Mobile Robot Localization, Technical Report of Centre for Intelligent Machines, McGill University, 2004.

ps: 特别感谢韩姑娘在卡尔曼滤波上对我的帮助，和她的讨论让我对KF的理解更加深刻，而且Kalman Filter部分的代码也是她提供的。