INS/GNSS组合导航（四）卡尔曼滤波比较之KF、EKF、UKF

1.摘要

卡尔曼滤波自1960年代发表至今，在各个时间序列估计领域尤其是位置估计、惯性导航等得到了广泛的应用，后续逐渐演化出EKF、UKF以及PF，其中PF本文不作展开对比，重点对比KF、EKF与UKF的差异及演化来历。

2.卡尔曼滤波由来

卡尔曼滤波（Kalman Filter）是一种高效的自回归滤波器，它能在诸多不确定性情况的组合信息中估计动态系统的状态，是一种强大的、通用性极强的工具。由鲁道夫.E.卡尔曼于1961年前后首次提出，并首先应用于阿波罗计划的轨道预测。

3.卡尔曼滤波器原理

卡尔曼滤波模型假设k时刻的真实状态是从（k − 1）时刻的状态演化而来，符合下式：

其中

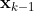• 是作用在上的状态变换模型（变换矩阵）。
• 是作用在控制器向量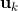上的输入－控制模型。
• 是过程噪声，并假定其符合均值为零，协方差矩阵为的多元正态分布。

时刻k，对真实状态 的一个测量满足下式：

其中是观测模型，它把真实状态空间映射成观测空间，是观测噪声，其均值为零，协方差矩阵为,且服从正态分布。

初始状态以及每一时刻的噪声都认为是互相独立的，即协方差矩阵非对角元素全部为0。

实际上，很多真实世界的动态系统都并不确切的符合这个模型；但由于卡尔曼滤波器被设计在有噪声的情况下工作，一个近似的符合已经可以使这个滤波器非常有用了，实际应用发现，对于并不完全符合上述模型的动态系统也能得到较好的近似效果。更多其它更复杂的卡尔曼滤波器的变种，在下边讨论中会有具体描述。

4.扩展卡尔曼滤波（EKF）、无迹卡尔曼滤波(UKF)

4.1 直观差异

对于KF、EKF、UKF的主要差异，通俗一点说，主要如下：

卡尔曼滤波器 KF 是一种用作最小二乘误差优化器的滤波器，为了使其工作，在滤波器内部考虑的系统必须是线性的,即基于线性系统的前提假设。

为了使用KF对非线性系统进行状态估计或参数估计，一种可能的方法是围绕其当前状态对正在研究的系统进行线性化，并强制滤波器使用系统的这个线性化版本作为模型. 这是Extended Kalman Filter，或简称为EKF。

然而，由于EKF 不是很稳定，而且很多时候，当它确实收敛到“正确”解时，其收敛过程会非常缓慢。为了改进这个滤波器的固有不足，一些作者开始使用 Unscented Transformation，而不是使用线性化来预测被研究系统的行为。因此，具有 Unscented 变换（无迹变换）的 Kalman 滤波器称为 Unscented Kalman Filter，或简称为 UKF。

与 EKF 相比，UKF具有一些优势，因为 Unscented 变换在某种程度上比线性化更好地描述了非线性系统，因此该滤波器更迅速地收敛到正确的解。而使用 EKF，这个滤波器可能会变得不稳定，结果可能会出现偏差。

核心差异总结如下：
KF：    线性化假设，求解线性系统，对应的是线性模型
EKF：  求解对象是非线性系统，通过Taylor展开式，舍去高阶项，基于线性化思想来近似线性化
UKF：  采用线性化近似很多高度非线性系统不合时宜，基于无迹变换，求解得到高斯分布来规避了线性化的行为，UKF的实现具体可分为以下几个步骤：
        a) Compute a set of sigma points

        b) Each sigma points has a weight

        c) Transform the point through the nonlinear function

        d) Compute a Gaussian from weighted points

KF、EKF、UKF比较

模型	适用对象	求解方法	计算复杂度/计算速度
KF	线性系统、线性模型	直接求解	容易/快
EKF	一般非线性系统	Taylor展开式	一般/略慢于KF
UKF	高度非线性系统	无迹变换、高斯分布	复杂/略慢于EKF

4.2 算法差异

4.2.1 KF与EKF的算法差异

对于KF，本质上来说，它是贝叶斯滤波器的一个特例，即这个滤波器是动力学模型和测量模型的一个线性组合。

 

 

 通过上述对比可知，KF模型的状态转移矩阵具有线性化特点，体现在系数矩阵,

而对于EKF模型来说，状态转移对应下一时刻的状态量是上一时刻的非线性函数，不能直接得到，需对采用一阶Taylor系列展开式来近似。

4.2.2 EKF 与UKF的算法差异

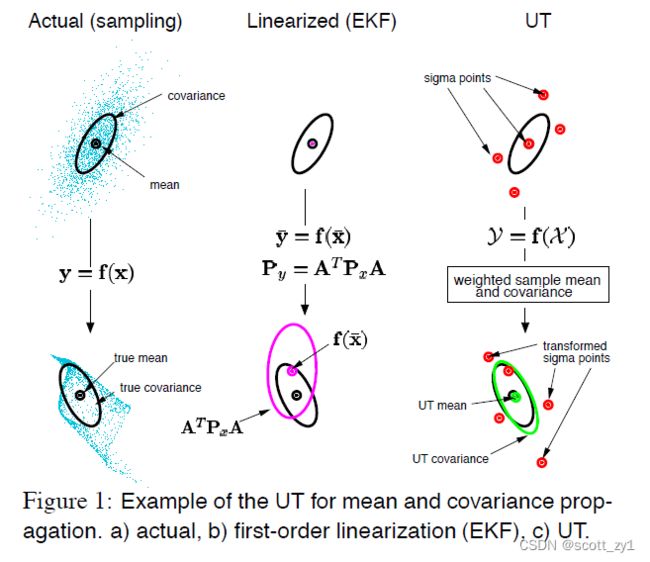
上述EKF中通过非线性函数的一阶Taylor展开式实现线性化，而在UKF则不再采用这种简单的一阶线性化，原因在于对于高度非线性系统，这种舍去二阶以上的线性化处理并不合适，那么从EKF到UKF，最终使得效果好于EKF的直觉在哪里呢？具体可见如下的对比。 

由上可知，在UKF中，不再使用函数的线性近似，而是直接使用了函数本身，但是对函数的自变量也就是数据点的协方差进行近似。直观对比EKF与UKF在算法实现上的差异如下: 

 对于UKF的均值与协方差的更新过程详细步骤如下：

上述详细算法步骤第12步对应的推导过程如下：

 

UKF vs. EKF

—— Same results as EKF for linear models
——  Better approximation than EKF for non-linear models

—— Differences often “somewhat small”
—— No Jacobians needed for the UKF
—— Same complexity class
—— Slightly slower than the EKF
—— Still requires Gaussian distributions

4.2.3总结 KF/EKF、UKF算法实现差异

5. 完整推导

Kalman-Filters （KF）

Extended-Kalman-Filters（EKF）

Unscented-Kalman-Filters（UKF）

Particle-Filters（PF）

6. 参考文献

1.Applied Mathematics in Integrated Navigation Systems 3rd-AIAA

2.Strapdown Inertial Navigation Technology,2nd.

3.Principles of GNSS, Inertial, and Multisensor Integrated Navigation Systems,(2008)

4.Optimal Estimation of Dynamic Systems, Second Edition 

5. A New Extension of the Kalman Filter to Nonlinear Systems

6. Probabilistic Robotics

7.The Unscented Kalman Filter for Nonlinear Estimation