python图像处理笔记-十二-图像聚类
python图像处理笔记-十二-图像聚类
学习内容
这一章主要在学习的是聚类算法以及其在图像算法中的应用,主要学习的聚类方法有:
- KMeans
- 层次聚类
- 谱聚类
并将使用他们对字母数据及进行聚类处理,以对比效果。
聚类是什么?
有n个点,把这n个点通过某种方法分成k类就是聚类算法在做的事情,聚类做的越好,分出来的k类的类与类之间差异越明显,同一个类中的差异也越不明显。
K-means
聚类思想:
K-means需要给出最终簇的数量k。它的核心思路是:从某个状态开始,通过不断的迭代来更新中心点的位置,来让分类效果尽可能最优。其实质是在优化下面的函数,使其尽可能地小:
V = Σ i = 1 k Σ x j ∈ c i ( x j − μ i ) 2 V = \Sigma_{i=1}^k \Sigma _{x_j \in c_i}(x_j-\mu_i)^2 V=Σi=1kΣxj∈ci(xj−μi)2
这种方法最大的问题在于,需要手动选择最终的簇的数量k,如果选择的簇的数量过大或过小,都会使结果很差。
因为这个我之前已经学过了,而且已经用烂了,就不介绍详细方法了,大家可以上网去查,一抓一大把。
聚类的实现:
为了和书中的代码同步,所以我也学着去使用Scipy中的聚类包。如果你想尝试一下别的,可以去试一下sklearn中的聚类包,它同样非常好用。
这里我们模仿书上的例子,对手写字体数据集中的数据进行聚类,大体的过程如下:
- 对数据进行主成分分析
- 对主成分分析后的进行聚类
- 对聚类结果进行显示
代码如下:
import osimport pickleimport numpy as npfrom PIL import Imageimport pylab as plfrom PCV.tools import pcafrom scipy.cluster.vq import *# 获取字母数据集下的图片文件名,并且保存在列表中imlist = os.listdir('a_selected_thumbs/')imnbr= len(imlist)with open('font_pca_modes.pkl', 'rb') as f: immean = pickle.load(f) V = pickle.load(f)# 创建矩阵,存储所有拉成一组形式后的图像immatrix = np.array([np.array(Image.open('a_selected_thumbs/'+im)).flatten()for im in imlist],'f')# 投影到前40 个主成分上immean = immean.flatten()projected = np.array([np.dot(V[:30],immatrix[i]-immean) for i in range(imnbr)])# 进行k-means 聚类projected = whiten(projected)centroids,distortion = kmeans(projected,4)code,distance = vq(projected,centroids)# 绘制聚类簇for k in range(4): ind = np.where(code==k)[0] pl.figure() pl.gray() for i in range(min(len(ind),40)): pl.subplot(4,10,i+1) pl.imshow(immatrix[ind[i]].reshape((25,25))) pl.axis('off') pl.show()projected = np.array([np.dot(V[[0,2]],immatrix[i]-immean) for i in range(imnbr)])from PIL import Image, ImageDraw# 高和宽h,w = 1200,1200# 创建一幅白色背景图img = Image.new('RGB',(w,h),(255,255,255))draw = ImageDraw.Draw(img)# 绘制坐标轴draw.line((0,h/2,w,h/2),fill=(255,0,0))draw.line((w/2,0,w/2,h),fill=(255,0,0))# 缩放以适应坐标系scale = np.abs(projected).max(0)scaled = np.floor(np.array([ (p / scale) * (w/2-20,h/2-20) + (w/2,h/2) for p in projected]))# 粘贴每幅图像的缩略图到白色背景图片for i in range(imnbr): nodeim = Image.open('a_selected_thumbs/'+imlist[i]) nodeim.thumbnail((25,25)) ns = nodeim.size img.paste(nodeim,(int(scaled[i][0]-ns[0]//2),int(scaled[i][1]-ns[1]//2),int(scaled[i][0]+ns[0]//2+1),int(scaled[i][1]+ns[1]//2+1)))img.save('pca_font.jpg')
跑出来的结果如下:
-
在PCA降低维度至30维后的分类结果(我跑的时候40维结果非常差,所以调整为了30维):
[
 ](https://saiyuwang-blog.oss-cn-beijing.aliyuncs.com/Screenshot from 2020-05-03 15-56-02.png)
](https://saiyuwang-blog.oss-cn-beijing.aliyuncs.com/Screenshot from 2020-05-03 15-56-02.png) -
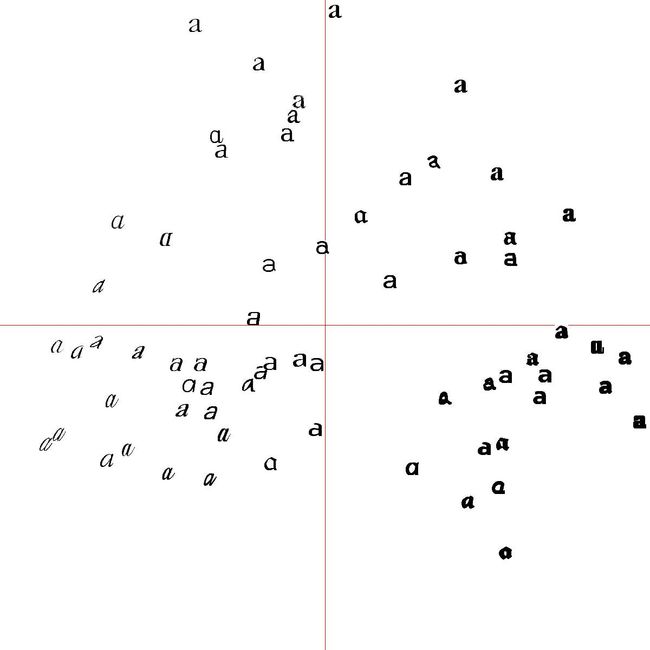
PCA降维至2维后进行显示:
像素聚类
这里我们使用一种非常简单的方法进行聚类,我们不再针对图片本身进行聚类,而是对单张图片中的像素点进行聚类,聚类的依据是图像的RGB三通道信息。我们以某一步长在图像中滑动,每滑动一次记录一次该范围内的均值,将其作为生成的低分辨率图像对应出的像素值,并以该像素值为依据进行聚类。这方法没啥意思,就不实现了,因为想做图像划分的话,这种方法是没用的。
层次聚类
层次聚类的方法如下:
- 在最开始的时候,认为每个数据都是单独的一个簇
- 每次迭代时,合并距离最小的两个簇
- 仅剩下一个簇的时候,停止
这个方法也挺无脑的,不过还是很有用的,实现的时候难点主要在于可视化,我们就不多讲了。
谱聚类
解决的问题
在下面这种情况中(这张图来自于B站白板推理系列):
[ ](https://saiyuwang-blog.oss-cn-beijing.aliyuncs.com/Screenshot from 2020-05-03 16-46-25.png)
](https://saiyuwang-blog.oss-cn-beijing.aliyuncs.com/Screenshot from 2020-05-03 16-46-25.png)
直接使用距离为分类参考依据是的话,分类结果会非常糟糕。
解决流程(粗略)
-
Step1假设数据集中一共有n个点,给定一个n*n的矩阵S,这个矩阵S是用于度量任意两个元素之间的相似性的,当然S是一个对称矩阵,并且S_{ii}=0。
-
Step2构建一个对角矩阵D,该矩阵对角线上元素的值如下:
D i i = Σ j S i j D_{ii}=\Sigma_j S_{ij} Dii=ΣjSij
也就是说,这个D的对角线上的元素的值就等于当前点到其他所有点的距离之和。
-
Step3构建标准化后的拉普拉斯矩阵L
L = D 1 2 S D − 1 2 L = D^{\frac{1}{2}}SD^{-\frac{1}{2}} L=D21SD−21 -
Step4计算L的特征向量,并使用K个最大的他特征值对应的k个特征向量,构建出一个特征向量集(即一个特征矩阵)。
-
Step5将各自对应的特征向量组成的矩阵按行标准化,最终组成维的特征矩阵F
-
Step6对F中的每一行作为一个k_1维的样本,共n个样本,用输入的聚类方法进行聚类,聚类维数为k_2。
-
Step7根据给出的聚类方法进行聚类,得到簇。
代码如下(直接用的sklearn):
from sklearn.cluster import SpectralClusteringfrom sklearn.cluster import KMeansfrom sklearn import metricsimport numpy as npfrom PIL import Imageimport pylab as plimport cv2import osdef getData(dirName): imlist = os.listdir(dirName) features = np.zeros([len(imlist), 512]) for i in range(len(imlist)): im = np.array(Image.open(dirName + imlist[i])) h, edges = np.histogramdd(im.reshape(-1,3),8,normed=True,range=[(0,255),(0,255),(0,255)]) features[i] = h.flatten() return features, imlistif __name__ == "__main__": imDir = '/home/wangsy/Codes/PCVLearning/myCodes/picCluster/flickr-sunsets-small/' LKDir = '/home/wangsy/Codes/PCVLearning/myCodes/picCluster/L+K/' KMDir = '/home/wangsy/Codes/PCVLearning/myCodes/picCluster/KMeans/' X, imNames = getData(imDir) y_pred = SpectralClustering(n_clusters=10).fit_predict(X) for i in range(10): # 把里面的图像都删掉 for j in os.listdir(LKDir+str(i)): os.remove(LKDir+str(i) + '/' + j) # 把原来的文件夹也删了 os.rmdir(LKDir+str(i)) # 在建立个新的 os.mkdir(LKDir+str(i)) ndx = np.where(y_pred == i)[0] for j in ndx: Image.open(imDir + imNames[j]).save(LKDir+str(i)+'/'+str(j) + '.jpg' ) y_pred = KMeans(n_clusters=10).fit_predict(X) for i in range(10): # 把里面的图像都删掉 for j in os.listdir(KMDir+str(i)): os.remove(KMDir+str(i) + '/' + j) # 把原来的文件夹也删了 os.rmdir(KMDir+str(i)) # 在建立个新的 os.mkdir(KMDir+str(i)) ndx = np.where(y_pred == i)[0] for j in ndx: Image.open(imDir + imNames[j]).save(KMDir+str(i)+'/'+str(j) + '.jpg' )
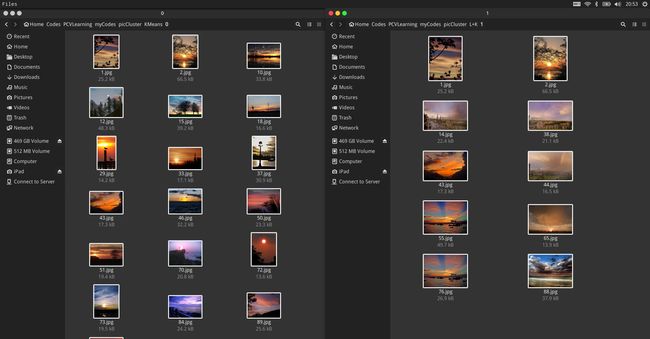
在这段代码中,我们对100副海边的照片提取了直方图,然后对直方图分别使用Kmeans和谱聚类进行聚类分析,结果如下,我们对比图片1所在的分类中,左边的是KMeans分类的结果,右边的是谱聚类分类的结果:
[ ](https://saiyuwang-blog.oss-cn-beijing.aliyuncs.com/Screenshot from 2020-05-03 20-53-01.png)
](https://saiyuwang-blog.oss-cn-beijing.aliyuncs.com/Screenshot from 2020-05-03 20-53-01.png)
可以看出来,谱聚类在该问题上的分类结果更为理想。