医疗图像配准-点云配准总结

近期主要在做一个关于将三维CT影像和点云数据做配准的项目，通过前期调研，业内主要的方法是将CT影像使用MarchingCubes（移动立方体）生成等值面三角网格，然后再使用点云配准的方法。

1、三维图像转三角网格（STL）

三维图像转stl网格，在vtk中已经实现，主要使用MarchingCubes算法，简单而有效，算法介绍详见下面篇博文，对比众多水文，这篇讲的比较明白。
图像数据到网格数据-1——MarchingCubes算法 - 止战 - 博客园原文：http://blog.csdn.net/u013339596/article/details/19167907概述 之前的博文已经完整的介绍了三维图像数据和三角形网格数据。在实际应用中，利用遥https://www.cnblogs.com/zhizhan/p/3987254.html

2.配准工具选择

在配准工具选择中，先后使用了vtk和itk，其内部都包含了icp算法的模块，但都是经典的point-to-point算法，而且只适宜对数据量较少的点进行配准，如果点太多，那么耗时太久，虽然itk官方例子中有可以通过构建距离图的例子加快运算，但通过实际使用，并没有起到很好的加速作用，综合比较之后，最终还是选用点云专门处理库PCL做。

3.PCL配准库基本介绍

PCL配准库中集成了很多针对点云配准的精配准及粗配准方法，主要类如下：

（1）CorrespondenceEstimation类，用来确定两点云中的对应匹配关系。

（2）CorrespondenceRejectorFeatures类，能够实现基于特征匹配的对应点对提取。

（3）SampleConsensusPrerejective类，实现了基于RANSAC方法的对应点对外点去除，用于姿态评估和点云配准中的几何一致性限制，从而保证后续算法的准确和高效。

（4）TransformationEstimation3Point类，实现使用三个匹配点计算两点云变换矩阵。

（5）TransformationFromCorrespondences类，实现三个及以上匹配点间变换矩阵的计算。

（6）TransformationEstimationDQ类和TransformationEstimationDualQuaternion类

实现基于对偶四元数的点云姿态估计。

（7）TransformationEstimationLM类，实现基于对应匹配点对，用Levenberg-Marquardt优化的变换矩阵估计。

（8）TransformationEstimationPointToPlane类，实现基于Levenberg-Marquardt优化的匹配点对间最小点到平面距离的最优变换矩阵计算。

（9）TransformationEstimationPointToPlaneWeighted类，在TransformationEstimationPointToPlane类的基础上加入了对应匹配点的权重，以适应更为复杂场景点云配准任务。

（10）TransformationEstimationPointToPlaneLLS 类，基于线性最小二乘的点到平面距离累计最小化约束，对应点到平面的距离计算加入法向量约束，具体内容参照论文：Linear Least-Squares Optimization for Point-to-Plane ICP surface registration 2014

（11）TransformationEstimationPointToPlaneLLSWeighted类，在TransformationEstimationPointToPlaneLLS 类基础上加入了对应点匹配权重，从而更合理的计算匹配点间变换矩阵。

（12）TransformationEstimationSVD类，使用SVD分解策略完成匹配点对的变换矩阵计算。

（13）TransformationValidationEuclidean类，实现了给定对应匹配的变换，并计算可靠性得分。

（14）IterativeClosestPoint类，实现迭代最近点算法（ICP）。

（15）IterativeClosestPointNonLinear类，ICP算法的变体，后端使用Levenberg-Marquardt作为优化。

（16）GeneralizedIterativeClosestPoint类，ICP算法的变体，实现了一般化的ICP算法，具体参考Generalized-ICP论文。

（17）GeneralizedIterativeClosestPoint6D类，集成了L*a*b*颜色空间到Generalized-ICP算法中。

（18）IterativeClosestPointWithNormals 类，ICP算法的变体，以点到平面的最小距离作为迭代优化对象，实现点云配准。

（19）FPCSInitialAlignment 类，实现《4-points congruent sets for robust pairwise surface registration》中的4PCS算法；

（20）KFPCSInitialAlignment类，实现《Markerless point cloud registration with keypoint-based 4-points congruent sets》中的k4PCS算法。

（21）NormalDistributionsTransform（NDT）类，统计分析点云中法向量分布，来实现点云的转化和配准。具体参考The Three-Dimensional Normal-Distributions Transform an Efficient Representation for Registration（2009）

4.配准方法介绍

4.1采样一致性初始配准算法SAC-IA（Sample Consensus Initial Aligment ）

4.1.1介绍

       采样一致性初始配准算法通常基于特征描述子PFH和FPFH进行配准。

        PFH（Point Feature Histograms）是一种点云特征点的特征描述子，是一种的姿态不变的局部特征，其目标是编码k邻域中的几何特征，关于PFH描述子生成的原理，网上有很多介绍，在此不再赘述，在PCL中PFH经常会生成125维的向量，有些同学可能不太明白这个特征描述子为什么是125维，其实可以这样想，PCL中主要使用经典的PFH描述子k个邻域内两两点之间的四联体（三个角度一个距离）中的三个角度变量（先叫三联体），然后每个角度变量分成五份，我们可以先不要想125维的一维向量，先生成一个具有5*5*5维度的125个小格子的三维直方图，然后每计算一个三联体，在三维直方图中符合的位置加1，然后计算结束之后，摊开，即成为了125维的一维向量。

        FPFH特征描述子，对PFH特征进一步优化升级就得到了快速点特征直方图(FPFH)。其计算过程如下：

（1）为查询点求得它和其k邻域内每个点之间的三个特征元素值，然后统计成一个SPFH；

（2）分别对k邻域中的每个点确定k邻域，按第一步分别形成自己的SPFH；

（3）加权统计生成最终的33维度的特征向量（每个特征维度生成一个直方图，最后连在一起）

        PFH和FPFH的主要区别

        （1）FPFH没有对全互联点Pq的所有邻近点的计算参数进行统计，因此可能漏掉了一些重要的点对，而这些漏掉的点对可能对捕捉查询点周围的几何特征有贡献。

        （2）PFH特征模型是对查询点周围的一个精确的邻域半径内，而FPFH还包括r范围以外2r以内的额外点对。

        （3）因为重新计算权重的方式，FPFH通过结合SFPH的值，重新捕获邻近重要点对的几何信息。

        （4）FPFH的整体复杂性低，FPFH在实际的应用中更为常见。

4.1.2流程

（1）计算PFH或者FPFH特征描述子

（2）SAC配准(配准的采样记录要大于某个阈值，保证采样点具有不同的特征）,使用Huber作为罚函数

（3）进行精配准

4.1.3算法适用范围

粗配准，可以看到该配准方法还是基于局部特征描述子的一种配准方法。在医疗图像软件中基于特征描述子配准方法使用较少，更多的是先人工选择一些特征点，完成粗配准。

 4.1.4参考资料：

（1）PFH和FPFH_xinxiangwangzhi_的博客-CSDN博客

（2）SAC-IA粗配准+ICP精配准_peach_blossom的博客-CSDN博客_sac-ia

4.2 Point to Point ICP算法

4.2.1算法介绍

方法来自论文《A method for registration of 3-D shapes》，网上介绍比较多，在后续项目中也使用了该算法，总体来说效果还可以，主要公式如下：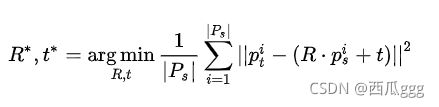

算法主要包含两个步骤

（1）在moving点云在fixed点云中每个点的最近点，在PCL中默认会构建fixed点云KD-tree，所以在配准时，速度比ITK要快很多

（2）基于找到的最近点对，求解最优变换矩阵，在PCL中使用SVD来求解。

4.2.2算法中设置需要设置的变量说明

（1）setMaximumIterations，设置最大迭代次数

（2）setEuclideanFitnessEpsilon，收敛条件，均方误差小于此值就停止迭代。

（3）setTransformtionEpsilon，收敛条件，设置两次变化矩阵之间的差值小于此值就停止迭代。

（4）setMaxCorrespondenaceDistance，设置对应点对之间的最大距离，在步骤1中使用。

4.2.3算法使用中需要注意的问题

（1）ICP算法对初始值很敏感，极容易陷入局部最优解，所以在迭代之前最好设计好初始值。

（2）ICP算法原来上来讲要对moving中找到在fixed点云中的对应点，然后来计算转换矩阵，如果在moving点云中包含了不应该配对的点，这会导致计算误差，这种情况应该避免

（3）ICP的moving点云中最好少用一些平面或者扫描面的点，这种类型点太多的话，对结果影响较大，对于ICP算法来讲，moving点云中尽量包含较多有一定曲率，并且距离较远的点，这样可能会提高精度。

（4）如果moving点云中包含了太多点，可以使用降采样来过滤一些点。

4.2.4适用范围

地球人都知道在精配准中使用.

     

4.3 Point to Plane ICP

4.3.1算法介绍

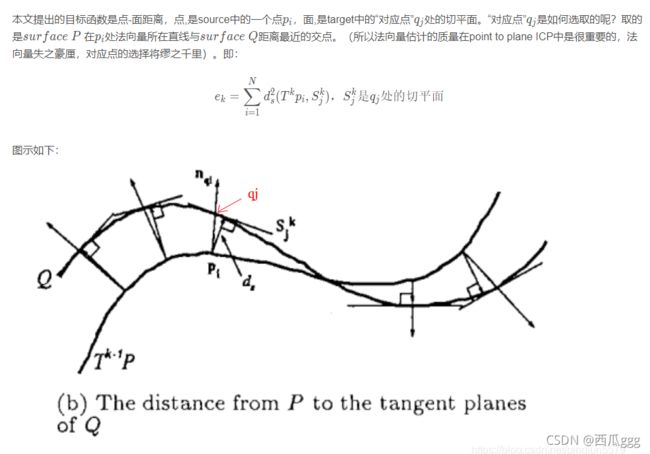
   出自《Object Modeling by Registration of Multiple Range Images》，基本原理如下：

后续由《Linear Least-Squares Optimization for. Point-to-Plane ICP Surface Registration》这篇论文将该问题转换成了近似的线性最小二乘问题，可以使用SVD求解

4.3.2算法适用范围

（1）算法比point to point 方法可以提高收敛速度，但论文中提到不一定会收敛到全局最优解

（2）算法中主要使用了法向量来计算，所以在配准中使用准确的法向量至关重要，主要可以通过两个方法来保证①对比较平滑、质量较好的点云使用该方法②如果原始点云质量不太好，那么在相对smooth区域采样，然后进行配准。

参考文献

【1】https://blog.csdn.net/pingjun5579/article/details/118546565

4.4 Plane to Plane ICP

4.4.1介绍

该方法在论文《Generalized-ICP》中最先提出来，Generalized-ICP其实是一种基于概率论的算法框架，将point to point 和point to plane作为该框架中的一种特例，并且又提出了plane to plane方法，该方法的特点是综合考虑了距离和法向量，收敛效果较好，可以纠正最大匹配距离设的值比较大的情况，具体算法介绍可以参照如下文章：

[论文阅读][ICP变种] Generalized-ICP_你代码像一首诗的博客-CSDN博客

4.4.2适用范围

由于该方法也使用了法向量，如果点云中噪声比较多，那么计算的法向量就不太准确，也会影响最终精度，对于医疗图像来说，如果骨质成像不好，直接使用移动立方体生成的stl网格是及其不平滑的，这时候可以先平滑后再使用该方法，综合icp三种方法，油管有个up主建议generalized icp应该是使用icp算法时首选的方法。

4.5 NDT算法

4.5.1原理介绍

NDT（Normal Distribution Transformation）算法主要有三篇论文：

1.  认为是它首先提出的，不过是2D

2. 领域应用到了3D

3. 做了全面的总结和拓展，博士论文

网上写该算法原理的最多是第二篇，这也是激光点云配准中经常使用的一种方法，通过学习该算法，可以知道，该算法的思想与Generalized ICP算法非常类似，都使用了概率分布，而且都假设点主要分布服从正态分布，不同的是Generalized ICP直接假设点的位置符合高斯分布，而在NDT算法中假设每个分成的小格子内部的点符合高斯概率分布（实现时会加入均匀分布），这样做我个人感觉会减少计算时间，加快计算速度。NDT基本原理和步骤如下：

（1）分成小格子，计算每个小格子中的高斯分布参数，主要是均值和协方差矩阵（协方差矩阵表征了当前小格子中点分布的平滑性和方向）

（2）通过转换矩阵T将浮动点云（moving cloud）变换到（1）中分成的小格子中，然后计算每个变换点在小格子中的概率，这个概率是该变换点在周围邻近小格子中概率之和，最后通过最大似然估计原理，将每个变换点的概率相乘得到最终的目标函数。

（3）使用牛顿迭代法求解变换矩阵，查看是否满足收敛条件，不满足，则转到（2）中。

4.5.2适用范围

这种方法相对于icp等算法，具有更好的鲁棒性，但也会受到初始条件的影响，主要通过计算概率分布作为主要的收敛目标，其应该能达到较好的形状匹配，可用于精确配准。

4.5.3一些质量较高的参考链接

（1）学习教程：点云匹配-正态分布变换NDT（Normal Distributions Transform）算法_哔哩哔哩_bilibili

（2）

点云 | 配准之NDT算法漫谈 - 墨天轮

（3）https://www.youtube.com/watch?v=MLpaC-ZG2RA

4.6 4PCS算法

没时间写了，有时间再写。

5.总结

通过这个项目，把点云配准中几个具有代表性的算法进行了梳理，小有收获。
 

6.其他参考文献：

[1] Lorensen, W. E. and H. E. Cline(1987). “Marching cubes: A high resolution 3D surface construction algorithm.” Computers & Graphics.

[2]【泡泡点云时空-PCL源码解读】PCL中的点云配准方法_算法