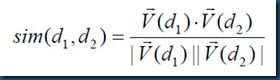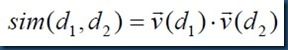信息检索导论学习笔记(8)-向量空间模型
向量空间模型
在有了tf-idf权重计算之后,一个自然的数学建模的想法是:tf-idf权重矩阵
向量空间模型
把文档看成是一个向量(vector),其中的每个分量都对应词典中的一个词项,分量值为采用tf-idf计算出的权重值。当某词项在文档中没有出现时,其对应的分量值为0。
于是,我们有一个|V|维实值空间,空间的每一维都对应词项(V为词项数目)。
对于Web搜索引擎,空间可能会上千万维。但对每个向量来说又非常稀疏(稀疏矩阵),大部分都是0。
有了向量空间模型后,那么如何对查询进行评分呢?
关键思想:将查询也看成一篇极短的文档来处理,即将查询表示成同一高维空间的向量。因此,可以通过计算给定的查询向量和每个文档向量的相似度来对所有文档进行排名。
于是评分问题转变为:在向量空间下, 如何对两篇文档的相似度进行计算?
差向量
一种自然的想法是首先考虑采用两个文档向量差向量的大小(即欧式距离)进行计算。但是这种计算方法有一个缺点:两篇内容相似的文档向量的差向量可能很大,这是因为一篇文档可能比另一篇文档要长得多。
采用夹角而不是距离来计算
根据两个文档向量的夹角大小来计算相似度。假想实验:将文档d 复制一份加在自身末尾得到文档d′,则d′ 是d的两倍。很显然,从语义上看,d 和d′具有相同的内容,代表它们之间具有最大的相似度,而两者之间的夹角为0,但是,它们的欧氏距离可能会很大。
单位向量内积
为了弥补文档长度给上述相似度计算所带来的负面效果, 计算两篇文档 d1和 d2相似度的常规方法是计算两文档向量的余弦相似度(cosine similarity):
公式中除以分母的效果实际上相当于将向量进行长度归一化(称为欧氏归一化),得到单位向量。因此公式可以重写为:
实例计算过程:
1.列出tf-idf权重矩阵
2.长度归一化
SAS文档的affection词项归一化处理:115*115/(115*115+10*10+2*2)=0.99219,开根号结果为0.996
3.列出归一化处理后的权重矩阵
则文档SAS和PAP的余弦相似度 sim(SAS,PAP)=0.996*0.993+0.087*0.12=0.999468
余弦相似度的问题
余弦归一化倾向于短文档,即对短文档产生的归一化因子太大,而平均而言对长文档产生的归一化因子太小。特别是对那些包含多个不同主题的文档,而查询词项可能只能和文档的部分内容相匹配。这时文档中词项的相对权重,就会和一篇与查询相匹配的短文档迥然不同。
于是我们要找到一种方法:对短文档的相似度降低,而长文档的相似度增大,去除原来余弦归一化偏向短文档的问题。
Amit Singhal的著名论文Pivoted Document Length Normalization提出了一种回转归一化的处理方法。
论文地址:http://ir.iit.edu/~dagr/cs529/files/handouts/singhal96pivoted.pdf
向量空间模型小结
- 将查询表示成tf‐idf权重向量
- 将每篇文档表示成同一空间下的tf‐idf权重向量
- 计算两个向量之间的某种相似度(如余弦相似度)
- 按照相似度大小将文档排序
- 将前K(如K =10)篇文档返回给用户