matlab遗传算法求解TSP旅行商问题
一、引言
本文将用matlab编写遗传算法求解TSP旅行商问题,其实是对viafcccy原文章以及《MATLAB智能算法》中基于遗传算法TSP问题复现。但是原文中有一些细节,对像我这样的小白还是有些难度,因此在这里进行重新整理,这里也给出原文链接。
1.1问题描述
旅行商问题(traveling saleman problem, TSP)又被称为推销员问题、货郎担问题,该问题是最基本的路线问题。该问题寻求单一旅行者由起点出发,通过所有给定的需求点之后,最后再回到起点的最小路径成本,路径的限制是每个需求点只能拜访一次。最早的旅行商问题的数学模型是由Dantzig(1959)等学者提出的。旅行商问题是车辆路径问题(VRP)的特例,已证明旅行商问题是NP难问题。
1.2算法实现
1.2.1个体编码
遗传算法中种群个体编码采用正数编码的方式,每个个体表示历经的需求点路线,例如,当总的需求点数量为10,个体的编码可能为[2 3 9 4 8 7 5 6 1 10],表示旅行商从需求点2开始,经过3,9,4,...最终返回需求点2,从而完成TSP遍历。
1.2.2适应度值
种群个体的适应度值表示为遍历路径的长度,计算公式为
其中,n为城市数量;![]() 为城市i,j之间的距离。
为城市i,j之间的距离。
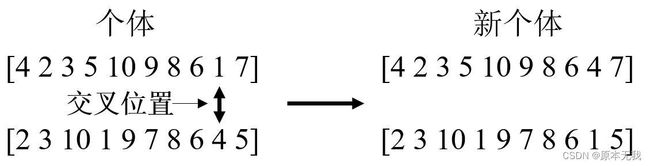
1.2.3交叉操作(算法核心之一)
个体之间通过交叉进行更新,交叉方法采用整数交叉法。首先选择两个交叉位置,然后把交叉位置进行互换。此时,产生的两个新个体很有可能存在重复的需求点位置,因此需要进行调整:
此时交叉后得到的新个体存在重复位置,调整方法为用个体汇总为涵盖的位置代替重复的位置:
1.2.4变异操作(算法核心之二)
TSP问题中为了保证个体变异后,路径仍然满足遍历所有位置,因此采用个体内部两位置互换方法,首先随机选择变异位置pos1和pos2,然后把两个变异位置互换,假设选择的变异位置为9和10,则变异后的新个体为:
对得到的新个体采用保留优秀个体策略,只有当新个体适应度比原来个体好时才进行个体变异。
二、算法实现
2.1城市位置数据
可用如下代码随机生成20个位置数据:
city_location = zeros(20,2);
city_location(:,1) = 100 * rand(20,1);
city_location(:,2) = 100 * rand(20,1);得到的位置数据如下:
15.7613081677548 70.6046088019609
97.0592781760616 3.18328463774207
95.7166948242946 27.6922984960890
48.5375648722841 4.61713906311539
80.0280468888800 9.71317812358475
14.1886338627215 82.3457828327293
42.1761282626275 69.4828622975817
91.5735525189067 31.7099480060861
79.2207329559554 95.0222048838355
95.9492426392903 3.44460805029088
65.5740699156587 43.8744359656398
3.57116785741896 38.1558457093008
84.9129305868777 76.5516788149002
93.3993247757551 79.5199901137063
67.8735154857774 18.6872604554379
75.7740130578333 48.9764395788231
74.3132468124916 44.5586200710900
39.2227019534168 64.6313010111265
65.5477890177557 70.9364830858073
17.1186687811562 75.4686681982361紧接着我们对城市坐标数据进行可视化:
clc
clear
load("city_location.mat"); % 加在数据
location = load("city_location.mat"); % 开始对数据进行可视化
x = location.city_location(:,1);
y = location.city_location(:,2);
plot(x,y,'o');
xlabel('城市横坐标');
ylabel('城市纵坐标');
grid on;计算城市之间的距离:
function D = Distance(a)
%计算两两城市之间的距离
%输入的数据为所有城市的x、y坐标位置矩阵city_location,输出为两两城市的距离构成的矩阵D
row = size(a,1);
D = zeros(row,row);
for i = 1:row
for j = i+1:row
D(i,j) = ((a(i,1)-a(j,1))^2+(a(i,2)-a(j,2))^2)^0.5;
D(j,i) = D(i,j);
end
end2.2遗传算法初始化
遗传算法相关参数设置:
NIND = 100; %种群大小
MAXGEN = 500; %最大迭代次数
Pc = 0.9; %交叉概率,相当于基因遗传的时候染色体交叉
Pm = 0.05; %染色体变异
GGAP = 0.9; %这个是代沟,通过遗传方式得到的子代数为父代数*GGAP生成初始种群:
function Chrom = InitPop(NIND,N)
%输入:
%NIND:种群大小
%N:个体染色体长度(城市个数)
%输出:初始种群
Chrom = zeros(NIND,N); % 定义存储种群的变量
for i = 1:NIND
Chrom(i,:) = randperm(N);
end2.3旅行商路线可视化
可视化旅行商轨迹:
function DrawPath(Chrom,X)
%输入:
%待画路线
%城市的坐标位置
%输出:
%旅行商的路线
R = [Chrom(1,:) Chrom(1,1)]; %第一个随机解(个体)【Chrom(1,:)取第一行数据】,一共有n个城市,但是这里R有n+1个值,因为后面又补了一个Chrom(1,1),“是为了让路径最后再回到起点”
figure;
hold on
plot(X(:,1),X(:,2),'bo')%X(:,1),X(:,2)分别代表的X轴坐标和Y轴坐标
%plot(X(:,1),X(:,2),'o','color',[1,1,1])%X(:,1),X(:,2)分别代表的X轴坐标和Y轴坐标,
plot(X(Chrom(1,1),1),X(Chrom(1,1),2),'rv','MarkerSize',20)%标记起点
A = X(R,:); %A是将之前的坐标顺序用R打乱后重新存入A中
row = size(A,1); %row为坐标数+1
for i = 2:row
[arrowx,arrowy] = dsxy2figxy(gca,A(i-1:i,1),A(i-1:i,2)); %dsxy2figxy坐标转换函数,记录两个点
annotation('textarrow',arrowx,arrowy,'HeadWidth',5,'color',[0,0,1]);%将这两个点连接起来
end
hold off
xlabel('横坐标x')
ylabel('纵坐标y')
title('旅行商轨迹图')
box on注意这个函数中的dsxy2figxy函数是必须存在的,因为annotation函数中两个点的坐标必须转化在0,1之间
function varargout = dsxy2figxy(varargin) %%将两点坐标值转化至0,1之间
if length(varargin{1}) == 1 && ishandle(varargin{1}) ...
&& strcmp(get(varargin{1},'type'),'axes')
hAx = varargin{1};
varargin = varargin(2:end);
else
hAx = gca;
end
if length(varargin) == 1
pos = varargin{1};
else
[x,y] = deal(varargin{:});
end
axun = get(hAx,'Units');
set(hAx,'Units','normalized');
axpos = get(hAx,'Position');
axlim = axis(hAx);
axwidth = diff(axlim(1:2));
axheight = diff(axlim(3:4));
if exist('x','var')
varargout{1} = (x - axlim(1)) * axpos(3) / axwidth + axpos(1);
varargout{2} = (y - axlim(3)) * axpos(4) / axheight + axpos(2);
else
pos(1) = (pos(1) - axlim(1)) / axwidth * axpos(3) + axpos(1);
pos(2) = (pos(2) - axlim(3)) / axheight * axpos(4) + axpos(2);
pos(3) = pos(3) * axpos(3) / axwidth;
pos(4) = pos(4) * axpos(4 )/ axheight;
varargout{1} = pos;
end
set(hAx,'Units',axun)编写函数将最优路径输出
function p=OutputPath(R)
%打印路线函数
%以1->2->3的形式在命令行打印路线
R = [R,R(1)];
N = length(R);
p = num2str(R(1));
for i = 2:N
p = [p,'->',num2str(R(i))];
end
disp(p)2.4目标函数及适应度函数
目标函数为个体经历的路径总和
function len = PathLength(D,Chrom)
%计算所有个体的路线长度
%输入
%D两两城市之间的距离
%Chrom个体的轨迹
[~,col] = size(D); %返回D的列数
NIND = size(Chrom,1);%NIND等于初始种群
len = zeros(NIND,1);%初始化一个大小等于NIND的len来记录长度
for i = 1:NIND
p = [Chrom(i,:) Chrom(i,1)];%构造p矩阵保存路线图 将第一行路线提出 再加上第一个构成回路
i1 = p(1:end-1);%i1从第一个开始遍历到倒数第二个
i2 = p(2:end);%i2从第二个开始遍历到倒数第一个
len(i,1) = sum(D((i1-1)*col+i2));%计算出每种路线(种群的个体)的长度,这里相当于把D矩阵沿行展开
end计算个体的适应度,适应度用于评价个体的优劣程度,适应度越大个体越好,反之适应度越小则个体越差,这里将目标值的倒数作为适应度:
function FitnV = Fintness(len) %适应度函数
%输入:
%len 个体的长度(TSP的距离)
%输出:
%FitnV 个体的适应度值
FitnV = 1./len;2.5选择、交叉、变异、重插入
2.5.1选择
这里直接采用原文的方式,尝试编写了轮盘赌代码,失败了。。
function NewChrIx = Sus(FitnV,Nsel)
%输入:
%FitnV 个体的是适应度值
%Nsel 被选个体的数目
%输出:
%NewChrIx 被选择个体的索引号
[Nind,ans] = size(FitnV);%Nind为FitnV的行数也就是个体数 ans为列数1
cumfit = cumsum(FitnV);%对适应度累加 例如 1 2 3 累加后 1 3 6 用来计算累积概率
trials = cumfit(Nind)/Nsel * (rand + (0:Nsel-1)');%cumfit(Nind)表示的是矩阵cumfit的第Nind个元素 A.'是一般转置,A'是共轭转置 rand返回一个在区间 (0,1) 内均匀分布的随机数
%cumfit(Nind)/Nsel平均适应度 * (rand +(0:Nsel-1)')从0开始到89的转置矩阵(行矩阵变列矩阵)加上每一项加上一个0-1的随机数
%生成随机数矩阵 用来筛选
Mf = cumfit(:,ones(1,Nsel));%将生成的累积概率 复制90份 生成一个100*90的矩阵
Mt = trials(:,ones(1,Nind))';
[NewChrIx,ans] = find(Mt编写Select函数
function SelCh = Select(Chrom,FitnV,GGAP)
%输入:
%Chrom 种群
%FitnV 适应度值
%GGAP 选择概率
%输出:
%SelCh 被选择的个体
NIND = size(Chrom,1);%种群个体总数
NSel = max(floor(NIND * GGAP+.5),2);%确定下一代种群的个体数,如果不足二个就计为二个
ChrIx = Sus(FitnV,NSel);
SelCh = Chrom(ChrIx,:);2.5.2 交叉
交叉分为两部分,首先是两个个体之间的交叉规则,要保证每个个体遍历需求点:
function [a,b] = intercross(a,b)
%输入:
%a和b为两个待交叉的个体
%输出:
%a和b为交叉后得到的两个个体
L = length(a);
%随机产生交叉区段
r1 = randsrc(1,1,[1:L]); % 这里先随机选出两个位置,位置不能超过
r2 = randsrc(1,1,[1:L]); %
if r1~=r2
a0 = a;
b0 = b;
s = min([r1,r2]);
e = max([r1,r2]);
for i = s:e
a1 = a;
b1 = b;
%第一次互换
a(i) = b0(i);
b(i) = a0(i);
%寻找相同的城市
x = find(a==a(i)); % 如果有相同的城市,x会得到包含i的两个值,y同理
y = find(b==b(i));
%第二次互换产生新的解
i1 = x(x~=i); % 将位置不是i但相同的城市标记出来
i2 = y(y~=i);
if ~isempty(i1)
a(i1)=a1(i);
end
if ~isempty(i2)
b(i2)=b1(i); % 注意,原文这里有误,应该是b(i2)
end
end
end
% 这里增加一段代码,r1=r2时,两个个体只在一点交叉
if r1 == r2
a0 = a;
b0 = b;
a(r1) = b0(r1);
b(r1) = a0(r1);
x = find(a==a(r1));
y = find(b==b(r1));
i1 = x(x~=r1);
i2 = y(y~=r1);
if ~isempty(i1)
a(i1) = a0(r1);
end
if ~isempty(i2)
b(i2) = b0(r1);
end
end
其次是总的交叉函数
function SelCh = Recombin(SelCh,Pc)
%交叉操作
%输入:
%SelCh 被选择的个体
%Pc 交叉概率
%输出:
%SelCh 交叉后的个体
NSel = size(SelCh,1);
for i = 1:2:NSel - mod(NSel,2) % 若不减去余数且NSel如果是奇数,最后一个i会等于NSel,i+1报错
if Pc>=rand %交叉概率PC
[SelCh(i,:),SelCh(i+1,:)] = intercross(SelCh(i,:),SelCh(i+1,:));
end
end2.5.3 变异
这里选择了一种较为简单的变异方式,去掉了原文逆转的过程,即保证变异后的个体的目标值减小,否则不进行变异:
function SelCh = Mutate(SelCh,D,Pm)
%变异操作
%输入:
%SelCh 被选择的个体
%Pm 变异概率
%输出:
%SelCh 变异后的个体
index = SelCh;
col = size(SelCh,2); %返回SelCh的列数
%lenSelCh = [];
lenSelCh = PathLength(D,SelCh);
[NSel,L] = size(SelCh);
for i = 1:NSel
if Pm >= rand
R = randperm(L);
index(i,R(1:2)) = index(i,R(2:-1:1)); % 将个体i中R(1)和R(2)这两个位置的城市互换
p = [index(i,:) index(i,1)];
i1 = p(1:end-1);
i2 = p(2:end);
DIndexi = sum(D((i1-1)*col+i2)); % 计算出变异后个体的路径距离
if DIndexi < lenSelCh(i) % 如果变异后路径距离比变异前更小,则保留变异
SelCh(i) = index(i);
end
end
end2.5.4重插入
function Chrom = Reins(Chrom,SelCh,ObjV)
%重插入子代的种群
%输入:
%Chrom 父代的种群
%SelCh 子代的种群
%ObjV 父代适应度
%输出:
%Chrom 组合父代与子代后得到的新种群
NIND = size(Chrom,1);
NSel = size(SelCh,1);
[TobjV,index] = sort(ObjV);
Chrom = [Chrom(index(1:NIND-NSel),:);SelCh];三、主函数及结果
重新编写了图形输出代码,主函数如下
clc
clear
load("city_location.mat"); % 加在数据
location = load("city_location.mat"); % 开始对数据进行可视化
x = location.city_location(:,1);
y = location.city_location(:,2);
plot(x,y,'o');
xlabel('城市横坐标');
ylabel('城市纵坐标');
%grid on;
NIND = 100; %种群大小
MAXGEN = 100; %最大迭代次数
Pc = 0.9; %交叉概率,相当于基因遗传的时候染色体交叉
Pm = 0.05; %染色体变异
GGAP = 0.9; %这个是代沟,通过遗传方式得到的子代数为父代数*GGAP
D = Distance(city_location); %通过这个函数可以计算i,j两点之间的距离
N = size(D,1); %计算有多少个坐标点
%%初始化种群
Chrom = InitPop(NIND,N); %Chrome代表的种群
%%画出随机解得路线图
DrawPath(Chrom(1,:),city_location)
pause(0.0001)
%输出随机解的路线和总距离
disp('初始种群中的一个随机值')
OutputPath(Chrom(1,:));%其中一个个体
Rlength = PathLength(D,Chrom(1,:));
disp(['总距离;',num2str(Rlength)]);
disp('~~~~~~~~~~~~~~~~~~~~~~~~~~~~~')
%优化
gen = 0;
trace = zeros(1,MAXGEN);
title('优化过程')
xlabel('迭代次数')
ylabel('当前最优解')
ObjV = PathLength(D,Chrom);%计算当前路线长度,即上面随机产生的那些个体路径
preObjV = min(ObjV);%当前最优解
while gen所得结果如下:
这里需要注意的是,用简化的变异代码求解后,最优解基本在400以上,下面加入逆转算法对模型进行求解。
四、选择、交叉、变异后的逆转
逆转算法的主要思想为,在一个个体中的路径中随机选择两个位置,对中间的城市进行逆转,若逆转后的路径和变小,则保留逆转后的个体,否则不保留。
function SelCh = Reverse(SelCh,D)
%进化逆转函数
%输入:
%SelCh 被选择的个体
%D 各城市的距离矩阵
%输出:
%SelCh 进化逆转后的个体
[row,col] = size(SelCh);
ObjV = PathLength(D,SelCh);
SelCh1 = SelCh;
for i = 1:row
r1 = randsrc(1,1,[1:col]);
r2 = randsrc(1,1,[1:col]);
mininverse = min([r1 r2]);
maxinverse = max([r1 r2]);
SelCh1(i,mininverse:maxinverse) = SelCh1(i,maxinverse:-1:mininverse);
end
ObjV1 = PathLength(D,SelCh1);%计算路线长度
index = ObjV1结果如下:
最优解:
11->17->8->3->2->10->5->15->4->12->1->20->6->18->7->19->9->14->13->16->11
旅行商走过的总距离:379.0725经过多次实验发现,加入逆转过程后,遗传算法的效果明显得到提升。至此,代码已全部完成。
虽然代码复现完成,但是结果有时还是会出现bug,主要存在于得到的最优解中,有时会有一个城市被忽略,不知道问题出在哪里,欢迎大家检验指出。
参考链接
matlab遗传算法(GA)详解(二)旅行商问题(TSP)详解_viafcccy的博客-CSDN博客_旅行商问题matlab算法
《MATLAB智能算法30个案例分析(第二版)》