PCL中3D点云特征描述与提取（二）

1 点特征直方图描述子

  正如点特征表示法所示，表面法线和曲率估计是某个点周围的几何特征基本表示法。虽然计算非常快速容易，但是无法获得太多信息，因为它们只使用很少的几个参数值来近似表示一个点的k邻域的几何特征。然而大部分场景中包含许多特征点，这些特征点有相同的或者非常相近的特征值，因此采用点特征表示法，其直接结果就减少了全局的特征信息。本小节将介绍三维特征描述子中的一位成员：点特征直方图（Point Feature Histograms），我们简称为PFH，本小节将介绍它的理论优势，从PCL实现的角度讨论其实施细节。PFH特征不仅与坐标轴三维数据有关，同时还与表面法线有关。

1.1 理论基础

  PFH计算方式通过参数化查询点与邻域点之间的空间差异，并形成一个多维直方图对点的k邻域几何属性进行描述。直方图所在的高维超空间为特征表示提供了一个可度量的信息空间，对点云对应曲面的6维姿态来说它具有不变性，并且在不同的采样密度或邻域的噪声等级下具有鲁棒性。点特征直方图（PFH）表示法是基于点与其k邻域之间的关系以及它们的估计法线，简言之，它考虑估计法线方向之间所有的相互作用，试图捕获最好的样本表面变化情况，以描述样本的几何特征。因此，合成特征超空间取决于每个点的表面法线估计的质量。下图表示的是一个查询点（$P_q$）的PFH计算的影响区域，$P_q$用红色标注并放在圆球的中间位置，半径为r，$P_q$的所有k邻元素（即与点$P_q$的距离小于半径r的所有点）全部互相连接在一个网络中，最终的PFH描述子通过计算邻域内所有两点之间关系而得到的直方图，因此存在一个O(K)的计算复杂性。

查询点（$P_q$）的PFH计算的影响区域

  为了计算两点 $P_i$ 和 $P_j$ 及与它们对应的法线 $n_i$ 和 $n_j$ 之间的相对偏差，在其中的一个点上定义一个固定的局部坐标系，如下图所示：

定义一个固定的局部坐标系

  使用上图中uvw坐标系，法线 $n_s$ 和 $n_t$ 之间的偏差可以用一组角度来表示，如下所示：
$$u=n_s$$
$$v=u\times \frac{\left(P_t-P_s\right)}{{\Vert P_t-P_s\Vert }_2}$$
$$w=u\times v$$
$$\alpha =v\cdot n_t$$
$$\varphi =u\cdot \frac{\left(P_t-P_s\right)}{d}$$
$$\theta =arctan\left(w\cdot n_t,u\cdot n_t\right)$$

  $d$ 是两点 $P_s$ 和 $P_t$ 之间的欧氏距离，$d={\Vert P_t-P_s\Vert }_2$。计算k邻域内的每一对点的$<\alpha ,\varphi ,\theta ,d>$四组值，这样就把两点和它们法线相关的12个参数（$xyz$坐标值和法线信息）减少到4个。

  为每一对点估计PFH四元组，可以使用如下代码：

pcl::computePairFeatures (const Eigen::Vector4f &  	p1,
						  const Eigen::Vector4f &  	n1,
						  const Eigen::Vector4f &  	p2,
					      const Eigen::Vector4f &  	n2,
						  float &  	f1,
						  float &  	f2,
						  float &  	f3,
						  float &  	f4 
)

  有关其他详细信息，请见API文件。为查询点创建最终的PFH表示，所有的四元组将会以某种统计的方式放进直方图中，这个过程首先把每个特征值范围划分为b个子区间，并统计落在每个子区间的点数目，因为四分之三的特征在上述中为法线之间的角度计量，在三角化圆上可以将它们的参数值非常容易地归一到相同的区间内。一个统计的例子是：把每个特征区间划分成等分的相同数目，为此在一个完全关联的空间内创建有 $b^4$ 个区间的直方图。在这个空间中，每计算一个点对的四个特征值，直方图中对于该点对的四个特征值特定区间的统计个数加1。如下图所示，就是点云中不同点的点特征直方图表示法的一个例子，在某些情况下，第四个特征量 $d$ 在通常由机器人捕获的2.5维数据集中并不重要，因为邻近点间的距离从视点开始是递增的，而并非不变的，在扫描中局部点密度影响特征时，实践证明省略 $d$ 是有益的。

点云中不同点的点特征直方图表示法

  注意：更多相关信息和数学推导，包括不同几何体表面点云的PFH特征分析，请见该文章。

1.2 估计PFH特征

  点特征直方图（PFH）在PCL中的实现是 pcl_features 模块的一部分。默认PFH的实现
使用5个区间分类（例如：四个特征值中的每个都使用5个区间来统计），其中不包括距离（在上文中已经解释过了——但是如果有需要的话，也可以通过用户调用 computePairFeatures 方法来获得距离值），这样就组成了一个125浮点数元素的特征向量（$3^5$），其保存在一个 pcl::PFHSignature125 的点类型中。以下代码段将对输入数据集中的所有点估计其对应的PFH特征。

#include         // 点类型头文件
#include        // PFH特征估计类头文件

{
    pcl::PointCloud<pcl::PointXYZ>::Ptr cloud (new pcl::PointCloud<pcl::PointXYZ>);
    pcl::PointCloud<pcl::Normal>::Ptr normals (new pcl::PointCloud<pcl::Normal> ());

    ... 打开原始点云数据，计算法线 ...
    
    /* 创建PFH估计对象pfh，并将输入点云数据集cloud和法线normals传递给它 */
    pcl::PFHEstimation<pcl::PointXYZ, pcl::Normal, pcl::PFHSignature125> pfh;
    pfh.setInputCloud (cloud);
    pfh.setInputNormals (normals);
    // 如果点云类型为 PointNormal，则执行 pfh.setInputNormals (cloud);

    // 创建一个空的kd树表示法，并把它传递给PFH估计对象
    // 基于已给的输入数据集，建立kdtree
    pcl::search::KdTree<pcl::PointXYZ>::Ptr tree (new pcl::search::KdTree<pcl::PointXYZ> ());
    pfh.setSearchMethod (tree);

    // 输出数据集
    pcl::PointCloud<pcl::PFHSignature125>::Ptr pfhs (new pcl::PointCloud<pcl::PFHSignature125> ());

    // 使用半径在5cm范围内的所有邻元素
    // 注意，此处使用的半径必须大于估计表面法线时使用的半径
    pfh.setRadiusSearch (0.05);

    // 计算PFH特征值
    pfh.compute (*pfhs);

    // pfh->size () 应该与 cloud->size ()有相同的大小，即每个点都有一个PFH特征向量
}

  PFHEstimation 类的实际计算程序内部只执行以下操作：
  对点云 $P$ 中的每个点 $p$：
  （1）得到 $p$ 点的最近邻元素；
  （2）对于邻域内的每对点，计算其三个角度特征参数值；
  （3）将所有结果统计到一个输出直方图中。

  使用下列代码，从一个k邻域计算单一的PFH描述子。

computePointPFHSignature (const pcl::PointCloud<PointInT> &cloud,
                          const pcl::PointCloud<PointNT> &normals,
                          const std::vector<int> &indices,
                          int nr_split,
                          Eigen::VectorXf &pfh_histogram);

  此处，cloud变量是包含点的输入点云，normals变量是包含对应 cloud 的法线的输入点云，indices 代表输入点云（点与法线对应）中查询点的k近邻元素集，nr_split是所分区间的数目，用于每个特征区间的统计过程， pfh_histogram是浮点数向量用来存储输出的合成直方图。

2 快速点特征直方图描述子

  已知点云 $P$ 中有 $n$ 个点，那么它的点特征直方图（PFH）的理论计算复杂度是 $O(n{k}^2)$ ，其中 $k$ 是点云 $P$ 中每个点 $p$ 计算特征向量时考虑的邻域数量。对于实时应用或接近实时应用中，密集点云的点特征直方图（PFH）的计算，是一个主要的性能瓶颈。本小节讲述PFH计算方式的简化形式，我们称为快速点特征直方图FPFH（Fast Point Feature Histograms）（更多详情查看相关文献），FPFH把算法的计算复杂度降低到了 $O(nk)$，但是仍然保留了PFH大部分的识别特性。

2.1 理论基础

  为了简化直方图的特征计算，我们执行以下过程。

  第一步，对于每一个查询点 $P$，计算这个点和它的邻域点之间的一个元组$<\alpha ,\varphi ,\theta >$（参考上一节PFH的介绍），第一步结果我们称之为简化的点特征直方图SPFH（Simple Point Feature Histograms）；

  第二步，重新确定每个点的 $k$ 邻域，使用邻近的SPFH来计算 $P_q$ 的最终直方图（称为FPFH），如下所示：
$$FPFH\left(P_q\right)=SPFH\left(P_q\right)+\frac{1}{k}\sum _{i=1}^k\frac{1}{w_k}\cdot SPFH\left(P_k\right)$$

  上式中，权重 $w_k$ 在一些给定的度量空间中，表示查询点 $P_q$ 和其邻近点 $P_k$ 之间的距离，因此可用来评定一对点（$P_q，P_k$），但是如果需要的话，也可以用 $w_k$ 的另一种度量来表示，如下图所示，它表示的是以点 $P_q$ 为中心的k邻域影响范围。

以点 $P_q$ 为中心的k邻域影响范围图

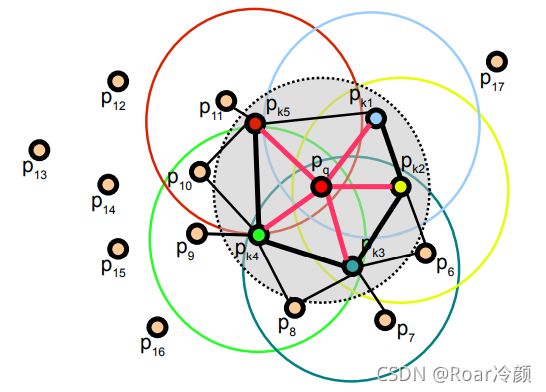
  因此，对于一个已知查询点 $P_q$ ，这个算法首先只利用 $P_q$ 和它邻域点之间对应点对（以上图中红色线来说明），来估计它的SPFH值，很明显这样比PFH的标准计算少了邻域点之间的互联。点云数据集中的所有点都要执行这一计算获取SPFH，接下来使用它的邻近点$P_k$的SPFH值和$P_q$点的SPFH值重新权重计算，从而得到$P_q$点的最终FPFH值。FPFH计算添加的计算连接对，在上图中以黑色线表示。如上图所示，一些重要对点（与$P_q$直接相连的点）被重复计数两次（图中以粗线来表示），而其他间接相连的用细黑线表示。

2.2 PFH和FPFH的区别

  PFH和FPFH计算方式之间的主要区别总结如下。
  （1）FPFH没有对全互联$P_q$点的所有邻近点的计算参数进行统计，因此可能漏掉了一些重要的点对，而这些漏掉的点对可能对捕获查询点周围的几何特征有贡献；
  （2）PFH特征模型是在查询点周围的一个精确的邻域半径内，而FPFH还包括半径r范以外的额外点对（不过在2r内）；
  （3）因为重新权重计算的方式，所以FPFH结合SPFH值，重新捕获邻近重要点对的几何信息；
  （4）由于大大地降低了FPFH的整体复杂性，因此FPFH有可能使用在实时应用中；
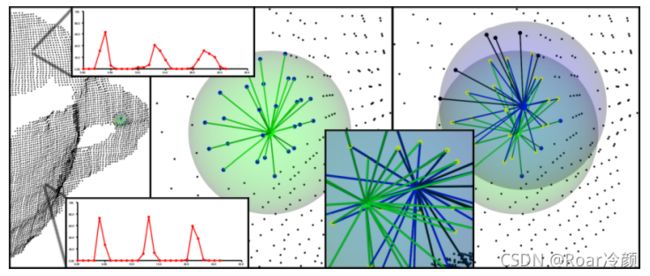
  （5）通过分解三元组，简化了合成的直方图。也就是简单生成d分离特征直方图，对每个特征维度来单独绘制，并把它们连接在一起，如下图所示。

PFH和FPFH示意图

2.3 估计FPFH特征

  快速点特征直方图FPFH在点云库中的实现可作为pcl_features库的一部分。默认的FPFH实现使用11个统计子区间（例如：四个特征值中的每个都将它的参数区间分割为11个），特征直方图被分别计算然后合并得出了浮点值的一个33元素的特征向量，这些保存在一个pcl::PFHSignature33点类型中。以下代码段将对输入数据集中的所有点估计一组FPFH特征值。

#include 
#include   // FPFH特征估计类头文件声明

{
    pcl::PointCloud<pcl::PointXYZ>::Ptr cloud (new pcl::PointCloud<pcl::PointXYZ>);
    pcl::PointCloud<pcl::Normal>::Ptr normals (new pcl::PointCloud<pcl::Normal> ());

    ... 打开原始点云数据，计算法线 ...
    
    /* 创建FPFH估计对象fpfh，并将输入点云数据集cloud和法线normals传递给它 */
    pcl::FPFHEstimation<pcl::PointXYZ, pcl::Normal, pcl::FPFHSignature33> fpfh;
    fpfh.setInputCloud (cloud);
    fpfh.setInputNormals (normals);
    // 如果点云类型为 PointNormal，则执行 fpfh.setInputNormals (cloud);

    // 创建一个空的kd树表示法，并把它传递给FPFH估计对象
    // 基于已给的输入数据集，建立kdtree
    pcl::search::KdTree<PointXYZ>::Ptr tree (new pcl::search::KdTree<PointXYZ>);

    fpfh.setSearchMethod (tree);

    // 输出数据集
    pcl::PointCloud<pcl::FPFHSignature33>::Ptr fpfhs (new pcl::PointCloud<pcl::FPFHSignature33> ());

    // 使用半径在5cm范围内的所有邻元素
    // 注意，此处使用的半径必须大于估计表面法线时使用的半径
    fpfh.setRadiusSearch (0.05);

    // 计算FPFH特征向量
    fpfh.compute (*fpfhs);

    // fpfhs->size () 应该和 cloud->size ()有相同的大小，即每个点都有一个FPFH特征向量
}

  FPFHEstimation 类的实际计算程序内部只执行以下操作：
  对点云 $P$ 中的每个点 $p$：
  第一步：
  （1）得到 $p$ 点的邻域元素；
  （2）计算每一对（$p，p_k$）的三个角度参数值（其中 $p_k$ 是 $p$ 的邻元素）；
  （3）把所有结果统计输出到一个SPFH直方图；
  第二步：
  （1）得到 $p$ 点的最近邻元素；
  （2）使用 $p$ 的每一个SPFH和一个权重计算式，来计算点 $p$ 最终的FPFH。

2.4 使用OpenMP提高FPFH速度

  对于计算速度要求苛刻的用户，PCL提供了一个FPFH估计的另一实现，它使用多核/多线程规范，利用OpenMP开发模式来提高计算速度，这个类的名称是 pcl::FPFHEstimationOMP，并且它的应用程序接口(API)100%兼容单线程pcl::FPFHEstimation，这使它适合作为一个替换元件，在8核系统中，OpenMP的实现可以在6~8倍更快的计算时间内完全同样单核系统上的计算。

3 估计一点云的VFH特征

  本小节介绍视点特征直方图（Viewpoint Feature Histogram）描述子，它是一种新的表示形式，应用在点云聚类识别和六自由度位姿估计问题，下图展示了VFH识别和位姿估计的一个例子。已知一组训练样本数据（除最左端的点云之外的首行、底行）,学习了一个模型，然后使用一个点云（左下方）来查询/测试这个模型。从左下方开始，匹配结果从左到右是按照最好到最坏的顺序排列的。

VFH识别和位姿估计示意图

3.1 理论基础

  视点特征直方图（VFH）是源于FPFH描述子。由于它的获取速度和识别力，我们决定利用FPFH强大的识别力，但是为了使构造的特征保持缩放不变性的性质同时，还要区分不同的位姿，计算时需要考虑加入视点变量。我们做了以下两种计算来构造特征，以应用于目标识别问题和位姿估计：（1）扩展FPFH，使其利用整个点云对象来进行计算估计（如下图所示），在计算FPFH时以物体中心点与物体表面其他所有点之间的点对作为计算单元；（2）添加视点方向与每个点估计法线之间额外的统计信息，为了达到这个目的，关键思路是在FPFH计算中将视点方向变量直接融入相对法线角计算当中。

扩展的FPFH分量计算示意图

  通过统计视点方向与每个法线之间角度的直方图来计算视点相关的特征分量。注意：并不是每条法线的视角，因为法线的视角在尺度变换下具有可变性，这里指的是平移视点到查询点后的视点方向和每条法线间的角度。第二组特征分量就是前面PFH中讲述的三个角度，如PFH小节所述，只是现在测量的是在中心点的视点方向和每条表面法线之间的角度，如下图所示：

视点方向与法线之间分量计算示意图

  因此新组合的特征被称为视点特征直方图（VFH）。下图体现的就是新特征的想法，包含了以下两部分：
  （1）一个视点方向相关的分量；
  （2）一个包含扩展FPFH的描述表面形状的分量。

VFH直方图

3.2 估计VFH特征值

  视点特征直方图在PCL中的实现属于pcl_features模块库的一部分。对扩展的FPFH分量来说，默认的VFH的实现使用45个子区间进行统计，而对于视点分量要使用128个子区间进行统计，这样VFH就由一共308个浮点数组成阵列。在PCL中利用pcl::VFHSignature308的点类型来存储示，PFH/FPFH描述子和VFH之间的主要区别是：对于一个已知的点云数据集，只对应一个单一的VFH描述子，而合成的PFH/FPFH特征的数目和点云中的点数目相同。以下代码段将对输入数据集中的所有点估计一组VFH特征值。

#include 
#include    // VFH特征估计类头文件

{
    pcl::PointCloud<pcl::PointXYZ>::Ptr cloud (new pcl::PointCloud<pcl::PointXYZ>);
    pcl::PointCloud<pcl::Normal>::Ptr normals (new pcl::PointCloud<pcl::Normal> ());

    ... 打开原始点云数据，计算法线 ...
    
    /* 创建VFH估计对象vfh，并将输入点云数据集cloud和法线normals传递给它 */
    pcl::VFHEstimation<pcl::PointXYZ, pcl::Normal, pcl::VFHSignature308> vfh;
    vfh.setInputCloud (cloud);
    vfh.setInputNormals (normals);
    // 如果点云类型为 PointNormal，则执行 vfh.setInputNormals (cloud);

    // 创建一个空的kd树表示法，并把它传递给VFH估计对象
    // 基于已给的输入数据集，建立kdtree
    pcl::search::KdTree<pcl::PointXYZ>::Ptr tree (new pcl::search::KdTree<pcl::PointXYZ> ());
    vfh.setSearchMethod (tree);

    // 输出数据集
    pcl::PointCloud<pcl::VFHSignature308>::Ptr vfhs (new pcl::PointCloud<pcl::VFHSignature308> ());

    // 计算特征值
    vfh.compute (*vfhs);

    // vfhs->size () 的大小应该是1，即vfh描述子是针对全局的特征描述
}

3.3 可视化VFH特征

  libpcl_visualization 包含一个特殊的PCLHistogramVisualization 类，它也被 pcl_viewer 用来自动显示一个浮点值的直方图VFH描述子，对于从点云估计得到的VFH文件与pcd文件一样，也是点云文件，可视化可以同样利用pcl_viewer 点云查看工具查看，查看结果如下图所示：

VFH特征可视化