Python计算机视觉编程_03

前言

什么是全景拼接？简单来说就是将两幅或多幅具有重叠区域的图像，合并成一张大图

如图所示，7张不同的图像最后拼接成一幅大图，那么问题很明显，如何拼接呢？

1.单应性变换

如果是最简单图像拼接，很明显，我们只需要对其进行平移，将重叠区域叠加，很轻松的就能得到一幅拼接图像。但实际上两幅图像之间有很多种关系，包括但不限于平移，旋转，尺度变换，仿射，透视映射，桶状映射等等。


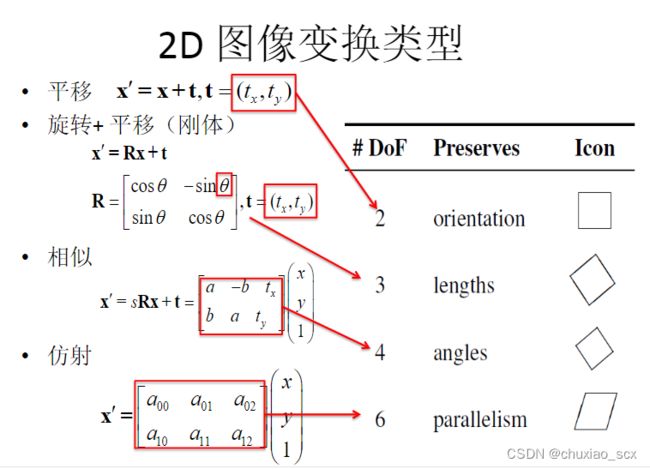
左边的图像由右边两幅图像拼接而成，很明显，右边两幅图像之间不仅有平移，还有旋转，还有拉伸等等，我们将右边的两幅图像转换成我们想要的平面图像，这个过程就是单应性变换。

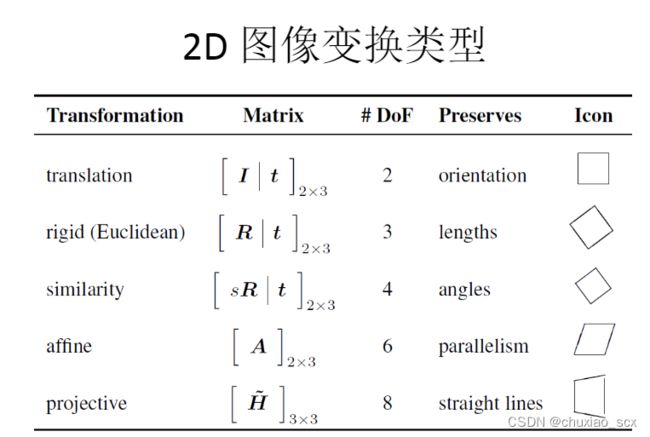
上面这个表格显示了不同变换方式所带的未知参数个数，我们以平移为例子，两幅具有平移关系的图像，我们如何拼接呢？

如图所示，两幅图像之间的映射关系如何得到呢，很明显，理论上来说如果匹配的特征点完全正确，我们只需要一个匹配对就可以得到映射关系，比如这对匹配对为（25,25）和（50,50），那么右图先与左图重叠，再将右图往左移动25像素点，然后再向下移动25个像素点，就可以将两幅图像拼接了。
当然，完全正确的匹配点一般只存在于理论当中，所以我们需要一个误差函数来判断每个映射关系的好坏，通过这个误差函数来选择最合适的映射关系。而这个误差函数采用的方法就是我们熟悉的最小二乘法。这里就不对最小二乘法展开讲了，有兴趣的可以自行百度搜索，很多大佬讲的都很清晰。
而对于单应性变换，我们有以下公式

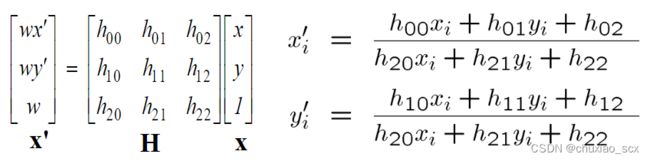
很显然，8个位置参数，我们需要4个匹配特征才能得出一种映射关系，如果将每种可能性都进行计算，所需要的资源量是非常巨大的，所以我们使用RANSAC（RAndom SAmple Consensus）算法来对其进行优化求解。

2.RANSAC算法

RANSAC解决了计算量过大的问题，通过采用缩小匹配点范围来进一步优化映射函数，流程如下
1.随机选择四对匹配特征
2.根据直接线性变换解法DLT计算单应矩阵H(唯一解)
3.对所有匹配点，计算映射误差ε=||pi’, Hpi|| ，比如A和B两幅图像融合，A的a经过H变换后为a’,与B图的对应匹配点b相减，得到对应匹配对的误差。
4.根据误差阈值，确定inliers（例如3-5像素），比如xa’-xb<5且ya’-yb<5则认为映射正确，将原来的a点加入inliers集合并令该集合统计数+1
5.针对最大inliers集合，重新计算单应矩阵H
比如我们的匹配对有一半正确和一半错误，那么一次性就能得到正确的映射关系的可能性为1/16，而实际操作中正确：错误的比例往往是10:1甚至更高，也就是说一次性得到正确的映射关系的概率为65%

3.Multi-Band Blending策略

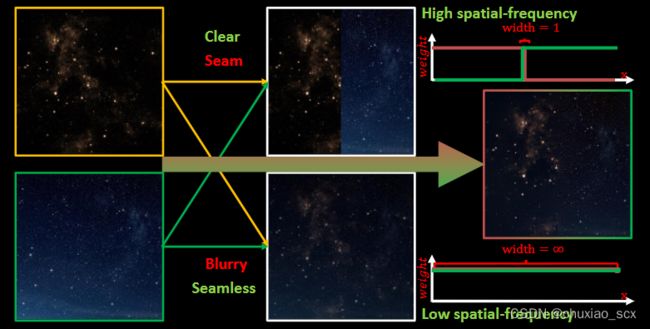
尽管可以通过RANSAC算法快速得到正确的映射策略，但在进行图像融合的时候还是可以很明显的看出不同图像之间的界限，这个界限也就是我们说的拼接缝，拼接缝的产生原因有很多，但总结起来基本上都是一个原因，光照。因为时间与空间的不同，不同图像的光照程度也不一样，从而导致拼接缝十分明显。
Multi-Band Blending的流程如下：
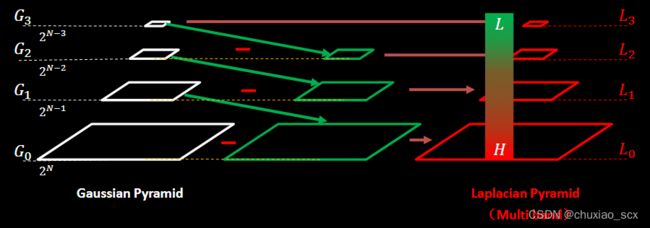
1.建立两幅图像的拉普拉斯金字塔
2.求高斯金字塔（掩模金字塔-为了拼接左右两幅图像）因为其具有尺度不变性
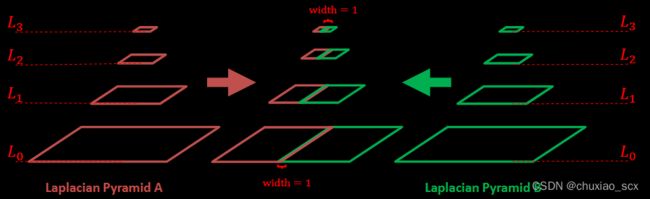
3. 进行拼接blendLapPyrs() ; 在每一层上将左右laplacian图像直接拼起来得结果金字塔resultLapPyr
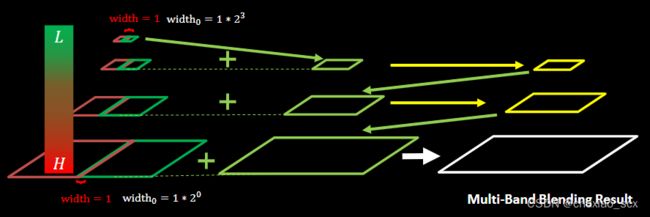
4.重建图像: 从最高层结果图
将左右laplacian图像拼成的resultLapPyr金字塔中每一层，从上到下插值放大并和下一层相加，即得blend图像结果（reconstructImgFromLapPyramid）
我们可以将拉普拉斯金字塔理解为高斯金字塔的逆形式。

4.代码实现

from pylab import *
from numpy import *
from PIL import Image

# If you have PCV installed, these imports should work
from PCV.geometry import homography, warp
from PCV.localdescriptors import sift
np.seterr(invalid='ignore')
"""
This is the panorama example from section 3.3.
"""

# 设置数据文件夹的路径
featname = ['D:\\vscode\\python\\.vscode\\jpg\\' + str(i + 1) + '.sift' for i in range(3)]
imname = ['D:\\vscode\\python\\.vscode\\jpg\\' + str(i + 1) + '.jpg' for i in range(3)]

# 使用sift算法提取特征并匹配
l = {}
d = {}
for i in range(3):
    sift.process_image(imname[i], featname[i])
    l[i], d[i] = sift.read_features_from_file(featname[i])

matches = {}
for i in range(2):
    matches[i] = sift.match(d[i + 1], d[i])

# 可视化匹配
for i in range(2):
    im1 = array(Image.open(imname[i]))
    im2 = array(Image.open(imname[i + 1]))
    figure()
    sift.plot_matches(im2, im1, l[i + 1], l[i], matches[i], show_below=True)


# 将匹配转换成齐次坐标点的函数
def convert_points(j):
    ndx = matches[j].nonzero()[0]
    fp = homography.make_homog(l[j + 1][ndx, :2].T)
    ndx2 = [int(matches[j][i]) for i in ndx]
    tp = homography.make_homog(l[j][ndx2, :2].T)

    # switch x and y - TODO this should move elsewhere
    fp = vstack([fp[1], fp[0], fp[2]])
    tp = vstack([tp[1], tp[0], tp[2]])
    return fp, tp


# 估计单应性矩阵
model = homography.RansacModel()

fp, tp = convert_points(1)
H_12 = homography.H_from_ransac(fp, tp, model)[0]  # im 1 to 2

fp, tp = convert_points(0)
H_01 = homography.H_from_ransac(fp, tp, model)[0]  # im 0 to 1

# 扭曲图像
delta = 2000  # for padding and translation用于填充和平移

im1 = array(Image.open(imname[1]), "uint8")
im2 = array(Image.open(imname[2]), "uint8")
im_12 = warp.panorama(H_12, im1, im2, delta, delta)

im1 = array(Image.open(imname[0]), "f")
im_02 = warp.panorama(dot(H_12, H_01), im1, im_12, delta, delta)


figure()
imshow(array(im_02, "uint8"))
axis('off')
show()

该代码需要使用PCV库，而PCV的原版库是python2语言写的，而且目前没有更新成python3版本，所以如果使用python3版本的话我们需要找到python3版本的PCV库来安装（或者自己修改），这里附上大佬写的python3版本的PCV库：https://github.com/Li-Shu14/PCV
vscode使用方法：解压后将PCV-master里的PCV文件夹放到代码的同级目录下即可
效果如图：

拍照的时候没有特意为了拼接而进行拍摄，所以看起来很不自然，不过起码拼上了，以后会再补一组效果好的图