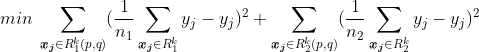sklearn中的决策树（回归）
本文在我的知乎上同步分享：sklearn中的决策树（分类） - 知乎
前面提到，sklearn中的tree模组有DecisionTreeClassifier与DecisionTreeRegressor，前者我们已经详细讨论过了其原理与代码，本文则承接前文的思路，结合具体代码分析回归树的原理。
1 Regression Tree基本概念
相较于分类任务，回归任务的标签是连续的值，所以，我们的目标是利用数据训练出一个好的函数 
，其有着： 
的形式，其中，
，
为输入数据特征的维度， 
是 
空间的一个子空间，
为示性函数，
是 
在 上的取值，但由于是估计，并不知道真值，所以最后其实是求得：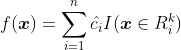
综上，类比分类问题决策树，我们需要一个算法来确定两件事：
1.区域如何划分？
2.区域 上的值 
如何确定？
2 回归问题决策树生成原理
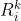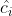2.1 区域 上的值 的确定
我们先来看第二个问题，即在已知区域划分下，我们应该如何确定 ？
由前一篇文章知，在分类问题决策树中，我们根据Gini指数或者信息增益，对于每个特征的每个分类界限值，计算其“纯度”，把能分出最高纯度的那个特征的界限值作为这一步分裂的依据。同理，我们在回归问题中也需要这样一个判断标准，去衡量我们构造的函数与真实值之间的差距。那么对于连续的值，常常选取的标准就是均方误差MSE或平方误差SSE。
设原始数据集为
，
，在给定第一个区域划分之后，如果区域被划分为 
与 
，那么，我们的函数就变为： 
我们的目标就是求解下述优化问题：
等价于求解( 
与 
是变量)： 
上式左右两边在区域分割确定之后互不相关，所以可以分别求最小值，而左右两边都是关于
的二次函数，所以取其对称轴达最小：
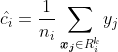，其中 
等于1或2， 
表示在区域 中的样本个数。
那么根据上述公式，我们就确定了区域 上的值 的取值。
2.2 区域 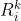的划分
前面一节我们知道了如果区域划分确定，那么 的估计值就是该区域样本标签的平均值。现在考虑如何二分区域。
类似于分类树，假设 
是维行向量，那么每个样本有种特征， ![(\boldsymbol{x_1^T},\dots,\boldsymbol{x_n^T})^T ={ \left[ \begin{array}{ccc} x_{11} & \dots & x_{1k}\\ \vdots & \ddots & \vdots\\ x_{n1} & \dots & x_{nk} \end{array} \right ]}](http://img.e-com-net.com/image/info8/fd9ef3e67c5149cdb88a1e04bea545af.gif)
我们以每个特征的n个值作为划分区域的界限，计算这
种划分对应的SSE，取SSE最小的那种分类对应的特征的值作为当前步的分类标准，即定义：
求解：
得到
坐标对应的划分界限，然后不断进行下去直到某种结束条件触发(达到最大深度、叶子结点样本数达下界等)，最终得到一棵完整的回归树。
3 回归树的python代码
其实，回归树并不适合做回归问题，因为当标签变成连续值后，为了拟合标签，回归树要很茂盛才能在训练集上表现得很好，但是会在测试集上表现得非常差，即过拟合。所以，在尝试用回归树做回归问题时一定要注意剪枝操作，提前设定树的最大深度，ccp_alpha等参数，防止过拟合。
为了方便可视化回归树的一些内容，我这里数据集选取为：
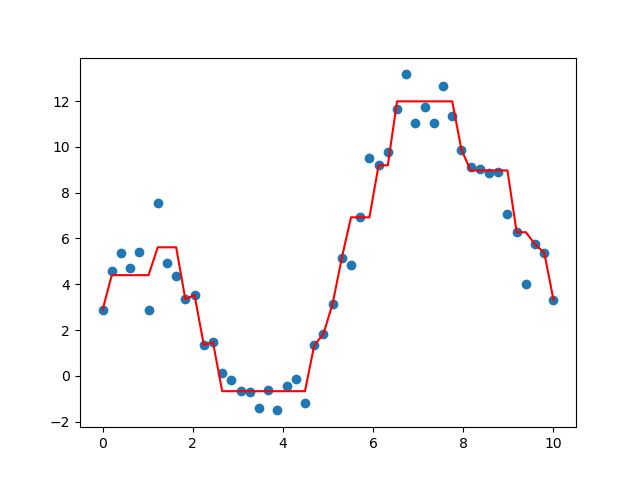
这一函数在(0,10]区间上的50个点， 
为一服从标准正态分布的随机变量，相当于是对原函数的扰动。其散点图如下：
原数据散点图
利用下面的代码，我们可以拟合一个最小二乘回归树，并做可视化：
from sklearn import tree
from sklearn.model_selection import train_test_split
import numpy as np
import matplotlib.pyplot as plt
from io import StringIO
import pydotplus
def f(x, noise=True):
y = 3*np.sin(x) + 4*np.cos(x) + x
if noise:
return y + np.random.randn(len(x))
else:
return y
X = np.linspace(0,10,50)
y = f(X,)
plt.scatter(X,y)
plt.savefig('original.png')
X = np.reshape(X,(-1,1))
X_train, X_test, y_train, y_test =
train_test_split(X, y,test_size=0.2)
tree_model = tree.DecisionTreeRegressor(max_depth=5,
min_samples_leaf=1,
ccp_alpha=0.0,
random_state=111)
tree_model.fit(X_train, y_train)
print(tree_model.score(X_test, y_test))
plt.plot(X, tree_model.predict(X))
plt.savefig('model.png')
dot_data = StringIO()
feature_names = 'x'
tree.export_graphviz(tree_model,
out_file=dot_data,
feature_names=feature_names,
filled=True, rounded=True,
special_characters=True)
graph = pydotplus.graph_from_dot_data(dot_data.getvalue())
graph.write_png("regression_tree.png")得到的回归树函数图像如下：
回归树拟合的函数图像
我们代码中有一步打印score对应的值是0.83，拟合效果还不错。由于得到的回归树很大，我这里就不贴图了。
4 拓展讨论
对于回归树，我们可以去固定训练集、测试集，改变一系列关于回归树的参数，比如最大深度、ccp_alpha的值等，去寻找一个最优的回归树，在前几年有一篇文章提出的AutoML就是利用迭代法在预设定的超参数范围内选择最优机器学习模型，读者可以不妨可视化看看，什么样的树针对上面的数据集有最好的泛化能力。
主要参考
Microstrong：Regression Tree 回归树zhuanlan.zhihu.com
