论文笔记--3D Human Pose Estimation with Spatial and Temporal Transformers（用空间和时间变换器进行三维人体姿势估计）

用空间和时间变换器进行三维人体姿势估计

摘要

  Transformer架构已经成为自然语言处理中的首选模型，现在正被引入计算机视觉任务中，如图像分类、物体检测和语义分割。然而，在人类姿势估计领域，卷积架构仍然占主导地位。在这项工作中，我们提出了PoseFormer，这是一种纯粹的基于变换器的方法，用于视频中的三维人体姿势估计，不涉及卷积架构。受视觉变换器最新发展的启发，我们设计了一个空间-时间变换器结构，以全面模拟每一帧内的人体关节关系以及跨帧的时间相关性，然后输出中心帧的精确三维人体姿势。我们在两个流行的标准基准数据集上对我们的方法进行了定量和定性的评估。Human3.6M和MPI-INF-3DHP。广泛的实验表明，PoseFormer在这两个数据集上都取得了最先进的性能。

1. 简介

  人体姿态估计（HPE）的目的是定位关节，并从图像和视频等输入数据中建立一个身体代表（如骨架位置）。HPE提供了人体的几何和运动信息，可以应用于广泛的领域（如人机交互、运动分析、医疗保健）。目前的工作一般可分为两类：（1）直接估计方法，和（2）二维到三维的提升方法。直接估计方法[31, 29]从二维图像或视频帧中推断出一个三维人体姿态，而不需要立即估计二维姿态的表现。二维到三维的提升方法[25, 5, 43, 38]从中间估计的二维姿态推断出三维人体姿态。受益于最先进的二维姿态检测器的卓越性能，二维到三维提升方法通常优于直接估计方法。然而，这些二维姿态到三维的映射并不简单；由于深度模糊和遮挡，各种潜在的三维姿态可以从同一个二维姿态中产生。为了缓解这些问题并保持自然的一致性，最近的许多工作都将视频的时间信息整合到他们的方法中。例如，[25，5]利用时间卷积神经网络（CNN）来捕捉来自相邻帧的全局依赖性，[33]利用递归架构达到类似的效果。然而，这些架构的时间相关性窗口都是有限的。基于CNN的方法通常依赖于扩张技术，它本身具有有限的时间连通性，而递归网络主要被限制在简单的顺序关联上。
  最近，transformer [37]由于其效率、可扩展性和强大的建模能力，已经成为自然语言处理（NLP）的事实上的模型。由于transformer的自注意力机制，跨长输入序列的全局相关性可以被明显地捕获。这使得它成为一个特别适合序列数据问题的架构，因此自然可扩展到三维HPE。凭借其全面的连接性和表达方式，转化器提供了一个学习更强大的跨帧时间表示的机会。然而，最近的工作[12, 36]表明，转化器需要特定的设计来实现与视觉任务的CNN对应的性能相媲美。具体来说，它们通常需要极大规模的训练数据集[12]，或者如果应用于较小的数据集，则需要增强的数据扩充和正则化[36]。此外，现有的视觉变换器主要限于图像分类[12, 36]、物体检测[4, 50]和分割[41, 47]，但如何利用变换器的力量进行三维HPE仍不清楚。
  为了开始回答这个问题，我们首先在二维到三维的提升HPE上直接应用转换器。在这种情况下，我们将给定序列中每一帧的整个二维姿势视为一个标记（图1（a））。虽然这种基线方法在一定程度上是可行的，但它忽略了空间关系的自然区分（关节到关节），把潜在的改进留在了桌面上。对这一基线的自然扩展是将每个二维关节坐标视为一个标记，并提供一个由序列中所有帧的这些关节组成的输入（图1（b））。然而，在这种情况下，当使用长帧序列时，标记的数量会变得越来越大（在三维HPE中，每帧有17个关节，最多可达243帧，标记的数量将是243×17=4131）。由于转化器计算每个标记对另一个标记的直接注意，模型的内存要求接近一个不合理的水平。

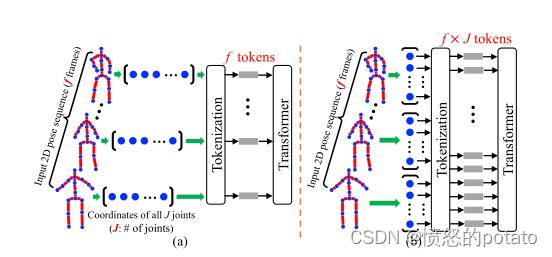
图1. 两种基线方法。

  因此，作为对这些挑战的有效解决方案，我们提出了PoseFormer，这是第一个用于视频中2D到3D提升HPE的纯transformer网络。PoseFormer直接建立了空间和时间方面的模型，这两个维度都有不同的变换器模块。PoseFormer不仅能在空间和时间元素上产生强大的表征，而且对于长的输入序列不会引起巨大的标记数。在高层次上，PoseFormer只是从一个现成的二维姿势估计器中获取检测到的二维姿势序列，并输出中心帧的三维姿势。更具体地说，我们建立了一个空间变换器模块，对每一帧中的二维关节之间的局部关系进行编码。空间自关注层考虑了二维关节的位置信息，并返回该帧的潜在特征表示。接下来，我们的时间转换模块分析每个空间特征表征之间的全局依赖关系，并生成一个精确的三维姿势估计。
  在两个流行的三维HPE基准上进行的实验评估，即Human3.6M[16]和MPI-INF-3DHP[27]，表明PoseFormer在这两个数据集上取得了最先进的性能。我们将我们估计的3D姿势与最先进的方法进行了可视化比较，发现PoseFormer产生了更平滑和更可靠的结果。同时，在消融研究中提供了PoseFormer注意力图的可视化和分析，以了解我们模型的内部工作原理并证明其有效性。我们的贡献有三个方面。

• 我们提出了第一个基于变换器的纯模型–PoseFormer，用于二维到三维提升类别下的三维HPE。
• 我们设计了一个有效的空间-时间变换器模型，其中空间变换器模块编码人体关节之间的局部关系，而时间变换器模块捕捉整个序列中跨帧的全局依赖关系。
• 在没有任何附加条件的情况下，我们的PoseFormer模型在Human3.6M和MPI-INF-3DHP数据集上都取得了最先进的结果。

2. 相关工作

  在此，我们特别总结了三维单人单视角HPE方法。直接估计方法从二维图像中推断出三维人体姿态，而不需要立即估计二维姿态表示。二维到三维的提升方法利用二维姿态作为输入来生成相应的三维姿态，这在该领域的最新方法中比较流行。任何现成的二维姿态估计器都可以与这些方法有效兼容。我们提出的方法PoseFormer也遵循二维到三维的提升管道，因此我们将在本节中主要关注此类方法。
  二维到三维提升的HPE。二维到三维提升方法利用了从输入图像或视频帧中估计的二维姿势。OpenPose[3]、CPN[6]、AlphaPose[13]和HRNet[35]已经被广泛地用作二维姿势检测器。基于这种中间表征，三维姿态可以用各种方法生成。Martinez等人[26]提出了一个简单有效的全连接残差网络，根据单帧的二维关节位置回归三维关节位置。然而，视频可以提供时间信息以提高准确性和鲁棒性，而不是从单眼图像中估计三维人体姿势[49, 10, 32, 8, 2, 44, 38]。Hossain和Little[33]提出了一个使用长短时记忆（LSTM）单元的循环神经网络，以利用输入序列中的时间信息。一些作品[10, 2, 21]利用空间-时间关系和约束条件，如骨长和左右对称来提高性能。Pavllo等人[32]引入了一个时间卷积网络，通过连续的二维序列的二维关键点估计三维姿势。在[32]的基础上，Chen等人[5]增加了骨骼方向模块和骨骼长度模块，以确保各视频帧的时间一致性，Liu等人[25]利用注意机制来识别重要的帧。然而，以前最先进的方法（如[25，5]）依靠扩张的时间卷积来捕获全局依赖性，这在时间连通性方面有内在的限制。此外，这些工作[25, 5, 33, 32]大多使用简单的操作将关节坐标投射到一个潜在的空间，而没有考虑人体关节的运动学相关性。
  三维HPE中的GNNs。当然，人体姿势可以被表示为一个图，其中关节是节点，骨骼是边。图神经网络（GNN）也被应用于二维到三维的姿势提升问题，并提供了很好的性能[9, 45, 24]。Ci等人[9]提出了一个框架，名为局部连接网络（LCNs），它利用完全连接网络和GNN操作来编码局部联合邻域之间的关系。Zhao等人[45]解决了图卷积网络[19]（GCN）操作的一个局限性，特别是如何在节点间共享权重矩阵。引入了语义图卷积操作来学习边的通道权重。
  对于我们的PoseFormer，transformer可以被看作是一种图神经网络，具有独特的、通常是有利的图操作。具体来说，transformer编码器模块基本上形成了一个全连接的图，其中边缘权重是使用输入条件、多头自我注意来计算的。该操作还包括节点特征的归一化，一个跨注意力头输出的前馈聚合器，以及残余连接，这使得它能够有效地扩展堆叠层。与其他图操作相比，这样的操作可以说是有利的。例如，节点之间的连接强度是由transformer的自我注意机制决定的，而不是像这个任务中采用的典型的基于GCN的公式那样，通过邻接矩阵预先定义。这使得模型能够灵活地适应每个输入姿势下各关节的相对重要性。此外，转化器的综合缩放和归一化组件可能有利于减轻许多GNN操作变体在许多层堆叠在一起时的过度平滑效应[48]。
  视觉transformer。最近，人们对将transformer应用于视觉任务产生了兴趣[17, 14]。Carion等人[4]提出了一个用于物体检测和全景分割的DEtection TRansformer（DETR）。Dosovitskiy等人[12]提出了一个纯粹的变换器架构，即视觉变换器（ViT），它在图像分类上实现了最先进的性能。然而，ViT是在大规模数据集ImageNet-21k和JFT300M上训练的，需要大量的计算资源。然后，一个数据高效的图像转换器（DeiT）[36]被提出，它建立在具有知识提炼功能的ViT之上。对于像HPE这样的回归问题，Yang等人[40]提出了一个转化器网络，Transpose，它只从图像中估计二维姿势。Lin等人[23]在他们的方法METRO（MEsh TRansfOrmer）中结合了CNN和transformer器网络，从单一图像中重建三维姿势和网格顶点。与我们的方法相比，METRO属于直接估计的范畴。另外，METRO忽略了时间上的一致性，这限制了其估计的稳健性。我们的空间-时间变换器架构利用了每一帧的关键点相关性，并保留了视频中的自然时间一致性。

3. 方法

图2. (a) 时间变换器基线。(b) 空间-时间变换器（PoseFormer）架构，由三个模块组成。空间变换器模块用于提取特征，考虑到每个单独骨架的关节关联性。一个时间转换模块，用于学习整个序列的全局依赖关系。一个回归头模块对中心帧的最终三维姿势进行回归。变换器编码器的说明是按照ViT[12]进行的。

  我们遵循与[26, 32, 25, 5]相同的视频中3D HPE的2D-3D提升管道。每一帧的二维姿态由一个现成的二维姿态检测器获得，然后将连续帧的二维姿态序列作为估计中心帧三维姿态的输入。与之前基于CNN的最先进的模型相比，我们产生了一个极具竞争力的无卷积变换器网络。

3.1. 时间变换器基线

  作为transformer在二维到三维提升中的基准应用，我们将每个二维姿势视为一个输入标记，并采用转换器来捕捉输入之间的全局依赖关系，如图2(a)所示。我们将每个输入标记称为一个patch，与ViT[12]的术语相似。对于输入序列$X\in R^{f\times \left(J\cdot 2\right)}$，$f$是输入序列的帧数，$J$是每个二维姿势的关节数，2表示二维空间中的关节坐标。$\left\{X^i\in {\mathbb{R}}^{1\times \left(J\cdot 2\right)}|i=1,2,...,f\right\}$表示每帧的输入向量。补丁嵌入(patch embedding)是一个可训练的线性投影层，将每个patch嵌入到一个高维特征。transformer网络利用位置嵌入(positional embeddings )来保留序列的位置信息。该程序可以被表述为
$$Z_0=\left[X^{1}E;X^{2}E;...;X^{f}E\right]+E_{pos}\left(1\right)$$
  在通过线性投影矩阵$E\in {\mathbb{R}}^{\left(J\cdot 2\right)\times C}$嵌入并与位置嵌入$E_{pos}\in {\mathbb{R}}^{f\times C}$相加后，输入序列$X\in {\mathbb{R}}^{f\times \left(J\cdot 2\right)}$成为$Z_0\in {\mathbb{R}}^{f\times C}$，其中$C$是嵌入维度。$Z_0$被送到时态变换器编码器(Temporal Transformer Encoder)。
  作为变换器的核心功能，自我注意被设计为将输入序列的不同位置与嵌入式特征联系起来。我们的变换器编码器是由多头自我注意块(Multi-head Self Attention blocks )与多层感知器（MLP）块组成的，如[12]。LayerNorm在每个块之前应用，剩余连接在每个块之后应用[39, 1]。
  Scaled Dot-Product Attention可以被描述为一个映射函数，它将查询矩阵$Q$、关键矩阵$K$和价值矩阵$V$映射到输出注意力矩阵。$Q,K,V\in {\mathbb{R}}^{N\times d}$，其中$N$是序列中的向量数，$d$是维度。在这个注意力操作中，利用了一个缩放系数来进行适当的归一化，以防止当$d$的大值导致点乘的幅度变大时出现极小的梯度。因此，因此，缩放点积的输出注意可以表示为：
$$Attention\left(Q,K,V\right)=Soft\max \left(Q{K}^{\top }/\sqrt{d}\right)V\left(2\right)$$
  在我们的时间变换器(temporal transformer)中，$d=C$，$N=f$。$Q$、$K$和$V$是通过线性变换$W_Q$、$W_K$和 $W_V\in {\mathbb{R}}^{C\times C}$从嵌入特征$Z\in {\mathbb{R}}^{f\times C}$计算出来的。
$$Q=Z{W}_Q,K=Z{W}_K,V=Z{W}_V\left(3\right)$$
  Multi-head Self Attention Layer(MSA)利用多个head来联合模拟来自不同位置的代表子空间的信息。每个head平行地应用Scaled Dot-Product Attention。MSA的输出将是h个注意力head输出的串联。
$$MSA\left(Q,K,V\right)=Comcat\left(H_1,H_2,...,H_h\right)W_{out}\left(4\right)$$
$$where{H}_i=Attention\left(Q_i,K_i,V_i\right),i\in \left[1,...,h\right]\left(5\right)$$
考虑到我们的嵌入特征$Z_0\in {\mathbb{R}}^{f\times C}$，L层的时态变换器编码器(Temporal Transformer Encoder)结构可以表示如下：
$$Z_{\ell }^{{}^{\prime }}=MSA\left(LN\left(Z_{\ell -1}\right)\right)+Z_{\ell -1},\ell =1,2...L\left(6\right)$$
$$Z_{\ell }=MLP\left(LN\left(Z_{\ell }^{{}^{\prime }}\right)\right)+Z_{\ell }^{{}^{\prime }},\ell =1,2...L\left(7\right)$$
$$Y=LN\left(Z_L\right)\left(8\right)$$
  其中$LN\left(\cdot \right)$表示层归一化算子（与ViT中相同）。时间变换器编码器由$L$个相同的层组成，编码器输出$Y\in {\mathbb{R}}^{f\times C}$与编码器输入$Z_0\in {\mathbb{R}}^{f\times C}$保持相同大小。
  为了预测中心帧的三维姿态，编码器输出$Y\in {\mathbb{R}}^{f\times C}$通过取帧维度的平均值缩减为向量$y\in {\mathbb{R}}^{1\times C}$。最后，一个MLP模块将输出回归到$y\in {\mathbb{R}}^{1\times \left(J\cdot 3\right)}$，这就是中心帧的三维姿势。

3.2. 姿势变换器:空间-时间变换器(PoseFormer: Spatial-Temporal Transformer)

  我们观察到，时间变换器基线主要关注输入序列中帧之间的全局依赖关系。补丁嵌入(patch embedding)，一个线性变换，被用来投射关节坐标到一个隐藏的维度。然而，局部关节坐标之间的运动学信息在时间变换器基线中没有得到有力的体现，因为简单的线性投影层不能学习注意力信息。一个潜在的变通方法是将每个关节坐标视为一个单独的patch，并将所有帧的关节作为输入送入转化器（见图1（b））。然而，patch的数量会迅速增加（帧数f乘以关节数J），导致模型的计算复杂性为$O\left({\left(f\cdot J\right)}^2\right)$。例如，如果我们对每个二维姿势使用81个帧和17个关节，patch的数量将是1377个（ViT模型使用576个patch（输入尺寸=384×384，patch尺寸=16×16））。
  为了有效地学习局部联合关联，我们采用了两个分离的transformers，分别用于空间和时间信息。如图2（b）所示，PoseFormer由三个模块组成：空间变换器模块(spatial transformer module)、时间变换器模块( temporal transformer)和回归头模块( regression head module)。
  空间变换器模块(Spatial Transformer Module)。空间转换模块是为了从单帧中提取高维的特征嵌入。给定一个具有$J$个关节的二维姿势，我们将每个关节（即两个坐标）视为一个patch，并遵循一般的视觉变换器管道，在所有patch中进行特征提取。首先，我们用可训练的线性投影将每个关节的坐标映射到一个高维度，这被称为空间补丁嵌入。我们将其与可学习的空间位置嵌入[12]$E_{SPos}\in {\mathbb{R}}^{J\times c}$相加，因此第i帧的输入$X_i\in {\mathbb{R}}^{1\times \left(J\cdot 2\right)}$成为$z_0^i\in {\mathbb{R}}^{J\times c}$，其中$2$表示每一帧的二维坐标，$c$是空间嵌入的维度。所得的关节特征序列被送入空间变换器编码器，该编码器应用自我注意机制来整合所有关节的信息。对于第$i$帧，具有$L$层的空间变换器编码器的输出将是$z_L^i\in {\mathbb{R}}^{J\times c}$。
  时间变换器模块(Temporal Transformer Module)。由于空间变换器模块(spatial transformer module)对每一帧的高维特征进行编码，时间变换器模块的目标是对整个帧序列的依赖关系进行建模。对于第$i$帧，空间变换器$z_L^i\in {\mathbb{R}}^{J\times c}$的输出被平铺为向量$z^i\in {\mathbb{R}}^{1\times \left(J\cdot c\right)}$。然后我们将这些来自$f$个输入帧的向量$\left\{z^1,z^2,...,z^f\right\}$连接起来，作为$Z_0\in {\mathbb{R}}^{f\times \left(J\cdot c\right)}$。在时间变换器模块之前，我们添加可学习的时间位置嵌入[12] $E_{TPos}\in {\mathbb{R}}^{f\times \left(J\cdot c\right)}$，以保留帧的位置信息。对于时间变换器编码器(temporal transformer encoder)，我们采用与空间变换器编码器相同的结构，它由多头自我注意块和$MLP$块组成。时空变换器模块的输出是$Y\in {\mathbb{R}}^{f\times \left(J\cdot c\right)}$。
  回归头(Regression Head)。由于我们使用一连串的帧来预测中心帧的三维姿势，时间变换器模块(temporal transformer module)的输出$Y\in {\mathbb{R}}^{f\times \left(J\cdot c\right)}$需要被还原为$y\in {\mathbb{R}}^{1\times \left(J\cdot c\right)}$。我们在帧的维度上应用加权平均运算（用学到的权重）来实现这一点。最后，一个具有$Layernorm$和一个线性层的简单$MLP$模块返回输出$y\in {\mathbb{R}}^{1\times \left(J\cdot 3\right)}$，这是中心帧的预测三维姿势。
  损失函数。为了训练我们的时空转换模型，我们应用标准的$MPJPE$（平均每关节位置误差）损失来最小化预测姿势和地面真实姿势之间的误差，即
$$\mathcal{L}=\frac{1}{J}\sum _{k=1}^J\Vert p_k-{\hat{p}}_k{\Vert }_2\left(9\right)$$

其中$p_k$和${\hat{p}}_k$分别是第$k$个关节的地面真相和估计的三维关节位置。

4. 实验

4.1. 数据集和评估指标

  我们在两个常用的三维HPE数据集上评估我们的模型，Human3.6M[16]和MPI-INF-3DHP[27]。
Human3.6M[16]是最广泛使用的三维单人HPE的室内数据集。有11位专业演员表演了17个动作，如坐、走、讲电话等。每个主体的视频都是从室内环境中的4个不同角度录制的。这个数据集包含了360万个视频帧，这些视频帧带有由精确的基于标记的运动捕捉系统捕获的三维地面真实注释。按照以前的工作[32, 25, 5]，我们采用相同的实验设置：所有15个动作都用于训练和测试，模型在五个部分（S1, S5, S6, S7, S8）上进行训练，并在两个主体（S9和S11）上进行测试。
  MPI-INF-3DHP[27]是一个更具挑战性的3D姿势数据集。它包含了受限的室内场景和复杂的室外场景。有8个演员从14个摄像机视角执行8个动作，涵盖了更多的姿势多样性。MPI-INF-3DHP提供了一个由6个不同场景的主体组成的测试集。我们遵循[22, 5, 38]中的设置。
  对于Human3.6M数据集，我们使用最常用的评估指标（MPJPE和P-MPJPE）[46]来评估我们对地面真实三维姿势的估计性能。MPJPE（平均每关节位置误差）被计算为估计的关节和地面真实之间的平均欧氏距离，单位为毫米；我们把MPJPE称为协议1。P-MPJPE是通过对估计的三维姿态和地面实况进行后处理后的MPJPE，它对单个关节的预测失败更为稳健。我们将P-MPJPE称为协议2。
  对于MPI-INF-3DHP数据集，我们使用MPJPE、150mm范围内的正确关键点百分比（PCK）[22, 5, 38]，以及曲线下面积（AUC）。

4.2. 实施细节

  我们用Pytorch[30]实现了我们提出的方法。两个NVIDIA RTX 3090 GPU被用于训练和测试。在进行实验时，我们选择了三种不同的帧序列长度，即f=9、f=27、f=81。关于帧数与结果的细节将在消融研究中讨论（第4.4节）。我们按照[32, 25, 5]在训练和测试中应用水平翻转的姿势作为数据增强。我们使用Adam[18]优化器对我们的模型进行了130个历时的训练，权重衰减为0.1。我们采用指数学习率衰减计划，初始学习率为2e-4，每个历时的衰减系数为0.98。我们将批次大小设置为1024，并采用随机深度[15]，对变换器编码器层的速率为0.1。对于二维姿势检测器，我们按照[32, 25, 5]在Human3.6M上使用级联金字塔网络（CPN）[7]，并按照[28, 22]将地面真实二维姿势作为MPI-INF-3DHP的输入。

4.3. 与最新技术水平的比较

  Human3.6M。我们在表1中报告了测试集（S9和S11）的所有15个动作结果。最后一栏提供了所有测试集的平均性能。按照从二维到三维的提升方法，我们使用CPN网络作为二维姿势检测器，然后将检测到的二维姿势作为输入进行训练和测试。在协议1和协议2下，PoseFormer比我们的基线（即第3.1节中的时间变换器基线）要好很多（6.1%和6.4%）。这清楚地表明了使用空间变换器对每一帧中的关节之间的相关性进行表达式建模的优势。如表1（顶部）所示，PoseFormer在协议1下产生的平均MPJPE最低，为44.3mm。与基于变换器的方法METRO[23]相比，PoseFormer将MPJPE降低了约18%，因为METRO忽略了时间上的一致性，因为三维姿势是由单一图像估计的。对于协议2，我们也获得了最佳的整体结果，如表1（底部）所示。此外，PoseFormer在困难的动作上实现了更准确的姿势预测，如Photo、SittingDown、WalkDog和Smoke。与其他简单的动作不同，这些动作中的姿势变化更快，一些长距离的帧有很强的相关性。在这种情况下，全局依赖性起着重要的作用，而转化器的注意机制则特别有优势。
  为了进一步研究我们方法的下限，我们直接使用地面真实的二维姿势作为输入，以减轻由嘈杂的二维姿势数据引起的误差。结果显示在表2中。通过使用干净的二维姿势数据，MPJPE从44.3mm减少到31.3mm，约为29.7%。PoseFormer在9个动作中取得了最佳得分，在6个动作中取得了第二好的得分。与SRNet[43]相比，平均得分提高了约2%。

表1. 使用检测到的二维姿势作为输入，在协议1和2下对Human3.6M的估计三维姿势和地面真实三维姿势之间的平均每关节位置误差的定量比较。上表：协议1（MPJPE）下的结果。下表：协议2（P-MPJPE）下的结果。f表示每种方法使用的输入帧数，∗表示输入的2D姿势由级联金字塔网络（CPN）检测，†表示基于变形器的模型。(红色：最佳；蓝色：次佳)

  在图3中，我们还比较了在Human3.6M测试集S11上误差最大的一些单个关节的MPJPE与动作照片。PoseFormer在这些困难的关节上取得了比[32, 5]更好的性能。
  MPI-INF-3DHP。表3报告了PoseFormer与其他方法在MPI-INF-3DHP上的定量结果。与Human3.6M相比，这个数据集包含的训练样本较少，而且有些样本来自于室外场景。由于该数据集的序列长度通常较短，我们使用9帧的2D姿势作为我们的模型输入。我们的方法在所有三个评估指标（PCK、AUC和MPJPE）上再次取得了最佳表现。

图3. 在Human3.6M测试集S11的所有帧中，与照片动作的平均联合误差比较。

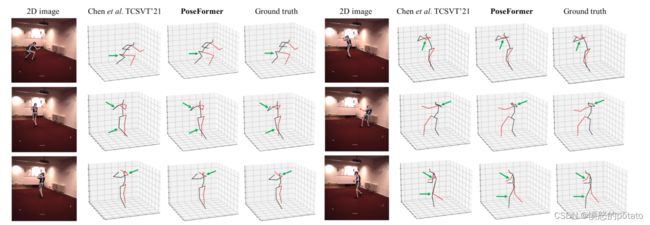
  定性结果。我们还提供了三维估计姿态和地面实况之间的视觉比较。我们在Human3.6M测试集S11上对PoseFormer进行了评估，该测试集是最具挑战性的动作之一（所有方法的MPJPE都很高）。与最先进的方法[5]相比，我们的PoseFormer实现了更准确的预测，如图4所示。

4.4. 消融研究

  为了验证PoseFormer各个部分的贡献以及超参数对性能的影响，我们在协议1下用Human3.6M数据集进行了广泛的消融实验。
  PoseFormer的设计。我们研究了空间变换器的影响，以及表4中空间和时间变换器的位置嵌入。我们输入9帧CPN检测到的2D姿势（J=17）来预测3D姿势。为了公平地比较每个模块的影响，所有的结构参数都是固定的；空间变换器的嵌入尺寸是17×32=544，空间变换器编码器层的数量是4。 对于时间变换器，嵌入尺寸与空间变换器一致（即544），我们也应用4个时间变换器层。为了验证我们的空间-时间设计的影响，我们首先与我们在第3.1节开始的转化器基线进行比较。表4中的结果表明，我们的空间-时间变换器产生了重大影响（从52.5到49.9MPJPE），因为联合相关关系被更有力地模拟了。这也与表1中f=81时的结果（Baseline vs. PoseFormer）一致。接下来，我们评估位置嵌入的影响。我们探索了四种可能的组合：没有位置嵌入，只有空间位置嵌入，只有时间位置嵌入，以及空间和时间位置嵌入。比较这些组合的结果，很明显，位置嵌入提高了性能。通过在空间和时间模块上应用这些东西，达到了最佳的整体效果。

表2. 在协议1（MPJPE）下的Human3.6M数据集上，使用地面真实2D姿势作为输入，估计的3D姿势和地面真实3D姿势之间的平均每关节位置误差的定量比较。(红色：最佳；蓝色：次佳)

图4. 我们的方法（PoseFormer）和Chen等人的SOTA方法[5]在Human3.6M测试集S11上的照片动作的定性比较。绿色箭头强调了PoseFormer明显具有更好结果的位置。

表3. 与以前的MPIINF-3DHP方法的定量比较。最好的分数用粗体字标出。

表4. 对PoseFormer中不同组件的消融研究。评估是在Human3.6M（协议1）上进行的，使用检测到的2D姿势作为输入。(T: 只有时间上的；S-T: 空间-时间上的)

表5. 对PoseFormer中不同结构参数的消融研究。评估是在Human3.6M（协议1）上进行的，使用检测到的二维姿势作为输入。c是空间变换器补丁嵌入维度。LS和LT分别表示空间和时间变换器的层数。

表6. 计算复杂性、MPJPE和推理速度（每秒一帧（FPS））的比较。评估是在协议1下对Human3.6M进行的，使用检测到的2D姿势作为输入。FPS是基于单个GeForce GTX 2080 Ti GPU。

  架构参数分析。我们探索各种参数组合，以找到表5中的最佳网络结构。c代表空间变换器中的嵌入特征维度，L表示变换器编码器中使用的层数。在PoseFormer中，空间变换器的输出被压扁，并与时间位置嵌入相加，形成时间变换器编码器的输入。因此，时间变换器编码器的嵌入特征维度是c×J。我们模型的最佳参数是c=32，LS=4，LT=4。
  计算复杂性分析。我们在表6中报告了不同输入序列长度（f）下的模型性能、参数总数和每帧估计浮点运算（FLOPs），以及输出帧/秒（FPS）的数量。当序列长度增加时，我们的模型取得了更好的准确性，而参数总数并没有增加很多。这是因为帧数只影响到时间位置嵌入层，它不需要很多参数。与其他模型相比，我们的模型需要的总参数较少，性能也很有竞争力。我们报告了不同模型在单个GeForce RTX 2080 Ti GPU上的推理FPS，遵循[5]中的相同设置。尽管我们模型的推理速度不是绝对最快的，但对于实时推理来说，其速度还是可以接受的。对于完整的3D HPE处理，首先由2D姿势检测器检测2D姿势，然后由我们的方法估计3D姿势。普通二维姿势检测器的FPS通常低于80，这意味着我们模型的推理速度不会成为瓶颈。

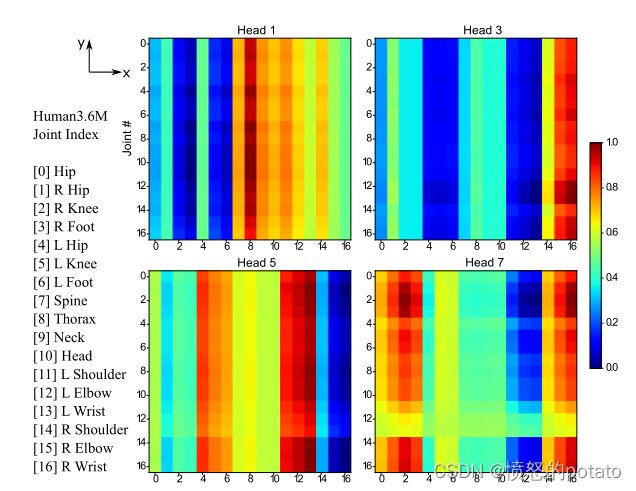
图5. 空间变换器中的自我关注的可视化。x轴（水平）和y轴（垂直）分别对应于查询和预测的输出。像素wi,j（i：行，j：列）表示第j个查询对第i个输出的关注权重。红色表示更强的注意力。注意力输出从0到1被规范化。

图6. 时空变换器中自我注意力的可视化。X轴（水平）和Y轴（垂直）分别对应于查询和预测的输出。像素wi,j（i：行，j：列）表示第j个查询对第i个输出的关注权重。红色表示更强的注意力。注意力输出从0到1被规范化。

  注意力的可视化。为了通过多头自我注意块来说明注意机制，我们在Human3.6M测试集S11上对一个特定动作（SittingDown）进行了评估，并将来自空间和时间变换器的自我注意图分别可视化，如图5和图6所示。对于空间自我注意图，X轴对应于17个关节的查询，Y轴表示注意力的输出。如图5所示，注意头返回不同的注意强度，这代表了在输入关节之间学到的各种局部关系。我们发现，头3关注的是15和16号关节，也就是右肘和右腕。头5建立了左腿和左臂的连接（4、5、6号关节和11、12、13号关节）。这些关节可以被归类为身体的左侧部分，而头7集中在右侧（关节1、2、3与关节12、13、14）。
  对于图6中的时间性自我注意图，X轴对应于81帧的查询，Y轴表示注意的输出。长期的全局依赖性是由不同的注意力头学习的。头3的注意力与中心帧右侧的一些帧（如第58、62和69帧）高度相关。头7捕捉到了第1、20、22、42、78帧的依赖关系，尽管它们的距离很远。空间和时间注意力图表明，PoseFormer成功地模拟了关节之间的局部关系，同时也捕捉到了整个输入序列的长期全局依赖关系。

表7. 对HumanEva测试集的MPJPE评估。FT表示在Human3.6M上使用预训练的模型进行微调。

  对小数据集的泛化。之前的工作，如[12]，得出的结论是，在数据量不足的情况下训练的转化器不能很好地进行泛化。我们用我们的模型进行了一个实验，以研究在一个小数据集–HumanEva[34]上的转化器学习能力。与Human3.6M（大于100万帧）相比，它是一个小得多的数据集（小于50K帧）。表7显示了从头开始训练以及在Human3.6M上使用预训练模型进行微调的结果。我们发现，在微调时，性能可以提高很大的幅度，这遵循了以前的观察[12, 36]，即变压器在大规模数据集上预训练时可以表现良好。

5. 总结

  在本文中，我们提出了PoseFormer，一种基于纯变换器的方法，用于从二维视频中进行三维姿势估计。空间变换器模块对二维关节之间的局部关系进行编码，时间变换器模块捕捉任意帧之间的全局依赖关系，而不考虑距离。广泛的实验表明，我们的模型在两个流行的三维姿势数据集上实现了最先进的性能。