【聚类】专题总结——概览 + 划分聚类
目录
一、 聚类的概念
二、聚类分析中需要考虑的关键问题:
三、详细介绍
1. 数据相似性
2. 聚类优化方法
(1)划分聚类(partitioning clustering)
(2)层次聚类(hierarchical clustering)
(3)基于数据密度的聚类(density based clustering)
(4)基于空间网格的聚类(grid based clustering)
(5)基于统计模型的聚类(model based clustering)
(6)基于图的聚类(graph based clustering)
(7)基于神经网络的聚类(neural network based clustering)
2.1 划分聚类(partitioning clustering)
1)K-means聚类方法
2)K-中心点聚类
=> CLARA(clustering large application)
一、 聚类的概念
指根据数据之间的相似性,将数据集合分成若干个子集,每个子集被称为簇cluster,每个簇是从数据中自动发现的具有共同特性的一类数据。
聚类结果反映了训练数据的分布规律,即可直接用数据分组结果来反映这种分布规律,也可进一步将簇中数据拟合为相应的统计分布。
聚类结果由数据点到簇的归属来决定,其隶属度(membership)有明确的和模糊的两种。 明确的隶属度为1或0,表示是否隶属。——对应硬聚类(hard clustering)
模糊的隶属度取值在区间[0,1]之间,表示隶属的程度。——软聚类(soft clustering,或模糊聚类fuzzy clustering)
聚类问题可以归结为一个从数据的所有不同组合方案中寻找最优组合的组合优化(combinational optimization)问题。
二、聚类分析中需要考虑的关键问题:
1. 数据相似性
2. 聚类优化方法
3. 可伸缩性问题
4. 聚类形状(clustering shape)
5. 局外点问题
三、详细介绍
1. 数据相似性
在定义聚类优化目标时,基本准则是簇内数据相似、簇间数据不相似。
以几何方式度量相似性——距离.
常用距离计算公式
| 名称 | 计算公式 |
| 欧式(Euclidean) | 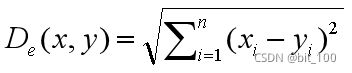 |
| 曼哈顿(City block/Manhattan) | 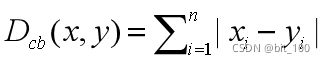 |
| 闵可夫斯基距离(Minkowski) |  |
| 契比雪夫(Chebyishev) |  |
| 马氏距离(mahalanobis) |  |
| ... | .......... |
2. 聚类优化方法
(1)划分聚类(partitioning clustering)
划分聚类方法直接将数据集划分为相应的子集,每个子集为一个簇。其中子集的个数通常是指定的。划分聚类的过程是一种从所有可能的划分方案中搜索一个最优方案的过程,关键在于划分方案的搜索方法。
(2)层次聚类(hierarchical clustering)
通过数据的分解与合并来实现聚类,计算过程一种由单个数据合并成小簇,由小簇再合并成较大的簇,由较大的簇再合并成更大的簇的逐渐合并过程,或与之相反的逐渐分解过程。
(3)基于数据密度的聚类(density based clustering)
用距离来度量数据之间的相似性,则簇内数据应该尽可能紧密,簇间数据应该尽可能稀疏。关键问题是如何定义数据密度及其实现。
(4)基于空间网格的聚类(grid based clustering)
此类方法将数据所在空间分为不同尺度下的网格,按网格来组织数据,在此基础上那个利用网格内数据的统计信息实现聚类,其中往往还需考虑数据的密度。
优点:网格的划分与数据个数无关,计算性能不收数据个数的影响,适应不同规模数据集。
(5)基于统计模型的聚类(model based clustering)
该方法认为每个簇中数据应该服从一个特定的统计分布,因此将数据拟合成若干统计分布,每个分布表示一个簇。在此基础上,根据数据到簇的类条件概率密度完成聚类。不同统计模型方法不同。
(6)基于图的聚类(graph based clustering)
利用图来表示数据之间的相似关系,其中节点代表数据,节点间边的权重为数据之间的相似度,进而通过对于图的操作,来完成聚类。一般先构造完全图(complete graph),然后简化为稀疏图(sparse graph),进行聚类。
(7)基于神经网络的聚类(neural network based clustering)
利用自组织特征映射网等具备聚类能力的网络来实现聚类。
其他: 引入核函数来提高数据可分性的核聚类(kernel clustering)。在原始空间的子空间上有明显的分簇特性,则在数据子空间进行聚类的子空间聚类算法(Subspace clustering)。
2.1 划分聚类(partitioning clustering)
划分聚类方法直接将数据集划分为相应的子集,每个子集为一个簇。其中子集的个数通常是指定的。划分聚类的过程是一种从所有可能的划分方案中搜索一个最优方案的过程,关键在于划分方案的搜索方法。
1)K-means聚类方法
用簇中所有数据的均值向量代表每个簇,以数据与簇均值之间的距离作为数据到簇的距离,然后将每个数据划分到离它最近的簇。优化目标是使得各个数据到其隶属的簇均值之间的距离之和最小化。
优点:简单、易实现;可以保证收敛到局部最优;具有多项式时间复杂度。
缺点:局部最优算法,容易受到初始均值影响;采用均值来代表簇不够稳健,易受噪声影响;需要事先给定聚类的个数。
2)K-中心点聚类
不断用非中心点数据代替中心点数据,以提高聚类质量,直至找到最合适的中心点,代表一个簇。
优点:与数据均值相比,代表性数据点不易受噪声的影响,更加鲁棒,
缺点:计算复杂度更高。
=> CLARA(clustering large application)
利用抽样技术提高计算效率,并非在整个数据集合上执行k-中心点算法。
- 首先进行抽样得到数据子集,
- 然后在数据子集上执行k-中心点获得中心点,
- 最后将整个数据集合上的数据按其与各中心点的距离分配至最近的簇。
- 可多次抽样降低抽样不理想影响。
聚类系列总结第一篇,时间仓促,再加上划分聚类的k-means和k-中心点聚类比较简单,所以写的也比较简单。后面的慢慢写详细。