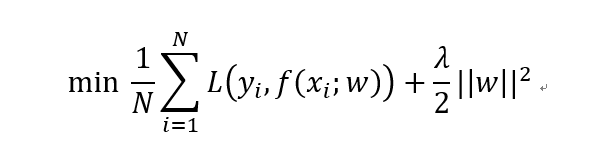数学推导+纯Python实现机器学习算法14：Ridge岭回归

点击上方“小白学视觉”，选择加"星标"或“置顶”

重磅干货，第一时间送达

     上一节我们讲到预防过拟合方法的Lasso回归模型，也就是基于L1正则化的线性回归。本讲我们继续来看基于L2正则化的线性回归模型。

L2正则化

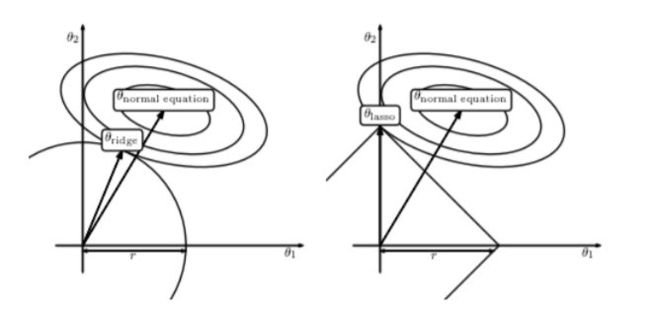
     相较于L0和L1，其实L2才是正则化中的天选之子。在各种防止过拟合和正则化处理过程中，L2正则化可谓第一候选。L2范数是指矩阵中各元素的平方和后的求根结果。采用L2范数进行正则化的原理在于最小化参数矩阵的每个元素，使其无限接近于0但又不像L1那样等于0，也许你又会问了，为什么参数矩阵中每个元素变得很小就能防止过拟合？这里我们就拿深度神经网络来举例说明吧。在L2正则化中，如何正则化系数变得比较大，参数矩阵W中的每个元素都在变小，线性计算的和Z也会变小，激活函数在此时相对呈线性状态，这样就大大简化了深度神经网络的复杂性，因而可以防止过拟合。

     加入L2正则化的线性回归损失函数如下所示。其中第一项为MSE损失，第二项就是L2正则化项。

      L2正则化相比于L1正则化在计算梯度时更加简单。直接对损失函数关于w求导即可。这种基于L2正则化的回归模型便是著名的岭回归(Ridge Regression)。

Ridge

     有了上一讲的代码框架，我们直接在原基础上对损失函数和梯度计算公式进行修改即可。下面来看具体代码。

导入相关模块：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split

读入示例数据并划分：

data = pd.read_csv('./abalone.csv')
data['Sex'] = data['Sex'].map({'M':0, 'F':1, 'I':2})
X = data.drop(['Rings'], axis=1)
y = data[['Rings']]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25)
X_train, X_test, y_train, y_test = X_train.values, X_test.values, y_train.values, y_test.values
print(X_train.shape, y_train.shape, X_test.shape, y_test.shape)

模型参数初始化：

# 定义参数初始化函数
def initialize(dims):
    w = np.zeros((dims, 1))
    b = 0
    return w, b

定义L2损失函数和梯度计算：

# 定义ridge损失函数
def l2_loss(X, y, w, b, alpha):
    num_train = X.shape[0]
    num_feature = X.shape[1]
    y_hat = np.dot(X, w) + b
    loss = np.sum((y_hat-y)**2)/num_train + alpha*(np.sum(np.square(w)))
    dw = np.dot(X.T, (y_hat-y)) /num_train + 2*alpha*w
    db = np.sum((y_hat-y)) /num_train
    return y_hat, loss, dw, db

定义Ridge训练过程：

# 定义训练过程
def ridge_train(X, y, learning_rate=0.001, epochs=5000):
    loss_list = []
    w, b = initialize(X.shape[1])
    for i in range(1, epochs):
        y_hat, loss, dw, db = l2_loss(X, y, w, b, 0.1)
        w += -learning_rate * dw
        b += -learning_rate * db
        loss_list.append(loss)
        
        if i % 100 == 0:
            print('epoch %d loss %f' % (i, loss))
        params = {
            'w': w,
            'b': b
        }
        grads = {
            'dw': dw,
            'db': db
        }
    return loss, loss_list, params, grads

执行示例训练：

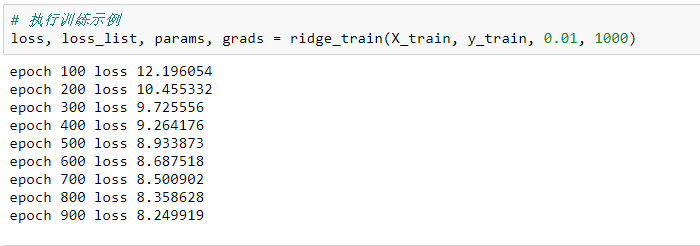
# 执行训练示例
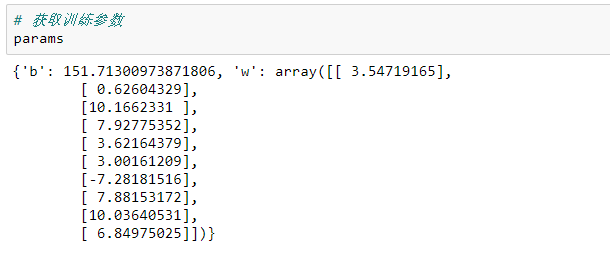
loss, loss_list, params, grads = ridge_train(X_train, y_train, 0.01, 1000)

模型参数：

定义模型预测函数：

# 定义预测函数
def predict(X, params):
    w
 = 
params
[
'w'
]
    b = params['b']
    
    y_pred = np.dot(X, w) + b
    return y_pred


y_pred = predict(X_test, params)
y_pred[:5]

测试集数据和模型预测数据的绘图展示：

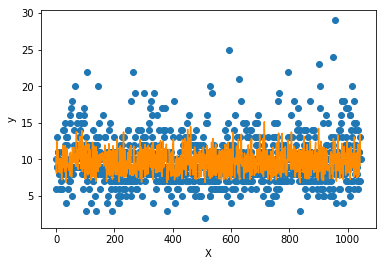
# 简单绘图
import matplotlib.pyplot as plt
f = X_test.dot(params['w']) + params['b']


plt.scatter(range(X_test.shape[0]), y_test)
plt.plot(f, color = 'darkorange')
plt.xlabel('X')
plt.ylabel('y')
plt.show();

     可以看到模型预测对于高低值的拟合较差，但能拟合大多数值。这样的模型相对具备较强的泛化能力，不会产生严重的过拟合问题。

最后进行简单的封装：

import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split


class Ridge():
    def __init__(self):
        pass
        
    def prepare_data(self):
        data = pd.read_csv('./abalone.csv')
        data['Sex'] = data['Sex'].map({'M': 0, 'F': 1, 'I': 2})
        X = data.drop(['Rings'], axis=1)
        y = data[['Rings']]
        X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25)
        X_train, X_test, y_train, y_test = X_train.values, X_test.values, y_train.values, y_test.values
        return X_train, y_train, X_test, y_test
    
    def initialize(self, dims):
        w = np.zeros((dims, 1))
        b = 0
        return w, b


    def l2_loss(self, X, y, w, b, alpha):
        num_train = X.shape[0]
        num_feature = X.shape[1]
        y_hat = np.dot(X, w) + b
        loss = np.sum((y_hat - y) ** 2) / num_train + alpha * (np.sum(np.square(w)))
        dw = np.dot(X.T, (y_hat - y)) / num_train + 2 * alpha * w
        db = np.sum((y_hat - y)) / num_train
        return y_hat, loss, dw, db


    def ridge_train(self, X, y, learning_rate=0.01, epochs=1000):
        loss_list = []
        w, b = self.initialize(X.shape[1])
        for i in range(1, epochs):
            y_hat, loss, dw, db = self.l2_loss(X, y, w, b, 0.1)
            w += -learning_rate * dw
            b += -learning_rate * db
            loss_list.append(loss)
        
            if i % 100 == 0:
                print('epoch %d loss %f' % (i, loss))
            params = {
                'w': w,
                'b': b
            }
            grads = {
                'dw': dw,
                'db': db
            }
        return loss, loss_list, params, grads
    
    
    def predict(self, X, params):
        w = params['w']
        b = params['b']
        y_pred = np.dot(X, w) + b
        return y_pred
    
 
if __name__ == '__main__':
    ridge = Ridge()
    X_train, y_train, X_test, y_test = ridge.prepare_data()
    loss, loss_list, params, grads = ridge.ridge_train(X_train, y_train, 0.01, 1000)
    print(params)

sklearn中也提供了Ridge的实现方式：

# 导入线性模型模块
from sklearn.linear_model import Ridge
# 创建Ridge模型实例
clf = Ridge(alpha=1.0)
# 对训练集进行拟合
clf.fit(X_train, y_train)
# 打印模型相关系数
print("sklearn Ridge intercept :", clf.intercept_)
print("\nsklearn Ridge coefficients :\n", clf.coef_)

     以上就是本节内容，下一节我们将延伸树模型，重点关注集成学习和GBDT系列。

更多内容可参考笔者GitHub地址：

https://github.com/luwill/machine-learning-code-writing

代码整体较为粗糙，还望各位不吝赐教。

好消息！

小白学视觉知识星球

开始面向外开放啦

下载1：OpenCV-Contrib扩展模块中文版教程

在「小白学视觉」公众号后台回复：扩展模块中文教程，即可下载全网第一份OpenCV扩展模块教程中文版，涵盖扩展模块安装、SFM算法、立体视觉、目标跟踪、生物视觉、超分辨率处理等二十多章内容。


下载2：Python视觉实战项目52讲
在「小白学视觉」公众号后台回复：Python视觉实战项目，即可下载包括图像分割、口罩检测、车道线检测、车辆计数、添加眼线、车牌识别、字符识别、情绪检测、文本内容提取、面部识别等31个视觉实战项目，助力快速学校计算机视觉。


下载3：OpenCV实战项目20讲
在「小白学视觉」公众号后台回复：OpenCV实战项目20讲，即可下载含有20个基于OpenCV实现20个实战项目，实现OpenCV学习进阶。


交流群

欢迎加入公众号读者群一起和同行交流，目前有SLAM、三维视觉、传感器、自动驾驶、计算摄影、检测、分割、识别、医学影像、GAN、算法竞赛等微信群（以后会逐渐细分），请扫描下面微信号加群，备注：”昵称+学校/公司+研究方向“，例如：”张三 + 上海交大 + 视觉SLAM“。请按照格式备注，否则不予通过。添加成功后会根据研究方向邀请进入相关微信群。请勿在群内发送广告，否则会请出群，谢谢理解~