【python与数据分析】实验十四 北京市空气质量回归分析
目录
【代码一】
【结果一】
编辑【代码二】
【结果二】
【代码一】
#本章需导入的模块
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
##%matplotlib inline
plt.rcParams['font.sans-serif']=['SimHei'] #解决中文显示乱码问题
plt.rcParams['axes.unicode_minus']=False
import warnings
warnings.filterwarnings(action = 'ignore')
from sklearn.metrics import confusion_matrix,f1_score,roc_curve, auc, precision_recall_curve,accuracy_score
from sklearn.model_selection import train_test_split,KFold,LeaveOneOut,LeavePOut # 数据集划分方法
from sklearn.model_selection import cross_val_score,cross_validate # 计算交叉验证下的测试误差
from sklearn import preprocessing
import sklearn.linear_model as LM
from sklearn import neighbors
data=pd.read_excel('D:\个人成长\学业\课程\python\实验\题目\北京市空气质量数据.xlsx')
data=data.replace(0,np.NaN)#缺失值替换
data=data.dropna()
data=data.loc[(data['PM2.5']<=200) & (data['SO2']<=20)]#?
###以空气质量检测的部分数据为例,对PM2.5(输出变量)进行预测
###首先考虑只有一个输入变量CO的情况,建立一元线性回归模型
###建立线性回归模需引用sklearn中的linear_model
###一元回归
X=data[['CO']]
y=data['PM2.5']
modelLR=LM.LinearRegression()
###声明modelKR对象为线性模型
modelLR.fit(X,y)
###表示基于给出的x和y估计模型参数。其中,X为输入变量(矩阵形式),y为输出变量
print("一元回归模型的截距项:%f"%modelLR.intercept_)
print("一元回归模型的回归系数:",modelLR.coef_)
###线性回归模型参数的估计值存储在intercept_和coef_属性中,依次为截距项和回归系数
plt.scatter(data['CO'],data['PM2.5'],c='green',marker='.')
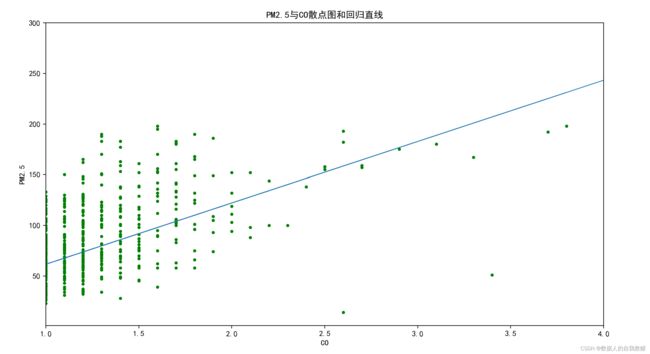
plt.title('PM2.5与CO散点图和回归直线')
plt.xlabel('CO')
plt.ylabel('PM2.5')
plt.xlim(xmax=4, xmin=1)
plt.ylim(ymax=300,ymin=1)
plt.plot(data['CO'],modelLR.predict(X),linewidth=0.8)
###modelLR.predict(X)表示将X带入回归方程计算y额预测值
plt.show()
###在研究CO对PM2.5的影响时,CO的回归系数估计值(60.59)大于0,表示其他因素不变的条件下,CO浓度增加一个单位将导致PM2.5均值增加60.59
##多元回归
X=data[['SO2','CO']]
y=data['PM2.5']
modelLR=LM.LinearRegression()
modelLR.fit(X,y)
print("多元回归模型的截距项:%f"%modelLR.intercept_)
print("多元回归模型的回归系数:",modelLR.coef_)
###在研究SO2和CO对PM2.5的影响时,CO的回归系数估计值(56.89)大于S02(0.86),表明CO对PM2.5的正向贡献大于SO2
###这里以空气质量监测数据为例,对是否有污染(二分类输出变量)进行预测
###首先对数据进行预处理,将质量等级是优和良的合并为0类(无污染),共计1204天,其余合并为1类(有污染),共计892天
###这里只考虑PM2.5和PM10对有无污染的影响,作为输入变量,只有0和1两个取值的有无污染作为输入变量,建立logistic回归模型
data=pd.read_excel('D:\个人成长\学业\课程\python\实验\题目\北京市空气质量数据.xlsx')
data=data.replace(0,np.NaN)
data=data.dropna()
data['有无污染']=data['质量等级'].map({'优':0,'良':0,'轻度污染':1,'中度污染':1,'重度污染':1,'严重污染':1})
print(data['有无污染'].value_counts())
fig = plt.figure()
ax = fig.add_subplot(111)
flag=(data['有无污染']==0)
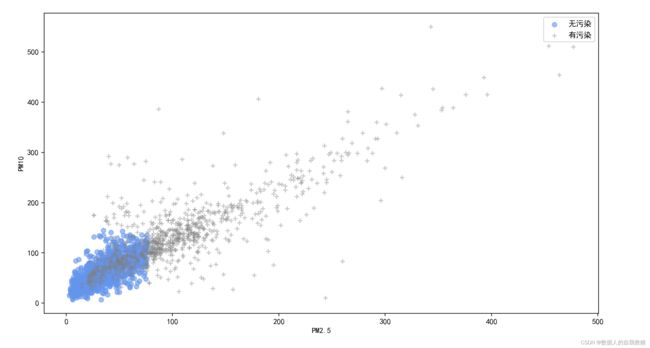
ax.scatter(data.loc[flag,'PM2.5'],data.loc[flag,'PM10'],c='cornflowerblue',marker='o',label='无污染',alpha=0.6)
flag=data['有无污染']==1
ax.scatter(data.loc[flag,'PM2.5'],data.loc[flag,'PM10'],c='grey',marker='+',label='有污染',alpha=0.4)
ax.set_xlabel('PM2.5')
ax.set_ylabel('PM10')
plt.legend()
##Logistic回归
X=data[['PM2.5','PM10']]
y=data['有无污染']
modelLR=LM.LogisticRegression()
###定义modelLR对象为Logistic回归模型
modelLR.fit(X,y)
###表示基于给出的X和y估计模型参数。其中X为输入变量(矩阵形式),y为输出变量
print("截距项:%f"%modelLR.intercept_)
print("回归系数:",modelLR.coef_)
###模型参数的估计值存储在intercept_和.coef_属性中,依次为截距项和回归系数。
###从回归系数估计值看,PM2.5(系数为0.05)对是否有污染的作用比PM10(系数0.02)更大
print("优势比{0}".format(np.exp(modelLR.coef_)))
yhat=modelLR.predict(X)
###表示将X带入回归方程计算y的预测值
print("预测结果:",yhat)
plt.show()【结果一】
 【代码二】
【代码二】
#本章需导入的模块
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
#%matplotlib inline
plt.rcParams['font.sans-serif']=['SimHei'] #解决中文显示乱码问题
plt.rcParams['axes.unicode_minus']=False
import warnings
warnings.filterwarnings(action = 'ignore')
from sklearn.metrics import confusion_matrix,f1_score,roc_curve, auc, precision_recall_curve,accuracy_score
from sklearn.model_selection import train_test_split,KFold,LeaveOneOut,LeavePOut # 数据集划分方法
from sklearn.model_selection import cross_val_score,cross_validate # 计算交叉验证下的测试误差
from sklearn import preprocessing
import sklearn.linear_model as LM
from sklearn import neighbors
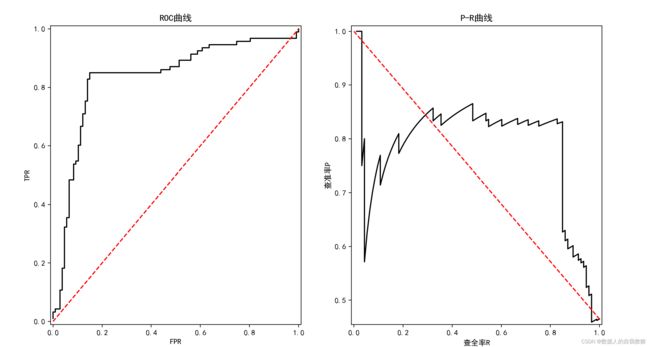
#这里给出绘制ROC曲线和P-R曲线的示例。数据来自名为“类别和概率.csv”的文本文件,包括两列数据。
#第一列为模型预测为1类的概率值,第二列为实际标签(0/1)
#首先,计算实际标签为1和0类的样本量(pos和neg)
#然后,将数据按概率值降序重新排列
data = pd.read_csv('D:\个人成长\学业\课程\python\实验\题目\类别和概率.csv')
label=data['label']
prob=data['prob']
pos = np.sum(label == 1)
neg = np.sum(label == 0)
prob_sort = np.sort(prob)[::-1]
#对prob由小到大排序,然后逆向输出
index = np.argsort(prob)[::-1]
#提取排序结果元素在排列前对应的index(索引)
label_sort = label[index]
Pre = []
Rec = []
tpr=[]
fpr=[]
#利用for循环计算绘图所需数据,FPR,TPR,查全率R和查准率P
#循环中的i为索引,item为prob_sort的具体值(预测数据)
#item值的重要应用是确定合理的概率阈值,应为TPR/FPR最大处的item值
#这里采用enumerate()函数,用于给出一个可遍历数据对象(如列表)的索引和对应的数据
for i, item in enumerate(prob_sort):
Rec.append(np.sum((label_sort[:(i+1)] == 1)) /pos)
Pre.append(np.sum((label_sort[:(i+1)] == 1))/(i+1))
tpr.append(np.sum((label_sort[:(i+1)] == 1))/pos)
fpr.append(np.sum((label_sort[:(i+1)] == 0)) /neg)
fig,axes=plt.subplots(nrows=1,ncols=2,figsize=(10,4))
axes[0].plot(fpr,tpr,'k')
axes[0].set_title('ROC曲线')
axes[0].set_xlabel('FPR')
axes[0].set_ylabel('TPR')
axes[0].plot([0, 1], [0, 1], 'r--')
axes[0].set_xlim([-0.01, 1.01])
axes[0].set_ylim([-0.01, 1.01])
axes[1].plot(Rec,Pre,'k')
axes[1].set_title('P-R曲线')
axes[1].set_xlabel('查全率R')
axes[1].set_ylabel('查准率P')
axes[1].plot([0,1],[1,pos/(pos+neg)], 'r--')
axes[1].set_xlim([-0.01, 1.01])
axes[1].set_ylim([pos/(pos+neg)-0.01, 1.01])
#这里利用空气质量监测数据,建立Logistic回归模型对是否有污染进行分类预测
#其中的输入变量包括PM2.5,PM10,SO2,CO,NO2,03污染物浓度,是否有污染为二分类的输出变量(1为有污染,0为无污染)
#进一步,对模型进行评价,设计ROC曲线,AUC值以及F1分数等
#需要引用sklearn.metrics中的confusion_matrix,f1_score,roc_curve,auc,以及import accuracy_score等
data=pd.read_excel('D:\个人成长\学业\课程\python\实验\题目\北京市空气质量数据.xlsx')
data=data.replace(0,np.NaN)
data=data.dropna()
data['有无污染']=data['质量等级'].map({'优':0,'良':0,'轻度污染':1,'中度污染':1,'重度污染':1,'严重污染':1})
data['有无污染'].value_counts()
X=data.loc[:,['PM2.5','PM10','SO2','CO','NO2','O3']]
Y=data.loc[:,'有无污染']
modelLR=LM.LogisticRegression()
modelLR.fit(X,Y)
print('训练误差:',1-modelLR.score(X,Y)) #print(accuracy_score(Y,modelLR.predict(X)))
#modelLR.score(X,Y)为预测模型的精度得分(基于训练集的)。分类预测的精度得分为总的预测正确率
#也可以通过accuracy_score函数得到同样结果
print('混淆矩阵:\n',confusion_matrix(Y,modelLR.predict(X)))
#计算模型的混淆矩阵
print('F1-score:',f1_score(Y,modelLR.predict(X),pos_label=1))
#针对1类计算F1得分
fpr,tpr,thresholds = roc_curve(Y,modelLR.predict_proba(X)[:,1],pos_label=1) ###计算fpr和tpr
#存储模型预测为0类和1类的概率,这里关心预测为1类的概率
#计算预测为1类的概率从大到小过程中的TPR和FPR
roc_auc = auc(fpr,tpr) ###计算auc的值
#计算ROC曲线下的面积
print('AUC:',roc_auc)
print('总正确率',accuracy_score(Y,modelLR.predict(X)))
fig,axes=plt.subplots(nrows=1,ncols=2,figsize=(10,4))
axes[0].plot(fpr, tpr, color='r',linewidth=2, label='ROC curve (area = %0.5f)' % roc_auc)
axes[0].plot([0, 1], [0, 1], color='navy', linewidth=2, linestyle='--')
axes[0].set_xlim([-0.01, 1.01])
axes[0].set_ylim([-0.01, 1.01])
axes[0].set_xlabel('FPR')
axes[0].set_ylabel('TPR')
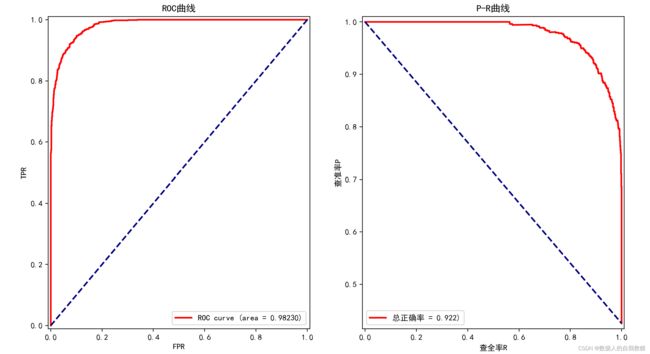
axes[0].set_title('ROC曲线')
axes[0].legend(loc="lower right")
pre, rec, thresholds = precision_recall_curve(Y,modelLR.predict_proba(X)[:,1],pos_label=1)
#计算预测为1类的概率从大到小过程中的查准率P和查全率R
axes[1].plot(rec, pre, color='r',linewidth=2, label='总正确率 = %0.3f)' % accuracy_score(Y,modelLR.predict(X)))
axes[1].plot([0,1],[1,pre.min()],color='navy', linewidth=2, linestyle='--')
axes[1].set_xlim([-0.01, 1.01])
axes[1].set_ylim([pre.min()-0.01, 1.01])
axes[1].set_xlabel('查全率R')
axes[1].set_ylabel('查准率P')
axes[1].set_title('P-R曲线')
axes[1].legend(loc='lower left')
plt.show()
#ROC曲线和AUC值,以及P-R曲线均表明,该预测模型的预测误差(训练误差)很小