【CS231N笔记】P6:可视化卷积神经网络

子豪兄YYDS
https://www.bilibili.com/video/BV1K7411W7So?p=6

一、什么是卷积神经网络的可视化

卷积神经网络可以看作一个黑箱子，打破黑箱子就需要处理中间过程。打破黑箱子之后，神经网络的结构相当于一个多层的汉堡，每一层都处理了一个特征。
对于卷积神经网络，按照上一节的内容，卷积核在不断的移动中提取输入中符合目标的特征，我们可以知道底层卷积核提取的特征是基础的特征，对于人来说比较好理解，但是层数越高，特征就越抽象，对人来说也就越来越难理解，如果我们想知道某些高层神经元是判断哪个特征，就需要采用可视化的方法，从而更加方便人去理解神经网络中的每一层。

二、小图片段

利用小图片段，看能够使指定神经元激活值最大的小图片是什么，从而推断某些神经元对什么内容比较敏感。

小图片指的是数据集中每张图片的截取片段，将这些小图片送入神经网络，看看哪些神经元会对这些小图片表示出比较大的激活值。

从这张图来看，一些神经元对第一行的数据给出了很大的激活值，而人可以理解第一行的数据都是人的图片，所以这些给出很大激活值的神经元是对人这个输入比较敏感的神经元。同理倒数第一行都是一些球体的反光，所以对这些图片激活值比较大的神经元，就是对球体反射比较敏感的神经元。

三、可视化卷积核

可视化卷积核的部分在课程里提到的不多，个人的理解就是描述了通道的性质，筛选特征如果看做使用一个漏斗，那么可视化卷积核就是将这个漏斗的漏嘴的形状给描述了出来，反正要筛选的是特征，那么图片上的特征和筛选的标准必然是一一对应的，那么可视化特征标准一定程度上也可以反应神经网络的信息。

这张图是可视化了卷积核，可以看见下面的那部分带颜色的方格，这部分是筛选RGB三个通道的卷积核，卷积核的某个颜色的值比较高，对应在输入的图上要筛选的部分颜色也比较高，所以一定程度上也可以反应卷积神经网络的筛选情况。

四、可视化经过全连接层后的编码

编码指的是经过卷积和池化之后，得到的多个特征图在送入全连接层的时候会拉成一个长向量，这个长向量就可以看做是一个编码。将这个长向量降维到人可以感知的维度，就可以进行可视化的任务。

这张图就是一个可视化后的结果，首先将训练集放到神经网络里面，经过卷积层和池化层处理，在送入全连接层之前得到多个长向量，一个长向量对应一个训练数据。利用这些长向量，降维到二维，然后放入二维坐标系，结合数据的类别，可以得到这张可视化的图，可以看见整个数据集已经被分开了。

五、遮挡实验

遮挡实验真的是遮挡，每次都遮挡实验数据中的一部分，看输出结果会产生什么样的变化。这一点就很像高中物理的控制变量法，每次改变一部分看剩下的部分会产生什么样的变化。

这张图展示了遮挡实验的结果，在一开始的输入上增加一个遮挡物来遮挡输入的一部分，看反应在后面的高层神经元产生的特征图会产生什么样的变化，从而得知某个神经元对哪个特征敏感。

六、反卷积和导向反向传播

首先明确一下，这两个方法的目的都是用于反向传回，就是利用某个神经元，反向传回输入层，看输入层的哪部分对这个神经元的激活起了作用。它们的目的都是求得指定神经元的激活值相对于输入图像每个像素的梯度。也就是在求输入图像的像素该怎么变化才可以使中间的某个神经元发生最合适的变化。
这里可以看作提前结束的反向传播。正常情况的反向传播都是以损失函数为起点，看神经网络每个参数对损失函数的梯度，也就是每个参数怎样变化会影响损失函数。而这里也是一个道理，只不过起点换成了中间的某个神经元。

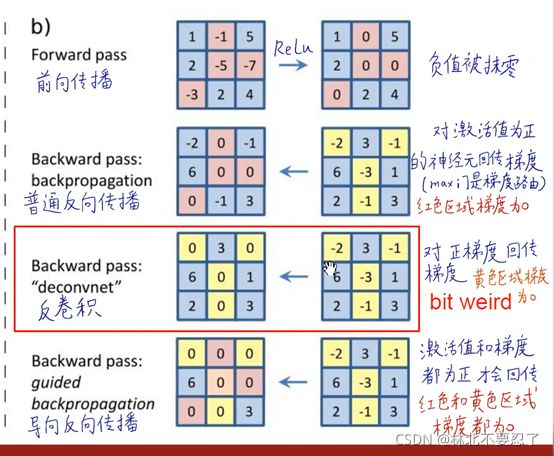
这张图展示的就是一个反向传播的演示，反向传播主要有三种方式，主要的区别在于对传回的限制。
首先在前向传播的时候，采用的激活函数是ReLU函数，那么前向传播的结果是让负数的输入变成0，而整数的输入则保持不变直接输出。

对于普通反向传播，由于前向时的激活函数是ReLU，所以反向传播时，对于正的输入值才回传梯度，其余情况则不回传梯度。这里可以这样去理解，对于上图中的输入，假设第一行第二列的-1是w，那么如果要求后面某个神经元对w的梯度，那么按照反向传播的思想，需要利用链式求导法则不断做乘法，但是到了这一步，由于普通反向传播的规则，这里反向传回时乘以局部梯度，但是局部梯度时0，所以反向传回的是0，全局梯度直接变成0，也就是对后面的神经元没有影响。其实这里也可以结合ReLU的图像去理解，ReLU在x小于0的部分导数都为0，所以求梯度自然是0，不管输入是负几，输出都是0，自然就不会对后续的神经网络产生影响，在反向传播的时候必然也是0，这里正好对上了前面提到的梯度丢失问题。

反卷积和普通反向传播的思路其实差不多，反卷积要求只有正梯度才可以反向传回，否则传回0。

在百度上查反卷积，基本都是卷积的反向操作，卷积会让图片的尺寸变小，而反卷积可以看作卷积的反操作。

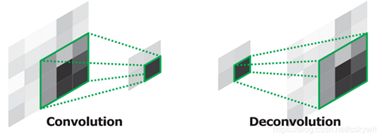
对于反卷积，首先要从卷积开始看，根据卷积的定义，我们相当于做了很多个矩阵的乘法，每个乘法都是输入的感受野与卷积核对应位置相乘再相加，将结果拼成一个矩阵，这个操作的过程可以等效为一个矩阵的乘法，输入矩阵与一个特殊设计的矩阵相乘，结果刚好是卷积运算的结果，反正输入输出都是矩阵，只要设计的矩阵合适就可以实现这个等效，这样卷积运算可以写成Y=CX，Y表示卷积结果，C表示设计的矩阵，X表示输入矩阵，那么前向传播就等效与和矩阵C相乘，反向传播就是和矩阵C的转置相乘。从直观上看，卷积使特征图宽和高变小进行更进一步的特征提取和抽象，反卷积是反向还原特征图大小的过程。

回到之前反向传播的反卷积，这里的反卷积要求梯度大于0才反向传回梯度值，而其余情况只传回一个0，个人感觉这里的反卷积和扩大用的反卷积有联系但又不像是一个东西。

关于反向传播，反卷积和普通反向传播分别是两个角度来处理relu函数，对于普通反向传播，输入值大于0才会经过relu函数而不变成0，这种情况下求局部梯度的时候才会变成1，所以反向传播的时候这里相当于乘了1，所以成功返回到上一层，而输入值小于0，经过relu函数变成0，梯度也是0，在反向传播的时候乘以0变成了零，返回到上一层的梯度就是0。
而反卷积是从结果来看的，梯度为正，表示沿着变量增加的方向移动会让因变量的结果也增加，那么从这里来看，如果梯度为负数，此时增加上一层的输入反而会抑制最终神经元的激活，这正好与我们的目标相反，如果这样的情况返回到输入层，那就意味着某个位置的输入对最终神经元的激活是没有意义的，也就是对判断没有意义，可以看作是无关紧要的点，直接不用考虑。所以反卷积实际上是限制了小于0的梯度的回传，而梯度小于0的部分对应了原图中削弱了我们想要可视化的特征 的部分，这些部分正是我们不想要的。

导向反向传播则是反卷积和普通反向传播的结合，只允许输入和梯度都大于0的梯度反向传回，是一个优中选优的过程。采用这种方法，不仅限制了对神经元起抑制作用的梯度的回传，还消除了不产生影响的梯度，这会让很多梯度回传变成0，相当于在计算后面神经元对输入像素值的梯度时，很多梯度都变成了0，只有最直接最优秀的才留了下来，从而让可视化的效果更加的清楚。
利用这两种方式的结合，导向反向传播实现了判断内容的筛选。因为神经网络内部是黑箱，我们拆开后一开始的层还能看懂，但是到了深层，特征已经很抽象了，人已经看不出是哪一个特征了，所以这个时候利用反向传播，从某个神经元开始，利用链式规则反向传播到输入层，得到一个反向生成的图，这个图里的点都是对当前神经元激活起作用的点，也就是判断的依据。

这个图就是可视化的结果，这个可视化是反向生成的，因为人很难理解神经网络中比较靠后的部分的结果，所以利用前面的导向反向传播，先在前向传播的过程中，截取一个神经元的输出，通过假设梯度，利用导向反向传播，逆推回输入空间，这样就可以得到目前神经元提取的特征是一开始输入的哪一部分。从这个角度看的话，反卷积就是一个恢复特征的过程，卷积是在压缩，而反向推回输入空间时，需要的就是恢复，因此才引入了反卷积操作。

将这个反向逆推的起点向后移动，移动到输出的位置，那么就变成了输出某个类别对输入的梯度，可视化这个梯度，可以看作原图中哪个部分对判断这个类别起到了重要的作用。

对这个图来说，判断第二张图是狗，那么最关键的是狗的特征，而不是背景中沙滩的信息，采用可视化梯度可以看见，狗所在位置的轮廓很明显，正好对应判断类别的过程。

除了可视化梯度，还可以可视化原图，也是利用同样的思路，取一个梯度为1剩下的为0，反向传回原图并且进行可视化，得到的就是判断这个类别的证据。