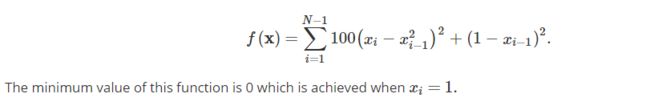python中的优化函数

这篇博客对python中的scipy.optimize.minimize常用方法进行总结：
https://blog.csdn.net/jiang425776024/article/details/87885969
官方文档：
https://docs.scipy.org/doc/scipy-0.18.1/reference/tutorial/optimize.html#constrained-minimization-of-multivariate-scalar-functions-minimize

scipy.optimize.minimize()的用法

参考官方文档：
https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.minimize.html

函数形式：

scipy.optimize.minimize(fun, x0, args=(), method=None, jac=None, hess=None, hessp=None, bounds=None, constraints=(), tol=None, callback=None, options=None)

参数介绍：

• fun:目标函数, fun(x,*args)->float, x是一个一维数值shape(n,), args是一个tuple.

• x0:初值。ndarray,shape(n,)

• args:参数，tuple

• method:优化方法，可选。如果缺失，将从 BFGS, L-BFGS-B, SLSQP中选择一个，根据这个问题是否有约束来决定。一般对于有约束的问题，常用SLSQP方法。可选的方法有：
  ‘Nelder-Mead’

  ‘Powell’

  ‘CG’

  ‘BFGS’

  ‘Newton-CG’

  ‘L-BFGS-B’

  ‘TNC’

  ‘COBYLA’

  ‘SLSQP’

  ‘trust-constr’

  ‘dogleg’

  ‘trust-ncg’

  ‘trust-exact’

  ‘trust-krylov’

  custom - a callable object (added in version 0.14.0), see below for
  description.

  • jac:雅可比矩阵，可选参考。但是对于这些方法： CG, BFGS, Newton-CG, L-BFGS-B, TNC, SLSQP, dogleg, trust-ncg, trust-krylov, trust-exact and trust-constr，是需要的。jac(x, *args) -> array_like, shape (n,)
  • hess:hessian矩阵，可选。但是对于 Newton-CG, dogleg, trust-ncg, trust-krylov, trust-exact and trust-constr，是必须的。hess(x, *args) -> {LinearOperator, spmatrix, array}, (n, n)
  • hessp:hessian*p矩阵，可选。但对于：Newton-CG, trust-ncg, trust-krylov, trust-constr，是需要的。如果有hessian矩阵可以不要这个，两个是等价的。hessp(x, p, *args) -> ndarray shape (n,)
  • bounds:x的取值范围，可选。是一个（min,max）的序列。
  • constraints:约束条件，字典类型，或者是字典的list。每个字典的包含：1.type:str, ‘eq’ for equality; ‘ineq’ for inequality.2.fun:callalbe,约束函数，如果是不等式需要保证》；3.jac:雅可比矩阵，可选，only for SLSQP；4.args: 约束中的参数。
  • tol:float,optional,优化精度。
  • options:dict,optional.包含：1.maxiter:int, 最大循环次数；2.disp:bool,是否打印收敛信息。
  • callback:callable,optional。

一个无约束的优化问题例子：

目标函数：

import numpy as np
from scipy.optimize import minimize

def rosen(x):
    """The Rosenbrock function"""
    return sum(100.0*(x[1:]-x[:-1]**2.0)**2.0 + (1-x[:-1])**2.0)

雅可比矩阵

def rosen_der(x):
    #jacbion矩阵（导数矩阵）
    #注意返回值是个数组!!!!而且尺寸要和初值x0一致
    xm = x[1:-1]
    xm_m1 = x[:-2]
    xm_p1 = x[2:]
    der = np.zeros_like(x)
    der[1:-1] = 200*(xm-xm_m1**2) - 400*(xm_p1 - xm**2)*xm - 2*(1-xm)
    der[0] = -400*x[0]*(x[1]-x[0]**2) - 2*(1-x[0])
    der[-1] = 200*(x[-1]-x[-2]**2)
    return der

hessian矩阵

def rosen_hess(x):
    #hessian矩阵
    #返回对象是个二维数组
    x = np.asarray(x)
    H = np.diag(-400*x[:-1],1) - np.diag(400*x[:-1],-1)
    diagonal = np.zeros_like(x)
    diagonal[0] = 1200*x[0]**2-400*x[1]+2
    diagonal[-1] = 200
    diagonal[1:-1] = 202 + 1200*x[1:-1]**2 - 400*x[2:]
    H = H + np.diag(diagonal)
    return H

H*p矩阵

def rosen_hess_p(x, p):
    #H*p的矩阵
    #返回对象是个一维数组
    x = np.asarray(x)
    Hp = np.zeros_like(x)
    Hp[0] = (1200*x[0]**2 - 400*x[1] + 2)*p[0] - 400*x[0]*p[1]
    Hp[1:-1] = -400*x[:-2]*p[:-2]+(202+1200*x[1:-1]**2-400*x[2:])*p[1:-1] \
               -400*x[1:-1]*p[2:]
    Hp[-1] = -400*x[-2]*p[-2] + 200*p[-1]
    return Hp

求解

method=‘nelder-mead’(Nelder-Mead Simplex algorithm)

x0 = np.array([1.3, 0.7, 0.8, 1.9, 1.2])

res = minimize(rosen, x0, method='nelder-mead',
               options={'xtol': 1e-8, 'disp': True})
res.x

method=‘BFGS’(Broyden-Fletcher-Goldfarb-Shanno algorithm)

该方法需要提供jacbian矩阵

res = minimize(rosen, x0, method='BFGS', jac=rosen_der,
               options={'disp': True})
res.x

method=‘Newton-CG’(Newton-Conjugate-Gradient algorithm)

该方法需要提供hessian矩阵或者H*p矩阵

res = minimize(rosen, x0, method='Newton-CG',
               jac=rosen_der, hess=rosen_hess,
               options={'xtol': 1e-8, 'disp': True})
res.x

或者

res = minimize(rosen, x0, method='Newton-CG',
               jac=rosen_der, hessp=rosen_hess_p,
               options={'xtol': 1e-8, 'disp': True})
res.x

加入约束再求解：

bnds = [(-1, 1), (0, 1), (1, 2), (2, 3), (2,3)]
cons = [{'type': 'ineq',
         'fun': lambda x: 20 - np.max(x)},
        {'type': 'ineq',
         'fun': lambda x: x[0] ** 2 - 1},
        {'type': 'eq',
         'fun': lambda x: sum(x) - 8}]


x0 = np.array([1.5, 10, 2, 1,1])

res = minimize(rosen, x0, method='SLSQP', jac=rosen_der, hess=rosen_hess, constraints=cons,tol=1e-8,options={'maxiter': 100, 'disp': True})
res.x
#array([1.06715431, 1.13836014, 1.29554771, 1.67882844, 2.8201094 ])

加入约束条件后的一个坑，必看

bnds = [(-1, 1), (0, 1), (1, 2), (2, 3), (2,3)]
#对于无约束的可以利用np.inf表示无穷大
cons = [{'type': 'ineq',
         'fun': lambda x: 20 - np.max(x)},
        {'type': 'ineq',
         'fun': lambda x: x[0] ** 2 - 1,
         'jac': lambda x: np.array([1, 0, 0, 0, 0])},
        {'type': 'eq',
         'fun': lambda x: sum(x) - 8,
         'jac': lambda x: np.array([1, 1, 1, 1, 1])}]



x0 = np.array([1.5, 10, 2, 1,1])

res = minimize(rosen, x0, method='SLSQP', jac=rosen_der, hess=rosen_hess, constraints=cons,tol=1e-8,options={'maxiter': 100, 'disp': True})
res.x
#array([-1.09048374,  1.19989405,  1.44400407,  2.08729029,  4.35929534])
#可以看到这里有几个x已经超出了x的约束！！！！！
#因此，简单约束的时候jac给还不如不给

一个一元有约束的例子：

问题形式：

求解：

def func(x, sign=1.0):
    """ Objective function """
    return sign*(2*x[0]*x[1] + 2*x[0] - x[0]**2 - 2*x[1]**2)


def func_deriv(x, sign=1.0):
    """ Derivative of objective function """
    dfdx0 = sign*(-2*x[0] + 2*x[1] + 2)
    dfdx1 = sign*(2*x[0] - 4*x[1])
    return np.array([ dfdx0, dfdx1 ])

cons = ({'type': 'eq',
         'fun' : lambda x: np.array([x[0]**3 - x[1]]),
         'jac' : lambda x: np.array([3.0*(x[0]**2.0), -1.0])},
        {'type': 'ineq',
         'fun' : lambda x: np.array([x[1] - 1]),
         'jac' : lambda x: np.array([0.0, 1.0])})


res = minimize(func, [-1.0,1.0], args=(-1.0,), jac=func_deriv,
               method='SLSQP', options={'disp': True})

print(res.x)

使用scipy.optimize.minimize()时遇到的问题

问题1：IndexError: too many indices for array
答：在网上查阅了一圈后，发现造成这个问题的原因有很多。而我是由于用scipy.optimize.minimize()做优化时，传入的参数x0 = theta的shape为矩阵，而官方要求是向量的形式！（哎，太粗心啦）

问题2：ValueError: shapes (2,2) and (1,2) not aligned: 2 (dim 1) != 1 (dim 0)
答：这个问题是在问题1解决之后产生的新问题！疯狂的打印信息后，发现：如果用scipy.optimize.minimize()做优化，梯度函数gradient返回值必须是1维数组的形式，即（n,）。因为梯度的shape必须和参数theta的shape一致。

参考：https://blog.csdn.net/TianJingDeng/article/details/103796772