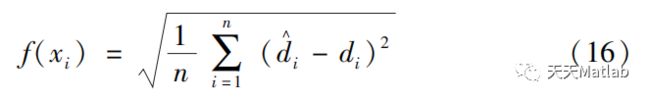【KELM预测】基于麻雀算法优化核极限学习机实现数据回归预测附matlab代码

✅作者简介：热爱科研的Matlab仿真开发者，修心和技术同步精进，matlab项目合作可私信。

个人主页：Matlab科研工作室

个人信条：格物致知。

更多Matlab仿真内容点击

智能优化算法  神经网络预测 雷达通信  无线传感器

信号处理 图像处理 路径规划 元胞自动机 无人机  电力系统

⛄ 内容介绍

极限学习机(Extreme Learning Machine, ELM)是近几年发展起来的一种有效的新型单隐层前馈神经网络学习算法,和传统学习算法不同的是,ELM算法的网络参数随机选取,无需调节,输出权值是通过对平方损失函数最小化得到的最小二乘解,因此该算法具有较快的学习速度和良好的泛化性能,并在多模式分类,非线性预测等领域得到了广泛的应用.但是ELM在学习过程中也不可避免的存在众多缺点,其参数的随机选取导致一系列非最优参数的生成,使得所需隐含层节点数多于传统学习算法,影响其泛化性能,并导致系统的病态;在学习过程中仅仅只利用了输入参数的信息进行计算,而忽略了非常有价值的实际输出值;将其应用于工业生产中所得到的精度不能满足实际的标准等等.针对上述缺点,本文提出了一种对ELM的麻雀搜索算法极限学习机(SSA-ELM)。

1 麻雀搜索算法原理

麻雀搜索算法是一种新型的群智能优化算法， 在 2020 年由 Xue 等 [15] 提出，主要是受麻雀的觅食 和反哺食行为启发，具有寻优能力强、收敛速度快的特点。麻雀搜索算法将整个麻雀种群分为三类，即寻找食物的生产者，抢夺食物的加入者和发现危险的警戒者 。生产者和加入者可以相互转化，但各自在 种群中的占比不会发生变化。在模拟实验中，需要使用虚拟麻雀进行食物的 寻找，与其他寻优算法相同，麻雀搜索算法首先需要对麻雀种群与适应度值进行初始化，麻雀种群可 初始化为如下形式，表达式为式(3) 

中：n为麻雀的数量；d为要优化的变量的维度即独立参数的数目；xnd为第n只麻雀第d维度的值。由此，总体麻雀适应度值表征形式为 

式(4)中：f(x)为个体适应度值。适应度值较好的麻雀(即生产者)在搜索中会优先获得食物并指引群体的觅食方向与范围，与此同时，生产者会具有更大的觅食搜索范围。生产者在觅食过程中，位置不断发生移动，而在遇到捕食者时，移动规则又会发生改变，即 

式(5)中：t为当前迭代次数；j∈{1，2，…，d}；xit，j为迭代第t次时，第i个麻雀的第j个维度的值；α∈(0，1]，为随机数；iter_max为迭代次数最多的常数；R2∈[0，1]，为报警值；ST∈[0，1]，为安全阈值；Q为服从正态分布的随机数；L为1×d阶矩阵(元素全为1)。R2＜ST时，代表该区域安全，无捕食者出没，生产者会出现大范围觅食行为；R2≥ST时，表示一些麻雀发现了捕食者并发出警告，所有麻雀迅速飞入安全区域。而对加入者而言，在觅食过程中，一旦生产者找到了好的食物源，加入者必会知晓，并飞向它的附近抢食，同时，也有加入者会时刻监视生产者，随时准备争抢食物。由此加入者的位置更新规则为

式(6)中：xp为生产者占据的最佳位置；xworst为全局最差位置；A为1×d阶矩阵，每个元素随机为1或－1；A†＝AT(AAT)－1。当i＞时，表示适应性较差的第i个加入者抢夺食物失败，为了更好地获得食物避免挨饿只能飞往其他地区进行觅食。总体而言，假设意识到危险的麻雀(即警戒者)占10％~20％。初始位置则随机产生，规则为

式(7)中：λ为步长控制函数，是一个均值为0，方差为1的正态分布随机数；fi为当前麻雀适应值；fg为全局最好适应值；fw为全局最差适应值；k为麻雀移动方向；xbest为全局最优位置；ε为最小常数，避免除数为零。当fi＞fg时，警戒者位于种群边缘，意识到危险后向中央安全区靠近；当fi＝fg时，则是处于种群中央的麻雀意识到了危险，为躲避危险，则向其他麻雀身边靠拢。

2 极限学习机

传统的单隐层神经网络由三部分组成，分别是输入层、隐含层和输出层，输入层神经元节点个数即输入变量的个数，隐含层节点个数则需要人为给定，输出层节点个数也就是输出变量的个数。在2006年，新加坡南洋理工大学的Huang等[16]在传统的单隐层神经网络的基础上提出了一种新的前馈神经网络学习算法，命名为极限学习机(extremelearningmachine，ELM)，不同于传统的基于梯度的前馈神经网络算法，该方法随机产生隐含层与输入层之间的连接权值及隐含层神经元的阈值，训练过程中只需要设置隐含神经元的个数便可获得唯一最优解，极限学习机网络结构如图1所示。

3 麻雀算法优化极限学习机

本文采用麻雀搜索算法对其隐含层的初始权值与阈值进行优化，具体构建过程可以概述为:确定ELM的输入与输出样本集;确定对ELM初始权值及阈值的编码方式;随机采样产生第一代种群;计算每个个体的适应值，并排序选优;按照既定规则更新产生下一代种群直至满足终止条件为止，终止条件设置为预测值与期望值的误差矩阵的范数小于某一设定值。

利用麻雀搜索算法对核极限学习机的两项参数:核参数及正则化系数进行优化,得到耦合滑坡预测模型,其实施步骤如下。

步骤1初始化种群。设置麻雀数量为20,随机产生初始核参数及正则化系数,生成种群初始位置。

步骤2确定优化参数的取值范围。根据多次实验,确定核参数为（-100 100）,正则化系数为（-100 100）。

步骤3建立SSA-KELM耦合模型,计算麻雀个体适应度,对适应度值进行排序,寻找出当前最好和最差的个体。

适应度函数为式(16)中为真实值;为函数预测值。

步骤4根据式式(7)更新麻雀位置。

步骤5获取新的麻雀位置及个体适应度值,将本轮最优适应度值与之前的最优适应度值做比较,如果本轮更优,则更新全局最优适应度值与相关位数。

步骤6循环结束。当迭代次数大于500,则寻优过程结束。步骤7得到KELM的最佳训练参数,模型建立。

⛄ 部分代码

%KELM （分类）训练函数

%输入：P_train训练输入数据

%      T_train训练数据对应的类别标签

%      Regularization_coefficient：正则化系数C

%      Kernel_type 核类型                - Type of Kernels:

%                                   'RBF_kernel' for RBF Kernel

%                                   'lin_kernel' for Linear Kernel

%                                   'poly_kernel' for Polynomial Kernel

%                                   'wav_kernel' for Wavelet Kernel

%

%       Kernel_para 核参数[0.1,10]

%输出： TrainOutT，训练以后，得到得预测标签值

%       OutputWeight，训练得到得权重

function [TrainOutT,OutputWeight] = kelmTrain(P_train,T_train,Regularization_coefficient,Kernel_type,Kernel_para)

         % 预测标签值  训练得到的权重           P 输入矩阵  T 训练数据对应的类别标签   正则化系数          核类型       核参数                                 

%%%%%%%%%%% Training Phase %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

P = P_train;

n = length(T_train);

C = Regularization_coefficient;

[maxClass] = max(T_train);

T = T_train;

Omega_train = kernel_matrix(P',Kernel_type, Kernel_para);

OutputWeight=((Omega_train+speye(n)/C)\(T'));

Y=(Omega_train * OutputWeight)';

TrainOutT = Y;

end

⛄ 运行结果

⛄ 参考文献

[1]马飞燕, 李向新. 基于改进麻雀搜索算法-核极限学习机耦合算法的滑坡位移预测模型[J]. 科学技术与工程, 2022(022-005).

❤️ 关注我领取海量matlab电子书和数学建模资料

❤️部分理论引用网络文献，若有侵权联系博主删除