【数学建模之Python】8.解决画散点图时由于标签非常多导致的重叠现象（利用adjustText库解决）

你们的每个赞都能让我开心好几天✿✿ヽ(°▽°)ノ✿

目录

一、现象陈述

二、、adjustText的了解

1.官方文档

2.参考资料，写的相当好！以下第一个实例就是根据他写的，但我做了进一步的简化与重点提炼

3.用法

4.举例

5.代码

三、改善自我的程序

1.题目

2.代码

3.效果

---

一、现象陈述

当我们在做可视化时，例如画x-y散点图时，往往需要给散点图上的点标上标签，但是当散点图过多、过于稠密时，matplotlib.pyplot就无法满足让标签清晰的需求了。因此，以下采用adjustText解决该问题

版本声明

Python  3.7.1

adjustText   0.7.3

二、adjustText的了解

1.官方文档

2.参考资料，写的相当好！以下第一个实例就是根据他写的，但我做了进一步的简化与重点提炼

3.用法

adjustText.adjust_text(texts,x=None,y=None,add_objects=None,ax=None,expand_text=(1.05,1.2),expand_points=(1.05,1.2),expand_objects=(1.05,1.2),expand_align=(1.05,1.2),autoalign='xy',va='center',ha='center',force_text=(0.1,0.25),force_points=(0.2,0.5),force_objects=(0.1,0.25),lim=500,precision=0.01,only_move={'objects': 'xy','points': 'xy','text':'xy'},avoid_text=True,avoid_points=True,avoid_self=True,save_steps=False,save_prefix='',save_format='png',add_step_numbers=True,*args,**kwargs)

adjustText中的核心功能都通过调用函数adjust_text来实现，其核心参数如下：

texts：List型，每个元素都是表示单个文字标签对应的matplotlib.text.Text对象

ax：绘制文字标签的目标axe对象，默认为最近一次的axe对象

lim：int型，控制迭代调整文本标签位置的次数，默认为500次

precision：float型，用于决定迭代停止的精度，默认为0.01，即所有标签相互遮挡部分的长和宽占所有标签自身长宽之和的比例，addjust_text会在精度达到precision和迭代次数超过lim这两个条件中至少有一个满足时停止迭代

only_move：字典型，用于指定文本标签与不同对象发生遮挡时的位移策略，键有'points'、'text'和'objects'，对应的值可选'xy'、'x'、'y'，分别代表竖直和水平方向均调整、只调整水平方向以及只调整竖直方向

arrowprops：字典型，用于设置偏移后的文字标签与原始位置之间的连线样式，下文会作具体演示

save_steps：bool型，用于决定是否保存记录迭代过程中各轮的帧图像，默认为False

save_prefix：str型，当save_steps设置为True时，用于指定中间帧保存的路径，默认为''，即当前工作路径

这个库要自己下，在Anaconda Prompt里pip install adjustText即可

4.举例

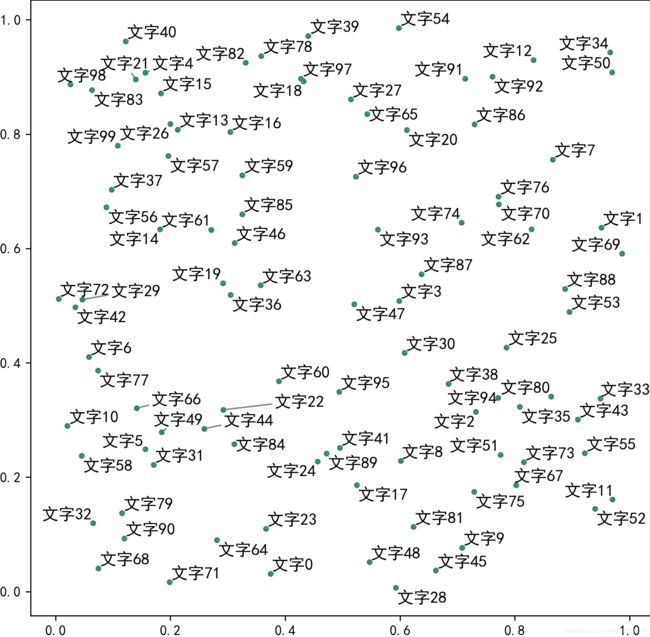
（1）简单说明：里面有100个点，100个标签，如果直接画的话，会是这样：

这样可视化看起来非常糟糕，相邻的点的标签重叠在了一起，根本分不清谁是谁！ 

（2）使用adjust_text之后：

是不是美观了许多？没有重叠的现象了，但是好像线条不是很好看

（3）再进一步修改！

又有整洁度又有线条，很好看，能够非常清晰的表现出标签的指明对象了

5.代码

import matplotlib.pyplot as plt
from adjustText import adjust_text
import numpy as np

#解决中文显示问题
plt.rcParams['font.sans-serif'] = ['SimHei']
seed = np.random.RandomState(42) # 固定随机数水平
x, y = seed.uniform(0, 1, [2, 100]) # 产生固定的均匀分布随机数
texts = [f'文字{i}' for i in range(x.__len__())]

#一、
fig, ax = plt.subplots(figsize=(8, 8))
ax.scatter(x, y, c='SeaGreen', s=10) # 绘制散点
# 绘制所有点对应的文字标签
for x_, y_, text in zip(x, y, texts):
    plt.text(x_, y_, text, fontsize=12)
fig.savefig('原图.png', dpi=300, bbox_inches='tight', pad_inches=0) # 保存图像

#二、
fig, ax = plt.subplots(figsize=(8, 8))
ax.scatter(x, y, c='SeaGreen', s=10) # 绘制散点
# 使用adjustText修正文字重叠现象
new_texts = [plt.text(x_, y_, text, fontsize=12) for x_, y_, text in zip(x, y, texts)]
#print(new_texts)了解new_texts是什么类型的
adjust_text(new_texts,only_move={'text': 'x'},arrowprops=dict(arrowstyle='-', color='grey'))
fig.savefig('使用adjust_text调整后的图.png', dpi=300, bbox_inches='tight', pad_inches=0) # 保存图像

#三、
fig, ax = plt.subplots(figsize=(8, 8))
ax.scatter(x, y, c='SeaGreen', s=10) # 绘制散点
# 使用adjustText修正文字重叠现象
new_texts = [plt.text(x_, y_, text, fontsize=12) for x_, y_, text in zip(x, y, texts)]
adjust_text(new_texts,arrowprops=dict(arrowstyle='->',color='red',lw=1))
fig.savefig('修改线型与颜色后的图.png', dpi=300, bbox_inches='tight', pad_inches=0)
plt.show()

（5）注意事项：

要想移植该程序，要明白new_texts的类型是什么！如下图所示

 其次，这个程序运行的时间会久一些，因为采用的算法是迭代多次

三、改善自我的程序

这个问题是在我做数学建模时遇到的，以下是我解决该案例的方法，如果大家不做这个的话可以不用看了，看上面的例题即可。

1.题目

某高校数学系为开展研究生的推荐免试工作，对报名参加推荐的52名学生已修过的6门课的考试分数统计如下表，这6门课的前三门是采用闭卷考试，后三门为开卷考试。我们需要对学生的考试成绩进行合理的排序，得到推荐免试的人选

（《Python数学实验与建模》司守奎例11.3.2）

学生序号	数学分析	高等代数	概率论	微分几何	抽象代数	数值分析
A1	62	71	64	75	70	68
A2	52	65	57	67	60	58
A3	51	63	55	97	78	77
A4	68	77	85	83	74	57
A5	64	70	55	76	69	62
A6	84	81	79	72	59	50
A7	65	67	57	49	61	51
A8	62	73	64	77	60	50
A9	75	94	80	67	63	45
A10	92	92	88	61	65	54
A11	41	67	50	79	75	81
A12	58	66	56	53	61	68
A13	70	65	76	100	82	69
A14	74	81	76	100	79	68
A15	71	85	77	83	56	54
A16	73	85	80	79	73	73
A17	78	74	76	60	54	41
A18	68	66	60	80	69	73
A19	82	77	73	81	53	61
A20	78	76	82	67	56	37
A21	60	70	63	75	76	54
A22	84	89	86	70	62	69
A23	100	99	95	49	58	50
A24	62	71	66	97	82	60
A25	87	87	77	92	78	63
A26	85	82	80	61	50	39
A27	59	72	66	78	82	63
A28	72	76	74	64	58	64
A29	58	66	66	83	72	79
A30	73	75	70	80	69	72
A31	68	74	60	65	61	68
A32	83	92	79	77	65	55
A33	58	60	59	91	82	68
A34	63	76	66	95	77	74
A35	65	73	73	69	71	59
A36	83	77	73	45	64	47
A37	61	80	69	84	67	60
A38	63	77	73	81	75	58
A39	63	60	70	73	68	50
A40	49	71	66	85	80	81
A41	53	63	60	99	89	81
A42	75	80	78	64	66	65
A43	76	80	79	73	65	73
A44	100	96	100	65	47	50
A45	88	91	86	75	65	60
A46	68	78	64	87	79	79
A47	87	87	83	70	62	60
A48	68	74	80	60	63	52
A49	74	82	74	56	65	59
A50	89	82	73	79	63	59
A51	75	74	66	52	70	55
A52	70	73	70	88	79	69

具体解题过程就不叙述了，重点谈谈标签修正后的效果

2.代码

import numpy as np
import pandas as pd
from sklearn import decomposition as dc
from scipy.stats import zscore
import matplotlib.pyplot as plt
from adjustText import  adjust_text
c=pd.read_excel('52名学生的原始考试成绩.xlsx',usecols=np.arange(1,7))
c=c.values.astype(float)#然后我发现第一行汉字没了
print('52名学生的原始考试成绩:\n',c)
d=zscore(c)#d是标准化后的c
r=np.corrcoef(d.T)
f=pd.ExcelWriter('例11.3.2相关系数矩阵.xlsx')
pd.DataFrame(r).to_excel(f)
f.save()

val,vec=np.linalg.eig(r)
index=np.argsort(val)[::-1]#特征值降序下标
val=np.sort(val)[::-1].round(4)#降序的特征值
vec=vec[:,index].round(4)#降序特征值对应的特征向量
cs=np.cumsum(val).round(4)#累加和，可以根据这个算出累计贡献率
print('\n特征值为val=',val,'\n累加和cs=',cs)
print('前两个因子贡献率：{}>0.8，故公共因子个数选择2个'.format(cs[1]/cs[5]))
fa=dc.FactorAnalysis(n_components=2)#取公共因子个数为2，因为前两个方差贡献率超过0.8
fa.fit(d)#求解最大方差的模型，这步必须要有，不然会报错，传入参数为标准化后的原始数据矩阵
print('\n载荷矩阵为：\n',fa.components_.T.round(4))#要转置，有6个标准化指标变量
print('\n特殊方差为：\n',fa.noise_variance_.round(4))
dd=fa.fit_transform(d).round(4)#计算因子得分
print('\n因子得分：\n',dd)

w=val[:2]/sum(val[:2])#计算两个因子的权重
df=(dd@w).round(4)#计算每个评价对象的因子总分
tf=np.sum(c,axis=1)#列向量压缩，计算每个评价对象的成绩总分

#构造pandas数据框，第1列到第5列数据分别为因子1得分、因子2得分、因子总分、成绩总分
pdf=pd.DataFrame(np.c_[dd,df,tf,np.arange(1,53).astype(int)],
                 columns=['闭卷科因子得分','开卷科因子得分','因子总分','成绩总分','学号'])

f=pd.ExcelWriter('学生的综合评价.xlsx')
pdf.to_excel(f,'sheet1')
spdf1=pdf.sort_values(by='因子总分',ascending=False)#因子总分从高到低
spdf1.to_excel(f,'sheet2')
spdf2=pdf.sort_values(by='成绩总分',ascending=False)#成绩总分从高到低
spdf2.to_excel(f,'sheet3')
print('以因子综合得分排序结果为：\n',spdf1,'\n','\n以成绩总分排序结果为：\n',spdf2)
f.save()

texts=['学号'+str(i) for i in range(1,53)]
#print(texts)
plt.rc('font',family='SimHei')
plt.rc('axes',unicode_minus=False)
fig, ax = plt.subplots()
ax.scatter(dd[:,0], dd[:,1], c='blue', s=20)#绘制散点，参数：前两个是x,y，第三个是颜色，第四个是大小
new_texts=[plt.text(dd[i,0],dd[i,1],texts[i]) for i in range(len(texts))]
#print(new_texts)
adjust_text(new_texts,arrowprops=dict(arrowstyle='->',color='red',lw=0.5))
plt.xlabel('闭卷科因子得分')
plt.ylabel('开卷科因子得分')
plt.savefig('学生因子图.png',dpi=500)
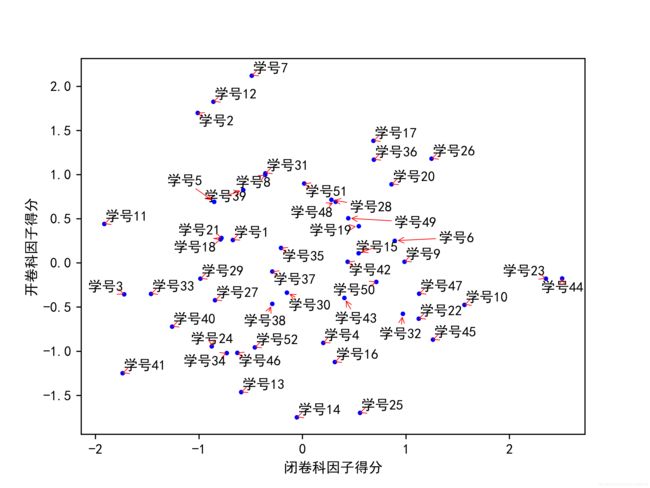
#举个例子说明好处，A7的开卷科因子得分高，说明这个学生开卷很厉害，会抄会找答案，但是可以发现闭卷科因子低
#说明他记的东西少，公式到考场上的时候记不住，考的分低
plt.show()

3.效果

使用adjustText的前的原图：

修正后：

（图像放大前）

（图像放大后）

效果明显好了很多

你们的每个赞都能让我开心好几天✿✿ヽ(°▽°)ノ✿