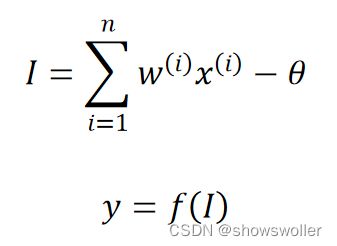【机器学习】算法术语、决策函数、概率模型、神经网络的详细讲解(图文解释)
一、机器学习算法术语
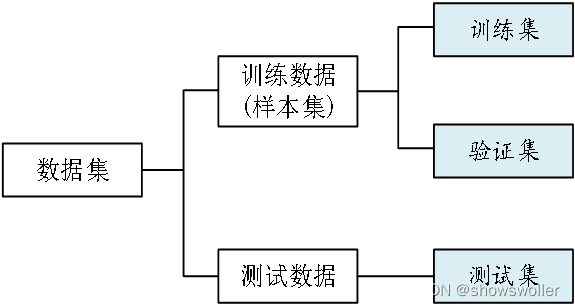
1)数据集(Data Set),训练集(Training Set),验证集(Validation Set)和测试集(Test Set)
数据集分为训练数据和测试数据。测试数据集合即为测试集,是需要应用模型进行预测的那部分数据,是机器学习所有工作的最终服务对象。为了防止训练出来的模型只对训练数据有效,一般将训练数据又分为训练集和验证集,训练集用来训练模型,而验证集一般只用来验证模型的有效性,不参与模型训练。
2)实例(instance),属性(Attribute),特征(Feature),特征值(Feature Value)和特征向量(Feature vector)
实例是一个完整的训练或测试数据,如一张图片、一段文本句子、一条音频等。实例有一般多个属性,因此用多维的向量来表示它,并用粗体的小写字母来标记,如x_i,下标i表示实例的序号。
传统机器学习算法一般不直接对实例的属性进行处理,而是对从属性中提炼出来的特征进行处理。实例通常是由多个特征值组成的特征向量来表示。用特征向量来表示实例时,也用x_i表示。用带括号的上标来区分实例的不同特征,如x_i^(j)表示第i个实例的第j维特征。有m个特征的第i个实例可表示为x_i={x_i^(1),x_i^(2),…,x_i^(m)}。
3)标签(Label)和样本(Sample)
在监督学习中,训练数据不仅包括实例,还包括事先标记好的标签。在分类、聚类和标注模型中,标签是离散编号值,在回归模型中,标签是连续值。对训练数据来说,标签是指导训练的结论,对测试集来说,标签是要预测的目标。
在分类、聚类和回归任务中,标签值一般是一维的标量,一般用y_i表示。在标注任务中,标签值是一个序列,可看成是向量,一般用粗体y_i表示。测试集中的数据只包括实例,标签是需要预测的,在分类、聚类和回归任务中用y ̂_i来表示待预测的标签值,在标注任务中用粗体y ̂_i来表示待预测的标签序列。
样本是一份可用来训练的完整数据。在监督学习中,样本由实例及其标签组成,用s_i=(x_i,y_i)或s_i=(x_i,y_i)表示第i个样本,而实例x_i也称为未标记的样本。在无监督学习中,样本没有标签,可直接用实例表示,即:s_i=x_i。
二、机器学习模型实现算法分类
设样本集S={s_1,s_2,…,s_m}包含m个样本。
对分类和回归任务来说,每个样本s_i=(x_i,y_i)包括一个实例x_i和一个标签y_i,实例由n维特征向量表示,即x_i=(x_i^(1),x_i^(2),…,x_i^(n))。
对聚类任务来说,样本即实例,不包括标签,s_i=x_i=(x_i^(1),x_i^(2),…,x_i^(n))。
对标注任务来说,样本s_i=(x_i,y_i)包括一个观测序列x_i=(x_i^(1),x_i^(2),…,x_i^(n))和一个标签序列y_i=(y_i^(1),y_i^(2),…,y_i^(n))。
1:决策函数模型
决策函数模型是将实例x=(x^(1),x^(2),…,x^(n))与标签y之间的关系看作一种映射,用函数Y=f(X)来表示,X是定义域,它是所有实例特征向量的集合,Y是值域R。
在分类、聚类和回归任务中,模型从样本集中学习到该映射,并依据该映射对测试样本x给出预测值y,用y=f(x)表示。在分类任务中,标签是预先确定的有限个离散值,因此该映射是从实例特征向量集合到有限个离散的映射。在回归任务中,标签是无限多的连续值,因此该映射是从实例特征向量集合到连续值的映射。在聚类任务中,训练之前标签是不确定的(有的算法事先要指定标签的数量),需要算法在训练过程中分析训练样本的分布情况并建立簇结构,从而建立映射关系,依据映射关系给簇内样本分配标签。
常用的决策函数分类模型有决策树、随机森林、逻辑回归、Softmax回归、支持向量机等模型。
常用的决策函数聚类模型有k均值、DBSCAN、AGNES等模型。
常用的决策函数回归模型有决策树、线性回归、多项式回归、局部回归、支持向量机等模型。
2:概率模型
在概率模型中,将实例x=(x^(1),x^(2),…,x^(n))与标签y看作是两个随机变量的取值,随机变量记为X和Y。
机器学习算法能够有效的前提是假设同类数据(包括训练数据和测试数据等)具有相同的统计规律性。
对监督学习来说,假设输入的随机变量X和输出的随机变量Y遵循联合概率分布P(X,Y)。P(X,Y)表示分布函数,或分布概率函数。模型的训练集和测试集被看作是依联合概率分布P(X,Y)独立同分布产生的。
对无监督学习来说,假设输入的随机变量X服从概率分布P(X),模型的训练集和测试集是依P(X)独立同分布产生。
聚类任务的输入是无标签的样本,算法要自行分析样本数据的分布结构形成由条件概率表述的模型P ̂(Y|X),并对测试样本x给出预测簇标签y ̂。有些聚类算法的标签值个数是超参数,要由用户事先指定。有些聚类算法则可以自行确定标签值个数。常用的概率聚类模型有高斯混合聚类模型。
在分类任务中,用条件概率分布函数P ̂(Y|X)来描述从输入到输出的概率映射关系,在训练时,算法要从训练数据中学习到该分布函数。在预测时,对测试样本x,模型计算所有候选标签y的条件概率P ̂(y|x),取最大值对应的y为测试样本x的预测标签值y ̂。常用的概率分类模型有朴素贝叶斯模型、逻辑回归模型。
在标注任务中,输入的x=(x^(1),x^(2),…,x^(n))表示一个可观测的序列,该序列的元素存在一定的关联关系。像天气温度、股票价格、语音数据等,可以看作向后单向关联关系的序列。而像文字句子,句子中的字一般与上文、下文双向语境都有关。
标注任务的输出是与x对应的标签序列y=(y^(1),y^(2),…,y^(n)),标签取值于标签值空间。标签值空间一般远小于观测值空间。也就是说,标注模型输出的也是一个序列,它与输入序列等长。
在训练时,算法要学习到从序列x到序列y的条件概率P ̂(y^(1),y^(2),…,y^(n)|x^(1),x^(2),…,x^(n))。在预测时,按照该条件概率模型以概率最大的方式对新的输入序列找到相应的输出标签序列。具体来讲,就是对一个输入序列x=(x^(1),x^(2),…,x^(n))找到使条件概率P ̂(y^(1),y^(2),…,y^(n)|x^(1),x^(2),…,x^(n))最大的标记序列y ̂=(y ̂^(1),y ̂^(2),…,y ̂^(n))。
常用的概率标注模型有隐马尔可夫模型、条件随机场模型等。
概率模型又可以分为生成模型(generative model)和判别模型(discriminative model)。
生成模型学习到的是联合概率分布P(X,Y),然后由联合概率分布求出条件概率分布作为预测模型: P(Y|X)=P(X,Y)/P(X)
判别模型直接学习到条件概率分布P(Y|X)作为预测模型。
生成模型是所有特征以及标签的全概率模型,它学习到了全面的信息,可以计算出任意给定条件下的概率值,因此可以用到多方面概率预测问题上。而判别模型针对性强,直接面对问题,模型的适应性有限。
3.神经网络模型
人工神经网络(Artificial Neural Network,ANN)简称神经网络(NN),是一种模仿脑结构及其功能的信息处理系统。神经网络在机器学习的分类、聚类、回归和标注任务中都有重要作用。
人工神经元(简称神经元)是神经网络的基本组成单元,它是对生物神经元的模拟、抽象和简化。现代神经生物学的研究表明,生物神经元是由细胞体、树突和轴突组成的。通常一个神经元包含一个细胞体和一条轴突,但有一个至多个树突。
受生物神经元对信息处理过程的启迪,人们提出了很多人工神经元模型,其中影响最大的是1943年心理学家McCulloch和数学家W.Pitts提出的M-P模型。
x^(i)表示来自其它神经元的输入信息,i=1,2,…,n。w^(i)表示输入信息对应的连接系数值。∑表示对输入信息进行加权求和。θ是一个阈值,模拟生物神经元的兴奋“限度”。输入信息经过加权求和后,与阈值进行比对,再通过一个映射,得到输出y。
f(∙)称为激励函数或转移函数,它一般采用非线性函数。
就M-P模型而言,神经元只有兴奋和抑制两种状态,因此,它的激励函数f(∙)定义为单位阶跃函数,输出y只有0和1两种信号。
单位阶跃函数u(∙)不连续,在优化计算时难以处理,常用近似的阈值函数来代替它,例如虚线所示的Sigmoid函数。
单个神经元的作用有限,只能处理线性问题。但如果将神经元连接成神经网络,并采用非线性的激励函数,则具有强大的处理非线性问题的能力。
理论上,可以通过将神经元的输出连接到另外神经元的输入而形成任意结构的神经网络。但目前应用较多的是层状结构。 层状结构由输入层、隐层和输出层构成,其中可以有多个隐层
从信息处理方向来看,神经网络分为前馈型和反馈型两类。前馈型网络的信息处理方向是从输入层到输出层逐层前向传递。输入层只接收信息,隐层和输出层具有处理信息的能力。相邻层之间的节点是全连接关系,同层节点、跨层节点之间没有连接关系。有些特别设计的前馈神经网络会在个别同层节点之间或者个别跨层节点之间引入连接关系,如深度学习中的残差网络。
反馈型网络中存在信息处理反向传递,即存在从前面层到后面层的反向连接。反向传递会使得信息处理过程变得非常复杂,难以控制。
经过设计的神经网络可以用来完成机器学习的分类、聚类、回归和标注任务。
神经网络的网络结构可以看作是有向图,用S表示。神经网络中,每条连接都有一个连接系数,每个隐层节点和输出层节点都有一个阈值,这些参数(包括连接系数和阈值)用W表示。可以用N(S,W)表示神经网络。
一般来讲,网络结构S是预先设计好的,不存在学习问题。神经网络的参数W是通过训练从训练样本集中学习到的。如果通过学习不能达到预想要求,则可能需要重新设计网络结构S。目前在神经网络方面的研究大多是针对某一具体问题提出一个新的有针对性的网络结构S,还没有一个通用的能解决不同问题的网络结构。
传统神经网络模型中,常用于处理分类和回归问题的有BP神经网络,用于处理聚类问题的有SOM神经网络。
在以神经网络为基础的深度学习为特征提取问题提供了有效的解决方法之后,机器学习才得以异军突起,得到广泛应用。深度学习带来的革命性变化是弥合了从底层具体数据到高层抽象概念之间的鸿沟,使得学习过程可以自动从大量训练数据中学习特征,不再需要过多人工干预,实现了所谓的端到端(end to end)学习。
深度学习的具体算法一般是与某类具体应用紧密相关的,如图像识别问题与卷积神经网络、序列标注问题与循环神经网络等,还没有一个通用的模型或结构。
创作不易 觉得有帮助请点赞关注收藏~~~