后缀自动机SAM详解
用一个DFA来识别一个串(比如aabab)的所有后缀,要怎么做呢
最简单的办法,把所有后缀看作要保存的单词,画一棵 trie树,像这样:
点很多很麻烦复杂度也很高
我们给这个DFA按我们的需求合并化简一下,把树升级为DAG,变成下面这样
这个就是我们想要的后缀自动机了
那它怎么构建,有什么特性呢,下面我们就来说一下
1.不论对化简前的 trie树,还是化简后得到的SAM,都具备这样一个结论:
从源点出发到达任意终止结点经过的路径所形成的串一定是原串的一个后缀串
从源点出发到达任意结点经过的路径所形成的的串一定是原串的一个子串,且对不同路径,子串必互不相同
这个DAG可以确定出原串的所有不同子串
2.SAM中,结点所代表的状态本质是一个endpos集,这个endpos集还对应着一个子串集,这个子串集是具有相同endpos的一个等价类
endpos代表子串在原串终止位置的集合,比如aabab中,子串集{a}的endpos集为{1,2,4}
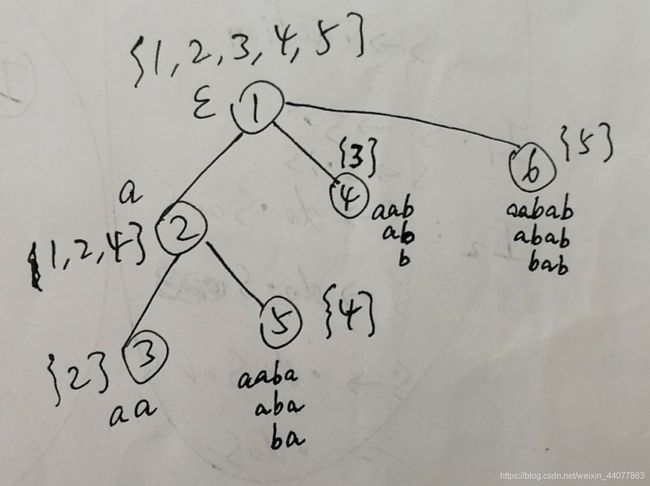
继续以上图为例,aabab
结点1子串集为{ε},endpos集为{1,2,3,4,5}
结点2子串集为{a},endpos集为{1,2,4}
结点3子串集为{aa},endpos集为{2}
结点4子串集为{aab、ab、b},endpos集为{3}
结点5子串集为{aaba、aba、ba},endpos集为{4}
结点6子串集为{aabab、abab、bab},endpos集为{5}
3.结点这个等价类的endpos集和子串集的性质:
①对于一个原子串,在左侧增加字符增长后,endpos要么变少要么不变
比如 ba 和 a,ba 能匹配上的,a也能一定匹配上,ba能匹配的位置只会比 a 少或相等,不会更多
但比如 ba 和 b,这个就没法比较了,ba 和 b 不是后缀包含关系,ba 不是 通过 b 在左侧增加若干字符得到的
②有后缀包含关系的串(s2是s1的真子后缀),其endpos集也必然有包含关系
比如 ba 和 a,ba 能终止的位置,一定是在 a 的 endpos 里选的
我们可以把这个包含关系,按包含传递顺序用父子关系连接,这样不断向父亲遍历,就能找到一个子串的所有子后缀串
比如我们要找子串aaba的所有子后缀串,
首先拿到它所在的结点5 endpos{4},这个等价类中,有串集 aaba、aba、ba
然后找这个等价类的父类2 endpos{1,2,4},找到串集 a
然后找到等价类2的父类1 endpos{1,2,3,4,5},找到串集 ε
至此,所有 aaba 这个子串的后缀子串都被找到
需要注意的是,父类串集中最长的串,是当前类中不满足当前类的endpos的一个最长公共真子后缀,结论③将就这一点进行具体阐释
③每个等价类串集中的串,具有长度连续的特点,且记一个串集中最长的串长为len,最短为minlen,有 len( i ) = minlen( fa( i ) ) + 1
以结点5和结点2为例,结点5表示的最长串尾 aaba,取其最大真后缀串,aba,那么其endpos集含有的元素数可能变多,也可能不变
如果变多,那ba的话也一定比 aaba 多,所以说,随着减少左侧字符不断递减长度,直到endpos元素变多才会不属于aaba所在的等价类
也就是说,这个等价类里的字符串长度是减少左侧字符依次递减的,直到endpos变了,才开一个新类
比如这里结点5就是,串集 aaba、aba、ba不断减少左侧字符递减,直到到 a,endpos变了,a开了一个新类作为5的父类
然后很显然,结点5的直接父类是 aaba 的不满足 endpos(aaba) 的最长真子后缀所在的类
当然 aaba 所有不满足 endpos(aaba) 的真子后缀所在的类都是 aaba 所在类的祖先类,但是未必是直接父类,要明确,怎样才是直接父类
④由一个endpos集得到几个子endpos集的过程实际上是一个不完全划分
盖覆:比如 {1,2,4} 分为 {1,2} 和 {1,4}
划分:比如 {1,2,4} 分为 {1,2} 和 {4} ,划分是一种特殊的盖覆
这里所说的不完全划分是笔者的说法,指的是
不完全划分:比如 {1,2,4} 分为 {2} 和 {4} 丢掉了1这样是可以的,不需要实现盖覆,但是注意一定不存在覆盖
显然,endpos集不完全划分的过程构建的父子关系是一棵多叉树,笔者称其为 endpos 树
实际上关于一个endpos集是否被划分还是不完全划分,这个是可以快速确定的,而且是很重要的,笔者会在最后讲述这个结论
继续以 aabab 为例我们画一下它的 endpos 树,感受一下
⑤SAM的建立就是建立一个DFA和一个endpos树,其建立过程是在线的(按字符串遍历序不断添入字符),其本质是状态转移
比如建立 aababa ,当加入aabab后,当前的结果就是aabab的SAM,只要添入a,就会变成aababa的SAM
下面就来讲SAM的建立过程:
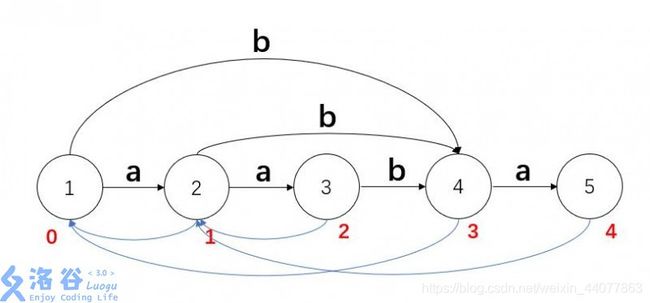
先来看个例子,我们手动推一推
蓝箭头是endpos树,指向父类的箭头
红字记录的是当前结点中串集中最长串的长度len
上图中的信息画到了下面表格中来辅助我们推导
| 状态 | 父类 | len | 串集 |
| 1 | 0 | 0 | ε |
| 2 | 1 | 1 | a |
| 3 | 2 | 2 | aa |
| 4 | 1 | 3 | aab、ab、b |
| 5 | 2 | 4 | aaba、aba、ba |
先来看这样一种情况
case1
比方说现在我们只有前3个结点吧,要把4加进去,要怎么做呢
现在呢,已经构建的串,即原串为aa,很显然任意阶段的最长串,就是原串,我们每次都要记录一下含有最长串这个结点,因为需要用,这里就用pre=3来记录一下
我们现在来了个字符b,新串aab,想知道aab有哪些后缀串,非常简单容易想到的一个做法就是原串 aa 的所有后缀串,后面增添一个 b,就是 aab 的后缀串了
那怎么找 aab 的所有后缀串呢,实际上前置结论已经讲过这个了,利用的就是endpos树
aa所在类3的后缀串有aa,然后继续找它的endpos不同的真子后缀,即不断找父类,到父类2,找到a,然后到父类1,找到ε,然后到达父类0,意味着要收手了,然后这些就是aa的所有后缀串
然后这些串后面加上 b ,就是 aab ab b 了,那我们就把结点0、1、2引出边b指向结点4
把4的父类置为1,为什么呢,很显然只有1是4的最长不符endpos(4)的真子后缀
当然这样说父类怎么置的那就成了我们用眼睛看出来的,那我们继续看下一种情况,弄清这个父类到底怎么确定的
case2
已经建好了原串aab的SAM,现在加入字符a
结点4和结点1,有着 aab 所有后缀串 aab ab b ε
那好,我们给结点1和4分别引一条边a指向结点5,对吗?显然错的啊,1通过a到5表示的是后缀串a对吧,a已经有了不是吗?你看1到2不就是吗?
想起来我们最一开始讲的 trie 按需化简为 DAG 了吗,1到5是多余的,那怎么回事,很简单呀,就是你看到的那样,前面已经出现过了这样的子后缀
因为 1 已经有一个 a 边引到 2 了,可能看到这里你有些懵逼,不是说好的原串所有后缀都加新的字符吗
确实是这样,但这不代表所有相关结点都这样做,那怎么判断呢
抛开这道题,我们随便举个例子去说说吧
比如一个结点 p 串是 ababa,父结点 pp 串是 baba,父的父 ppp 串是 aba、ba,父的父的父 pppp 串是 a,父的父的父的父 ppppp 串是 ε
其中 ppp 结点通过b指向一个结点 x,p和pp结点没有引出的 b 边
然后现在新加入一个 b,首先 p 要引出一个 b 边到新节点y,得到 ababab,然后找p的父亲pp,引一个b边到y得到babab,然后找到 ppp
发现 ppp 已经有引一个b边到 x 了,且abab是x中的一个最长串集,abab、bab已经有了,那就不用再让 ppp 引b到y了,问题来了,还需要继续判断 pppp 和 ppppp 吗
ab 和 b是否已经都有了呢
思考这样一个问题,结点 x 的串集是什么,根据我们前面假设的条件,一定有 abab 和 bab 吧,ab 和 b 有没有呢,不知道,但是x没有的话,结点x的祖先类也一定有
那就好办了,那就是说 abab bab ab b 都有了
那于是只有 p 和 pp 要引 b 到 y
那 y 的串集就是 ababab 和 babab 了,那 y 的父类是谁,显然是结点 x 了,这个就没什么说明的意义,很显然了
case1的时候我们就说,父类怎么确定,其实现在还没太说清楚,但是情况大致搞明白了,对于case1中找父类的循环我们也做了调整,终止位置明确了
根据上面这些例子,我们可以得出这样的暂时结论
对于已经构建的SAM,含有最长串的结点记作p,新加入一个字符c,我们记新构建的结点为np
从 p 开始,如果 p 没有引出的 c 边,那么就从 p 引出 c 边到np,记 p.ch[c] = np,然后令 p = fa( p ),继续循环判断
直到 q = p.ch[c] 存在,那就不用引了,之后的父类也不用判了,按前面说的令 fa( np ) = q 就ok了,结束
当然也有可能所有结点都没有 ch[c] ,这时候一直跑父类就跑到 0 了,当然这时候其实 q 就是 1,fa( np ) = 1(这里现在是同一用q,但之后写法还要做调整,其实还有其他情况)
那好了,fa ( np ) = q 真的对吗
用上面我们随便举的那个例子去看,挺对的,但注意我们有个很重要的假设前提,结点 x 的最长串是 abab,不妨设想,没有这条假设,或许ppp通过其他某一路径到x,
x中的串集还可能有 abacb 之类更长的串,而我们知道,我们是要原串后加一个b,ababa及其所有真子后缀是要加 b 的,且都存在于结点 p 及其祖先类结点
而显然 结点ppp通过一个字符 c 到达的其他结点一定不是这些类,也就是 abac 一定不是原串 ababa 的后缀,再加上b,abacb 就一定不是我们新串 ababab 的后缀
那就很明显了,结点 x 的最长串一定得是 通过结点 ppp 得到的,那我们的变量 len 记录结点中最长串的长度,这个变量就派上用场了
前面的结论就改作 len( q ) == len ( p ) + 1 时才允许 fa( np ) = q,然后结束
那 len( q ) != len ( p + 1 ) 的话要怎么办呢,我们来看下面这样一个例子
为方便看,还是先放两个表格,一个是只建到5的,即上一个我们看过的那个表,一个是现在这个图对应的表
| 状态 | 父类 | len | 串集 |
| 1 | 0 | 0 | ε |
| 2 | 1 | 1 | a |
| 3 | 2 | 2 | aa |
| 4 | 0 | 3 | aab、ab、b |
| 5 | 2 | 4 | aaba、aba、b |
| 状态 | 父类 | len | 串集 |
| 1 | 0 | 0 | ε |
| 2 | 1 | 1 | a |
| 3 | 2 | 2 | aa |
| 4 | 7 | 3 | aab |
| 5 | 2 | 4 | aaba、aba、ba |
| 6 | 7 | 5 | aabab、abab、bab |
| 7 | 1 | 2 | ab、b |
case3
p=pre=5,nq=6,p.ch['b']为空,令p.ch['b']=nq
然后找 p = fa( p ) = 2,发现 q = p.ch['b'] = 4,跳出找父类的循环
然后 len(2) + 1 != len( 4 ),不能让 fa( np ) = q = 4,于是要怎么办
2 的串集是 a,以 2 为汇点,表示的后缀串是 a、ε,我们希望得到 ab、b
但是 2 通过 b 通向的 4表示的是 aab、ab、b,多了个 aab,原因是 2 还有一条路径,通过 a 通过 b 然后到达 4
那怎么办,那就把结点 4 分裂,分出一个表示 ab 和 b 的结点,自己保留对 aab 的表示
分裂出一个结点记作 nq=7
我们的目标是什么,串 a 及其所有子串要通过 b 到达 nq 对吧,
从结点 2 开始,不断找父类 p = fa( p ) ,只要 p.ch['b'] 存在,直到 p.ch['b'] 不存在为止就停下,那就应当指向结点 nq=7
模板里循环条件一般写的是 p.ch['b'] == q,但其实你想一想,这时候 p.ch['b'] 如果存在则一定指向的是 q
构建过程怎样的,为什么是这样的,我想看到这里客官一定已经能够自行理解了,就不在赘述了
分裂出的这个结点 nq=7,要注意,它是原来结点 q=4 功能的一部分,后面可以接 'a' 到 5 的,换言之我们要把 q 的 ch 数组复制给 nq.ch
然后我们就可以令 fa ( np ) = nq 也就是 fa( 6 ) = fa ( 7 )
然后需要注意的是 还要令 fa(q) = nq 也就是 fa( 4 ) = fa( 7 ),因为拆分出的这部分是 4 中短的部分,你可以看作 0 到 4 中间加了个中继节点 7,并且是由于7有额外功能才加的
然后这时候要注意 pre和num的更新,pre=6 而不是 7,总结点数 num=7 而不是 6
于是这个SAM构建算法描述为下面这样:
每个结点需要记录的变量:fa、len、ch[k] k是数组长度,是字母表大小(比如串里只有小写字母那就26,字符c对应下标 c-'a')
pre记录原串中最长后缀串(就是原串)所在的结点编号,初始为pre=1,num记录总结点数,初始为num=1
按字符串遍历序,不断add(c),这里 c 已经对应于ch的下标大小了,比如小写字母减去'a'后的int
add(c)算法描述
①待添加字符 c,令 p=pre,np=pre=++num,对结点 a[p],如果 a[p].ch[c] 不存在,则令 a[p].ch[c]=np,然后令 p = a[p].fa,继续循环重复上述判断,直到 a[p].ch[c] 存在跳出循环
②如果 跳出时 p=0,则令 a[np].fa=1,结束
否则 令 q = a[p].ch[c]
③如果 len(q) == len(p)+1,则令 a[np].fa = q,结束
④否则 分裂结点 q,令 nq=++num,令 a[nq]=a[q](本质是为了赋ch),然后对结点 a[p],如果 a[p].ch[c]==q,则令 a[p].ch[c]==nq,然后令 p=a[p].fa,继续循环重复上述判断,直到 a[p].ch[c]==q 不成立跳出循环,最后令 a[np].fa=nq,结束
还需要一提的是时间 空间问题
首先时间复杂度 O(nlogk),n是字符串长度,k是字母表大小,一般来讲logk基本就是常数,可以复杂度看作 O(n),但建议记前者
空间上,结点数量是需要考虑的
回忆前面讲的endpos树,SAM这个DFA本质还是一棵endpos树,而这个树是对endpos集不断做不完全划分得到的
而区间划分结点最多的情况就是线段树,最多2n-1个结点,即<2n
我们这里开 maxn<<1 就够了,但要注意别糊涂了,线段树因为其他原因开的是 maxn<<2
下面是模板代码
#pragma GCC optimize("Ofast")
#include
#define maxn 1000005
using namespace std;
struct node{
int ch[26];
int len,fa;
}a[maxn];
int pre=1,num=1;
void add(int c){
int p=pre,np=pre=++num;
a[np].len=a[p].len+1;
for(;p&&!a[p].ch[c];p=a[p].fa) a[p].ch[c]=np;
if(!p) a[np].fa=1;
else{
int q=a[p].ch[c];
if(a[q].len==a[p].len+1) a[np].fa=q;
else{
int nq=++num;
a[nq]=a[q];
a[nq].len=a[p].len+1;
a[q].fa=a[np].fa=nq;
for(;p&&a[p].ch[c]==q;p=a[p].fa) a[p].ch[c]=nq;
}
}
}
char s[maxn];
int main(){
scanf("%s",s);
int len=strlen(s);
for(int i=0;i 到这里SAM的解析就已经结束了
下面讲一讲最常见的应用
1、判断子串
直接在SAM上从源点出发跑,在跑到null之前,输入串就被识别完了,那就是原串的一个子串了
2、不同子串个数
本质是统计源点出发到达任意点一共有多少条路径,DAG上DP,dp(i)为从结点 i 出发的路径数(也就是从 i 出发的子串数)
dp( fa( i ) ) += dp( i ) + 1,然后 dp( 1 ) 就是我们要的答案
还有一种方法也很棒,SAM上所有串都是不重复的嘛,每个结点所表示的串集加在一起就是答案了嘛
那串集大小是多少呢,这个也很重要,len( i ) - len( fa( i ) )就是结点 i 的串集大小,因为长度连续嘛
比如结点 i 表示的是 abcde bcde,那结点 fa(i) 最长的一定是 cde
3、所有子串中字典序第 i 大的串(重要)
如果是所有不同子串中字典序第 i 大的,那就相当简单了,用2中统计好的个数DFS一点点判就好
但现在可以重复计算了,那就得变一变
其实也很简单,就是个带权DAG,路径带上了遍数
不妨设想,a到b走了4遍,a过b到c走了2遍,a过b到d走了3遍,那也就是说b到c走了2遍,b到d走了3遍,从b出发走了5遍
其记录方式还是原来的 dp 累加,只不过加的不是 1 了
不过要注意的是,答案是 4+5=9,而不是4*5=20
因为 a过b到c 走了2遍,你看作b到c走了2遍,那就是a过b到c看作a到b走了1遍,然后b到c走了两遍
实际上也确实是这样,那个4和 2、3是没关系啊,终点都不一样,不是经过遍数
那 a 到 b 经过的遍数肯定是 9 啊,其实你这么一想,这个答案倒也是 a 到 b经过的遍数
为什么我们前提是这个,a过b到c走了2遍,a过b到d走了3遍,因为SAM的endpos就是这样,a到 i 这个路径走过多少遍,就是endpos的元素数
那问题就只剩 cnt(endpos(i)) 怎么统计了
这时候就有一个很重要的结论了
重要结论:
当一个结点是分裂来的结点时,其endpos集被划分为其各个子集
当一个结点不是分裂来的结点时,若其有子集,则其endpos集必然被不完全划分为其各个子集,且丢掉的元素必然有且只有一个
所以在这里,每个不是分裂来的结点,且不是初始结点的结点,其cnt值可直接初始为1,cnt(fa(i))+=cnt(i)
为什么会有这样一个结论呢
不妨设想建立过程,某个结点p,什么时候才有的儿子,才被作为父亲指向,是作为儿子的真子后缀再次成为后缀串的一员的时候
那一个儿子都没有的时候呢,显然结点p的串集中的子串只出现过一次,endpos集的大小必然为1
而刚增加一个儿子,儿子的endpos集大小也必然为1,而父亲也会拥有儿子这个endpos位置,父亲endpos集增加的都是来源于儿子的,而父亲自己的依然是自己的
这使我们掌握了endpos树的一个特性
实际上通过这个我们也了解到了endpos树的叶子结点的endpos集大小就是1
然后说分裂来的结点,与分裂前的结点相比,是把原来结点串集拎出一部分短串来,endpos集都是一样的,没有自我,没有独属于自我的endpos位置,这是很明显的,不再赘述了
4.多个串的最长公共子串(重要)
先说两个串的,O(n)解决,非常的简单,给你串s和t,先用s建一个sam,然后 t 从头开始匹配
打个比方,比如 t 是 abcbdac,匹配了结点x的 abcb,匹配的len=4,然后找不到 d 了,于是在 endpos 树上跳向父亲,缩减长度到真子后缀,就类似于尺取一样
那跳回后怎么看len呢,一定是sam记录的 a[p].len,因为很显然啊,就算你匹配结点x匹配的是串集中最短的,那也比结点p中的要长,毕竟p中的都是x中的真子后缀
比如跳回去的结点是 cb、b,那最长的 cb 一定是能匹配的,然后接着做看有没有d就行,重复操作就好,特别的是可能会跳回到结点0,这时候就应该跳到1来重新进行匹配,并且len也要清0
多个串怎么办呢
思路不难,类似的思想O(n^2)解决,对s1建立SAM,然后对s2...st,每个都在SAM上跑一轮
用一个 mx 数组记录当前轮中(也就是每轮清零),si在SAM上跑完,每个结点能匹配的最大子串长度
这里有个细节要注意,跑的时候 结点 p 可能匹配了长度2,单是最长a[p].len=4,而子类q可能匹配成了
那你最后回去 mx(p) 记录的应该是 4 ,而不是 2,这里最后要O(n)判一次
但要注意的是,结点编号序其实有点乱,我们这样跑肯定要先子后父式的更新
其实怎么说,上面那个情况看起来可能就算父子顺序不太对也没大问题,但是啊,举个例子
匹配了 abb,比如有个父亲 bb,bb的父亲 b,那跑SAM的时候 bb 肯定是 0 啊,但是最后 bb 和 b 都要变成 len,你顺序错了,b 不知道 bb 不是0,b 的更新就不对了
然后讲这个顺序怎么调依据 len 的特点,len更小则一定不是len大的儿子,只能是父亲,或者是不相干的,len相等,一定不相干,那就好办了,按len排点就行了
在我的理念中,这里开个新的结构体数组 O(nlogn) 快排一下就好,没必要整些麻烦事挑战自己
网上代码基本都是巧妙的O(n)调整了顺序存到一个新的数组里,看着类似基数排序
讲真,没必要挑战自己,总的复杂度O(n^2)
不过有一份代码贼蠢,每轮处理他都排序一次,受不了,太蠢了,那可不嘛,你每次都排那可不O(n^2)嘛,看着排序挺聪明的,但是代码很蠢
然后mx说完了
然后用一个mn[ i ] 数组更新记录每个结点 i 所有轮中匹配的 mx[ i ] 中的最短长度,很好理解,就是得每个串都能匹配的上嘛
最后跑一遍 mn 找出 max mn 就行了,还是很好理解的,不是很难,但是很重要,要会,尤其前面那里的求 mx 时的特判尤其重要一定要特别注意
就说这么多了,本篇博文到这里就结束了,希望看官能够从这篇博文里有所收获