【图嵌入】DeepWalk原理与代码实战

DeepWalk

基础理论

了解过 NLP 的同学对 word2vec 应该不陌生，word2vec 通过句子中词与词之间的共现关系来学习词的向量表示，如果你忘记了，可以看看我之前的博客：

1. 【word2vec】篇一：理解词向量、CBOW与Skip-Gram等知识
2. 【word2vec】篇二：基于Hierarchical Softmax的 CBOW 模型和 Skip-gram 模型
3. 【word2vec】篇三：基于Negative Sampling 的 CBOW 模型和 Skip-gram 模型

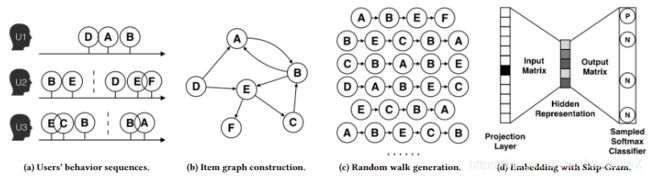
DeepWalk 出自论文：DeepWalk: Online Learning of Social Representations，它的思想与 word2vec 类似，从一个初始节点沿着图中的边随机游走一定的步数，将经过的节点序列视为句子。那么，从不同的起点开始的不同游走路线就构成了不同的句子。当获取到足够数量的句子（节点访问序列）后，可以使用 skip-gram 模型对每个节点学习其向量表示。这个过程如下图所示：

以下是对 DeepWalk 的一些思考与个人理解：

DeepWalk 利用类似深度优先遍历的方式将复杂的图结构转换为序列，进而实现节点的Embedding。这个遍历的过程相当于对图中的节点进行采样，捕获局部上下文信息。上图中B与D都是A与E共有的邻居，那么在经过节点Ｂ、Ｄ的随机游走序列中，节点Ａ或者节点Ｅ出现的频率也比较高，说明节点A和E具有相似的上下文语境，那么A和E的Embedding表示也应该相似。

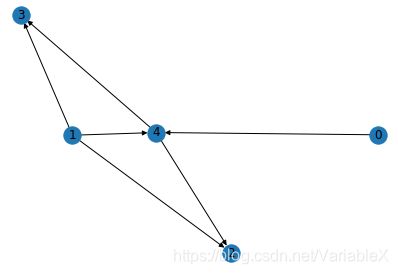
下面再来看个更直观的例子，如下图中的节点1、4是节点2、3共有的邻居：

那么在经过节点1、4的随机游走序列中，节点2或者节点3出现的频率也比较高，例如：

• 0，4，3
• 0，4，2
• 1，2
• 1，3
• 1，4，3
• 1，4，2
• …

那么根据 skip-gram 模型的思想，节点2，3的局部上下文语境比较相似，于是最终学习到的节点2、3的Embedding表示也就比较相似。这也意味着，当两个节点共有的邻居节点越多，那么这两个节点就越相似。

代码实现

结合上面的理论基础，要使用 DeepWalk 得到节点的向量表示，需要分为三个步骤：

1，构造图

主要是使用 networkx 这个库来从文件中读取边的信息来构造图，文件的每一行分别是：

node1 node2 
node1 node3 
......

其中，边的权重 edge_weight 不是必须有的。具体读取数据并构造图的代码如下：

import networkx as nx
# create_using=nx.DiGraph() 表示构造的是有向图
G = nx.read_edgelist('data/wiki/Wiki_edgelist.txt', create_using=nx.DiGraph())

2，随机游走

下面是生成随机游走序列的代码：

import random

# 从 start_node 开始随机游走
def deepwalk_walk(walk_length, start_node):
    walk = [start_node]
    while len(walk) < walk_length:
        cur = walk[-1]
        cur_nbrs = list(G.neighbors(cur))
        if len(cur_nbrs) > 0:
            walk.append(random.choice(cur_nbrs))
        else:
            break
    return walk

# 产生随机游走序列
def _simulate_walks(nodes, num_walks, walk_length):
    walks = []
    for _ in range(num_walks):
        random.shuffle(nodes)
        for v in nodes:
            walks.append(deepwalk_walk(walk_length=walk_length, start_node=v))
    return walks

# 得到所有节点
nodes = list(G.nodes())
# 得到序列
walks = _simulate_walks(nodes, num_walks=80, walk_length=10)

3，嵌入

为了方便起见，这里就使用 gensim 中的 Word2Vec 来实现节点的 Embedding 了：

from gensim.models import Word2Vec
# 默认嵌入到100维
w2v_model = Word2Vec(walks,sg=1,hs=1)
# 打印其中一个节点的嵌入向量
print(w2v_model['1397'])

输出为：

array([-3.57212842e-01, -4.52286422e-01,  1.20047189e-01,  9.33077093e-03,
       -4.87361886e-02,  6.53029561e-01,  3.87212396e-01, -4.35320556e-01,
        4.67856340e-02, -4.55924332e-01, -5.82973696e-02,  1.50977358e-01,
        ......,
       -1.48566559e-01,  4.78760689e-01,  9.73562971e-02, -5.75734824e-02,
       -2.45316476e-01, -2.85568893e-01,  2.79851675e-01,  3.75600569e-02],
      dtype=float32)

优点分析

使用随机游走有两个好处：

• 并行化，随机游走是局部的，对于一个大的网络来说，可以同时在不同的顶点开始进行一定长度的随机游走，多个随机游走同时进行，可以减少采样的时间。
• 适应性，可以适应网络局部的变化。网络的演化通常是局部的点和边的变化，这样的变化只会对部分随机游走路径产生影响，因此在网络的演化过程中不需要每一次都重新计算整个网络的随机游走。

参考文章：

Graph Embedding：从DeepWalk到SDNE - 知乎

【Graph Embedding】DeepWalk：算法原理，实现和应用