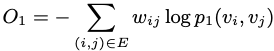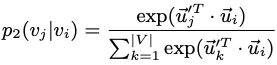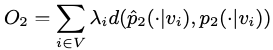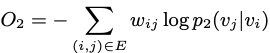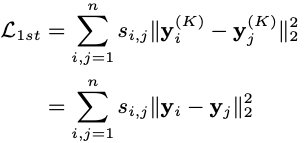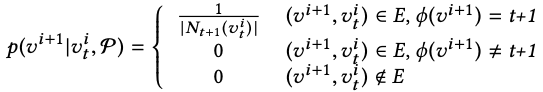Graph Embedding:工业界常用的6种图表示学习方法
导语 | Graph Embedding属于表示学习的一种,目的是通过图的拓扑结构学习得到图中节点的低维稠密表示,从而更方便地应用于下游任务。本文介绍部分工业界常用的Graph Embedding方法,关于Graph Embedding的更全面的介绍可以参考这篇综述文章[1]。
一、DeepWalk
首先介绍2014年提出的deepwalk[2]模型,之前有接触过word2vec方法的同学看这个模型应该会觉得非常简单,算法流程如下所示,首先将所有节点顺序打乱,然后以每个节点为起点,通过随机游走的方式生成一条序列,生成了序列之后,就可以通过word2vec中的skipGram算法来学习节点的embedding表示了。
随机游走的过程非常简单,就是在每个节点处随机选择该节点的邻居节点作为序列的下一个节点,一直走到序列的最大长度后停下来。对于带权重的图或者有向图来说,也可以根据实际情况改变随机游走的策略:比如对于节点i来说,如果他和每个邻居之间的边权重有大有小,可以让节点i走向邻居节点的概率正比于边权重。
由于skipGram算法学习过程是用当前节点的表示来预测邻居节点,因此两个节点如果在图中共有的邻居点越多,则两个节点学到的embedding表示就越相似。
二、Node2Vec
Node2Vec算法[3]在DeepWalk算法上做了一点小改进,主要是改变了随机游走生成序列的过程,使得在学习embedding的过程中会对图节点的同质性(homophily)和结构性(structural equivalence)做权衡,得到序列之后同样使用skipGram算法来学习节点的embedding表示。
同质性和结构性的含义可以从下图进行说明,同质性表示两个相连的节点应该具有相似的embedding表示,如图中节点u和节点S₁直接相连,则他们的embedding应该距离较近。结构性表示两个结构上相似的两个节点应该具有相似的embedding表示,如图中节点u和节点S₆分别处在两个集群的中心位置,则这两个节点的embedding应该比较相似。
为了学习到同质性和结构性,本文探究了两种图的游走的方式:广度优先遍历(BFS)和深度优先遍历(DFS),BFS倾向于在初始节点的周围游走,因此侧重于学习到网络的结构性,DFS倾向于游走到离初始节点较远的节点,因此侧重于学习到网络的同质性。这里我是这么理解的,如上图所示,节点u和节点S₆分别处于两个集群的中心位置,如果使用BFS进行游走,则生成的序列一定都会大量出现中心位置的节点,后续的skipGram算法对于这两个中心位置的节点就有可能学习到相似的embedding表示。相反,如果采用DFS算法,距离较远的两个节点就更有可能出现在生成的同一条序列中,这两个节点会有许多相同的上下文节点,因此后续skipGram算法能够学习到相似的embedding表示。
至于如何控制BFS和DFS的权衡,文中是引入了两个超参数来控制随机游走。
上图表示从节点t出发走到了节点v,接下来从节点v出发跳转到周围节点的概率,Node2Vec随机游走到下个节点的概率可以公式化地表达成:
![]()
其中,![]() 表示边的权重,Z表示归一化系数。
表示边的权重,Z表示归一化系数。![]() 表示节点t就是节点x本身,
表示节点t就是节点x本身,![]() 表示节点t和节点x距离为1(直接相连),
表示节点t和节点x距离为1(直接相连),![]() 表示节点t和节点x距离为2(不直接相连)。
表示节点t和节点x距离为2(不直接相连)。
由公式可以看出,通过调节参数p和q,能够对随机游走的方式作调整:
p被称为返回参数(return parameter),p越小,则节点v走回节点t的概率越大,随机游走更倾向于BFS
q被称为进出参数(in-out parameter),q越小,则节点v更有可能走向远处的节点,随机游走更倾向于DFS
因此,Node2Vec是根据![]() 来挑选下一个节点的,值得一提的是,在具体实现的时候,作者采用AliasSample算法来优化采样过程的时间复杂度,关于这一算法的介绍可以参考这篇博客,讲得十分清楚:
来挑选下一个节点的,值得一提的是,在具体实现的时候,作者采用AliasSample算法来优化采样过程的时间复杂度,关于这一算法的介绍可以参考这篇博客,讲得十分清楚:
https://blog.csdn.net/haolexiao/article/details/65157026
三、LINE
LINE(Large-scale Information Network Embedding)[4]在图上定义了两种相似度:一阶相似度和二阶相似度。通过这两种相似度来约束节点embedding的学习。
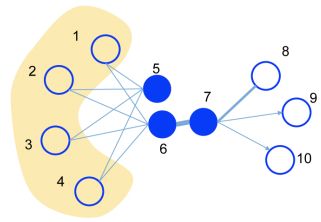
一阶相似度衡量的是图结构中两个相连节点之间的相似度,如果两个节点不存在连边,则一阶相似度为0(如上图中节点5和节点6),如果两个节点相连且边权很大,则这两个节点一阶相似度较高(如上图中节点6和节点7)。一阶相似度刻画了图的局部结构。
二阶相似度衡量的是图网络中两个节点的邻居的相似程度,如果两个节点有很多相同的邻居节点,则这两个节点的二阶相似度较高,即使这两个节点不存在直连边(如图中节点5和节点6)。二阶相似度刻画了图的全局结构。
因此,LINE的优化目标分为一阶相似度和二阶相似度的优化。
1. 一阶相似度优化目标
两个节点的一阶相似度表示为:
![]()
其中W表示所有边权重![]() 之和。
之和。
两个节点embedding的相似度表示为:
其实就是两个节点的embedding内积通过sigmoid函数的结果。
一阶相似度的优化目标表示为实际一阶相似度和节点embedding相似度的KL散度,去掉常数项可以表示为:
文中提到一阶相似度优化目标只用于无向图。
2. 二阶相似度优化目标
二阶相似度优化目标可用于有向图和无向图。文中以有向图为例子介绍了二阶相似度优化目标(无向图可以看成特殊情况的有向图,即一条无向边可以表示成两条权重相同但方向相反的有向边)。
这里LINE对每个节点定义了两个embedding,一个是节点本身的embedding(记![]() ),另一个是节点作为其他节点邻居时的embedding(记为
),另一个是节点作为其他节点邻居时的embedding(记为![]() )。
)。
其中|V|表示节点总数量。
![]()
其中![]() 是边(i,j)的权重,
是边(i,j)的权重,![]() 是节点 i 的出度
是节点 i 的出度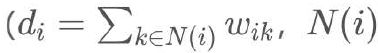 表示从节点i出发的有向边指向的所有节点的集合)。
表示从节点i出发的有向边指向的所有节点的集合)。
二阶相似度的优化目标同样是两个分布的距离:
文中认为不同节点的重要性不同,因此用λi进行加权,为了方便,文中设置![]() 。用KL散度来刻画两个分布的距离并去掉常数项,则上述优化目标可以表示成:
。用KL散度来刻画两个分布的距离并去掉常数项,则上述优化目标可以表示成:
前面提到每个节点会学到两个embedding![]() ,最终是把
,最终是把![]() 用于作为节点的表示。在二阶相似度优化目标的约束下,如果两个节点有许多相同的邻居,且和这些邻居的权重也相似,这两个节点学到的embedding会比较相似。
用于作为节点的表示。在二阶相似度优化目标的约束下,如果两个节点有许多相同的邻居,且和这些邻居的权重也相似,这两个节点学到的embedding会比较相似。
如果要获得同时包含一阶相似度和二阶相似度的embedding,只需要将两者获得的embedding拼接即可。文中也指出可以通过联合优化的方式直接学到包含一阶相似度和二阶相似度的embedding,但文中没有实现。
四、SDNE
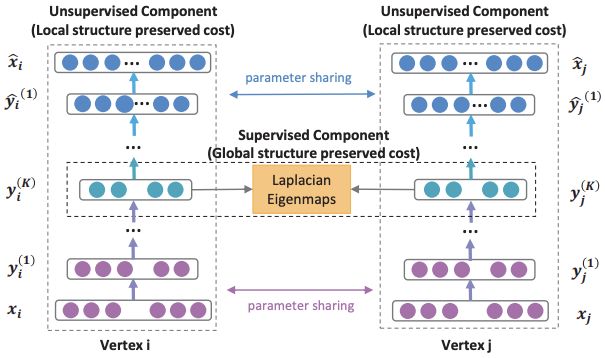
SDNE(Structural deep network embedding)[5]使用深度自编码器架构来学习图节点的embedding表示,通过损失函数约束模型学到的embedding表示能够包含图网络结构的一阶相似性和二阶相似性。其中,一阶相似性表示图网络中直接相连的节点对应该具有相似性,二阶相似性表示两个节点如果有大量共同的邻居节点,则这两个节点的表示应该相似。一阶相似性反映图网络的局部结构,二阶相似性反映图网络的全局结构。
SDNE模型的架构如下所示,模型的输入![]() 是图的邻接矩阵的第i行,表示的是节点i和网络中所有节点的连接情况,通过编码器将输入映射到低维向量空间,得到低维向量表示
是图的邻接矩阵的第i行,表示的是节点i和网络中所有节点的连接情况,通过编码器将输入映射到低维向量空间,得到低维向量表示![]() ,再通过解码器重构回去。因此具有大量相同邻居的节点通过自编码器网络学到的embedding表示会比较相似,这保持了图网络的二阶相似性。另外,对于有直连边的节点对,SDNE会约束两个节点的embedding表示接近,从而保持了图网络的一阶相似性。
,再通过解码器重构回去。因此具有大量相同邻居的节点通过自编码器网络学到的embedding表示会比较相似,这保持了图网络的二阶相似性。另外,对于有直连边的节点对,SDNE会约束两个节点的embedding表示接近,从而保持了图网络的一阶相似性。
SDNE的损失函数如下所示,由三部分组成:一阶相似度损失、二阶相似度损失和L2正则项。
其中,一阶相似度损失表示为:
![]() 表示邻接矩阵S中的一项,
表示邻接矩阵S中的一项,![]() 大于0表示节点i和节点j之间存在连边。一阶相似度损失用于约束存在连边的两个节点学到的embedding表示接近。
大于0表示节点i和节点j之间存在连边。一阶相似度损失用于约束存在连边的两个节点学到的embedding表示接近。
二阶相似度表示为:
可以看到这是一个加权的重构损失,当![]() =0时,
=0时,![]() =1,否则
=1,否则![]() 。之所以要进行加权,是因为图的连边非常稀疏,邻接矩阵S中存在大量零值,自编码器在重构时即使把所有值都输出为0也能取得不错的效果,但这不是我们想要的。SDNE的解决方案是对非零值施加了更高的惩罚系数。
。之所以要进行加权,是因为图的连边非常稀疏,邻接矩阵S中存在大量零值,自编码器在重构时即使把所有值都输出为0也能取得不错的效果,但这不是我们想要的。SDNE的解决方案是对非零值施加了更高的惩罚系数。
五、EGES
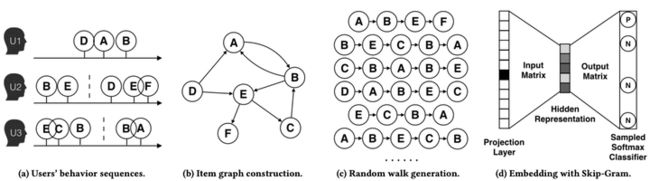
在推荐系统场景中,可以通过user的行为序列构建item的同构图,然后在图中使用随机游走生成序列,再通过skipGram算法获取item的embedding表示,过程如下所示:
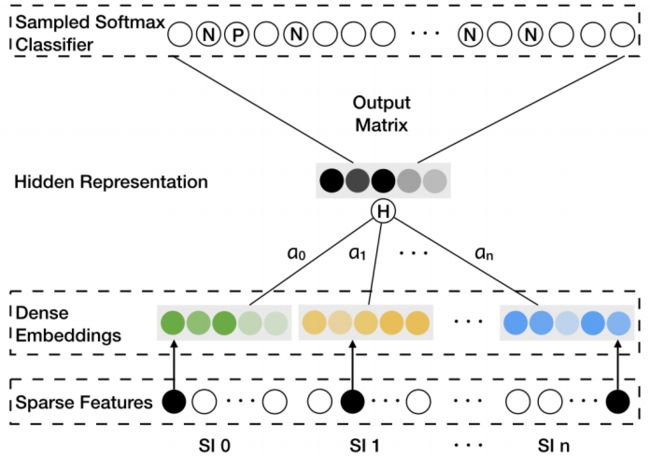
然而,实际推荐场景下不可避免会遇到稀疏(item只在很少的user行为序列中出现)和冷启动(新加入的item)的问题,这会导致对这些item学到的embedding效果很差。推荐场景下一般会通过引入side information(如item的种类、店家、价格等等)的方式来解决这些问题。EGES(Enhanced Graph Embedding with Side Information)算法[6]则是将side information引入到graph embedding的学习过程之中,EGES的模型如下所示:
其中,“SI 0”表示item自身,而“SI 1”到“SI n”则表示n个side information。可以看到,和普通的skipGram不同之处在于,EGES是用各个embedding加权求和获得的hidden representation来预测上下文的item的。另外需要注意的是,实际中EGES是用![]() 而不是
而不是![]() 来作为加权和的权重的。
来作为加权和的权重的。
六、Metapath2Vec
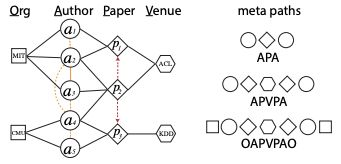
前面介绍的都是基于同构图的graph embedding方法,直接用于异构网络效果不好,因此,Metapath2Vec方法[7]被提出并用于学习异构图节点的embedding表示。
metapath2vec算法仍然采用了随机游走+skipGram的方案,只是在随机游走的阶段做了改进。如下图所示,左边是一个异构图(图上有作者、论文、会议、单位等多种类型的节点),Metapath2Vec算法会先定义metapath,然后根据metapath来进行随机游走,如下图右边就定义了三种metapath,metapath是对称的。
定义了metapath之后,就可以根据metapath进行随机游走了。假设当前节点为![]() (表示节点
(表示节点![]() 是t类型的节点),则产生下一个节点为
是t类型的节点),则产生下一个节点为![]() 的概率为:
的概率为:
公式的三行分别表示:
若两节点存在连边,且下一节点类型和metapath定义的下一节点类型(即类型t+1)相同,则概率为和
 相连的所有t+1类型的节点数的倒数
相连的所有t+1类型的节点数的倒数若两节点存在连边,但下一节点类型和metapath定义的下一节点类型不同,则概率为0
若两节点不存在连边,概率为0
随机游走获得节点序列之后,就可以通过skipGram算法学习节点embedding了:
如上图所示,文中还提出了metapath2Vec++算法,和metapath2Vec算法唯一不同之处在于:在skipGram过程中负样本只使用和正样本同种类型的节点。
参考文献:
[1] Goyal P, Ferrara E. Graph embedding techniques, applications, and performance: A survey[J]. Knowledge-Based Systems, 2018, 151: 78-94.
[2] Perozzi B, Al-Rfou R, Skiena S. Deepwalk: Online learning of social representations[C]//Proceedings of the 20th ACM SIGKDD international conference on Knowledge discovery and data mining. 2014: 701-710.
[3] Grover A, Leskovec J. node2vec: Scalable feature learning for networks[C]//Proceedings of the 22nd ACM SIGKDD international conference on Knowledge discovery and data mining. 2016: 855-864.
[4] Tang J, Qu M, Wang M, et al. Line: Large-scale information network embedding[C]//Proceedings of the 24th international conference on world wide web. 2015: 1067-1077.
[5] Wang D, Cui P, Zhu W. Structural deep network embedding[C]//Proceedings of the 22nd ACM SIGKDD international conference on Knowledge discovery and data mining. 2016: 1225-1234.
[6] Wang J, Huang P, Zhao H, et al. Billion-scale commodity embedding for e-commerce recommendation in alibaba[C]//Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. 2018: 839-848.
[7] Dong Y, Chawla N V, Swami A. metapath2vec: Scalable representation learning for heterogeneous networks[C]//Proceedings of the 23rd ACM SIGKDD international conference on knowledge discovery and data mining. 2017: 135-144.
作者简介
庄万青,腾讯游戏高级研究员,负责游戏玩家行为序列建模,毕业于华南理工大学计算机学院。