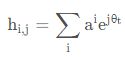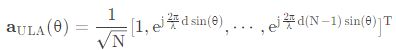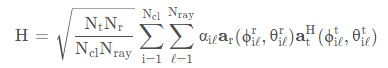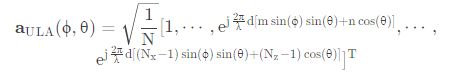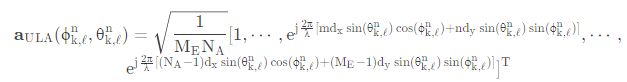mimo信道学习

1  MIMO信道

MIMO无线信道的数学模型中，是发射端第 i 根天线和接收端第 j 根天线的复信道增益，该增益来源于多条射线的叠加，每条射线是经过多条不同的路径到达接收机的

信道增益的模服从瑞利分布，如果除了大量的散射体还有一个很强的直射LoS路径，则信道增益的模服从莱斯分布

是发射端第 i 根天线和接收端第 j 根天线之间的子信道，也是由一堆不同的路径叠加而成的，而不是仅指一条路径！

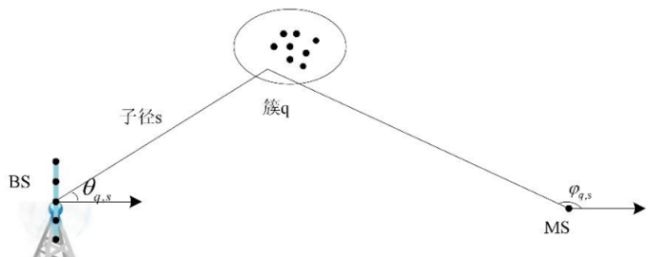
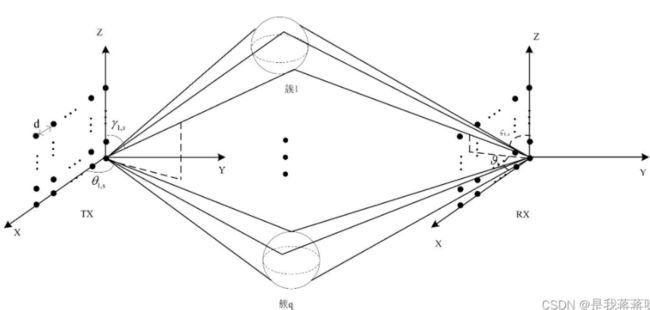
      毫米波相关论文最常使用的毫米波信道模型都是基于Saleh-Valenzuela模型，包含一堆方位角、俯仰角之类。毫米波绕射能力差，路径稀疏，信道模型具有丰富的几何特征。

      毫米波信道与低频信道不同，由于毫米波基本沿直线传播，绕射能力差，其信道的散射路径较少，往往远少于发射和接收天线的数量，因此其信道模型具有丰富的几何特征。而低频信道由于散射路径丰富，往往建模成随机信道比如瑞利分布，因此并不包含通信环境的信息。

2  均匀线性阵列（Uniform Linear Array, ULA）

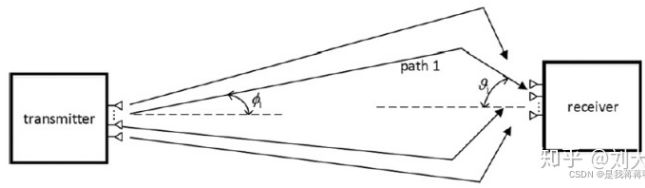
     2D MIMO 通信系统发射天线是线性天线，它形成的波束较宽，只有水平维度的方向，没有垂直维度的方向。这样每条子径包含发射端的出发角 AoD（Angle of Departure），接收端的到达角 AoA（Angle of Arrival）以及时延 三个特征变量。

3 均匀平面阵列（Uniform Planar Array, UPA） 

3D MIMO 通信系统一般在基站端配备大规模的均匀平面天线阵列 。3D MIMO 通信系统基站端配备的天线元件多，且相对于 2D MIMO 通信系统新增加了垂直方向的天线自由度，即系统可以同时在水平维和垂直维上灵活精确调整波束方向，这样发射端可以形成更窄、更精确的波束，具有很高的指向性。 此时描述子径的应该是离开和到达的方位角，仰角

 

 

4 毫米波信道模型

 （1）发射端和接收端均采用ULA

假设只有 L 条散射路径。经典的 Saleh-Valenzuela (S-V) 信道模型，假设发射天线有

根，接受天线有根，则L条散射路径的归一化窄带毫米波信道可以表示为：

 代表第 ℓ 条路径的衰落系数，一般建模为高斯分布。

 分别是第 ℓ 条路径的到达角 AoA 和出发角 AoD，一般简化假设在内均匀分布。

 是天线阵列的方向矢量(steering vector)，又称为 array response，当天线为 N 维 ULA 时，归一化的方向矢量表达式为：

   表示的是第 ℓ 径接收端的方向矢量，是维的向量；表示第 ℓ  径的发射端的方向矢量，是 维的向量;

维的矩阵; 把这些所有 L条路径相加，也就是我们的信道矩阵。

MIMO信道收发端都是 ULA天线阵列的时候，steering vector（方向矢量）如上所示，但对于 MISO (SIMO) 模型，接收端（发射端）只有一个天线的话应该就不用考虑接收端（发射端）的方向矢量了。

 

（2）发射端和接收端均为 UPA

假设有 个散射簇，每个散射簇中包含条传播路径。窄带毫米波信道表示为：

 代表第i个散射簇中第 ℓ 条路径的衰落系数。

 代表接收端的方向角和俯仰角。表示方向角和俯仰角在接收端的归一化天线阵列响应向量。

 代表发射端的方向角和俯仰角,表示方向角和俯仰角在发射端的归一化天线阵列响应向量。

 针对该图 UPA放置在 X-Z 平面上的情形，发射端 UPA天线阵列的归一化响应向量可以表示为

 N 为均匀平面阵列的天线元素个数，x 轴和 z 轴上分别有个天线元素,d 是天线间隔。该表达式还可以写为克罗内克积的形式，更简洁。

 针对UPA来说，steering vector 和俯仰角的关系取决于UPA的在三维坐标中的放置，下面给出 UPA 放置在Y-Z平面 和 X-Y平面的两种情形。(IRS放置不同对信道估计的影响)

X-Y平面放置IRS的情形:   

UAV 端的 UPA 天线阵列的归一化响应向量 [5] 可以表示为：

 分别表示X和Y轴上的天线之间的间距，一般取 d = 0.5λ 

 毫米波信道学习记录_Dr. Wenny的博客-CSDN博客_毫米波信道

代码实现：

• 实现单侧UPA的天线响应向量的仿真函数

function y = array_response(phi,theta, N)  
for m= 0:sqrt(N)-1     % IRS is square array (N elements)
    for n= 0:sqrt(N)-1
        y(m*(sqrt(N))+n+1) = exp( 1i* pi* ( m*sin(phi)*sin(theta) + n*cos(theta) ) ); % 各个方向的角度的响应用矩阵表示
    end
end
y = y.'/sqrt(N);         % 取共轭转置
end
 

• BS-IRS 信道生成函数 （IRS - UE的信道生成同理）

function H = generate_channel(Nt, Nr, L)
    AoD = pi*rand(L, 2) - pi/2;  % -2/pi~2/pi (generating the angles of departure for L paths)
    AOA = pi*rand(L, 2) - pi/2;  % -2/pi~2/pi (generating the angles of arrival for L paths)
    alpha(1) = 1;                  % gain of the LoS
    alpha(2:L) = 10^(-0.5)*(randn(1,L-1)+1i*randn(1,L-1))/sqrt(2);  % gains of the NLoS
    H = zeros(Nr, Nt);
for l=1:1:L
    ar = array_response(AOA(L,1),AOA(L,2), Nr);
    at = array_response(AOD(L,1),AOD(L,2), Nt);
    H = H + sqrt(Nr * Nt)*alpha(l)*ar*at';
end