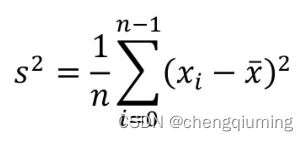KD 树原理详解

一 点睛

KD 树（K-Dimension tree）是可以存储 K 维数据的树，是二叉搜索树的拓展，主要用于多维空间数据的搜索，例如范围搜索和最近邻搜索。BST、AVL、Treap 和伸展树等二叉搜索树的节点存储的都是一维信息，一维数据很容易处理，直接比较数据的大小，满足左子树小于根、右子树大于根即可。多维数据需要选择一个维度 Di，在维度 Di 上进行大小比较。例如，对于二维平面上的两个点 A(2,4)、B(5, 3)，按照第 1 维比较，则 AB。

二 创建 KD 树

KD 树是二叉树，表示对 K 维数据的划分，每个节点都对应 K 维空间划分中的超矩形区域，KD 树可以省去大部分的搜索工作，提高搜索效率。

对 K 维数据划分左右子树时，需要考虑两个问题：

① 选择哪个维度划分？

② 选择哪个划分点可以使左右子树的大小大致相等？

众所周知，二叉搜索树在极不平衡的情况下退化为线性，效率最差，在平衡的情况下时间复杂度为 O(logn)。

1 维度划分

维度划分指选择哪一维进行划分，即选择哪一维作为分辨器。KD 树可以根据不同的用途选择不同的分辨器，最常见的是轮转法和最大方差法。

• 轮转法

按照维度轮流作为分辨器，对于二维数据(x , y)，第 1 层按 x 划分，第 2 层按 y 划分，第 3 层按 x 划分，以此重复进行。奇数层按 x 划分，偶数层按 y 划分，按照维度轮流划分，创建一棵 KD 树。如同切豆腐块，竖着切一刀，横着切一刀，以此重复进行。扩展到 K 维数据，若当前层按照第 i 维划分，则下一层按照第(i +1) % K 维划分，i=0,1,…, K-1。

最大方差法：若数据在维度D i 上方差最大，则选择维度D i

• 最大方差法

若数据在维度 Di 上方差最大，则选择维度 Di 作为分辨器。方差公式为：

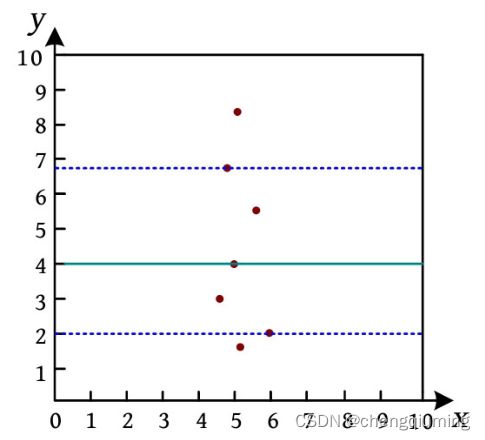
其中，x 为所有 xi 的平均数。方差用于反映数据的波动大小（即分散程度），方差越大，分散得越开，越容易划分。例如，二维数据如下图所示，数据在 x 维度方差较小，在 y 维度方差较大，按照 y 维度划分更好一些。

2 选择划分点

为了保障左右子树大致相等，可以将中位数作为划分点。

三 图解

给定一个二维数据集：A(2,3)、B(5,4)、C(9,6)、D(4,7)、E(8,1)、F(7,2)，构建一棵 KD 树。

以轮转法为例，构建过程如下。

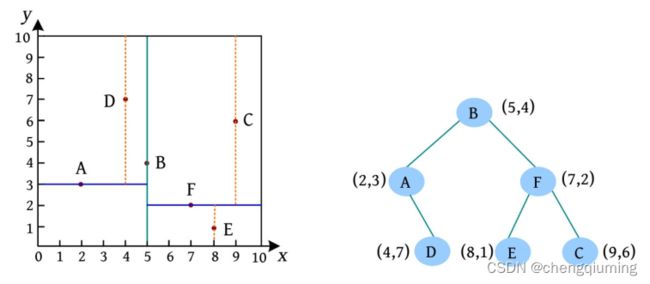
1 第 1 层按照第 1 维 x 划分，6 个 点的 x 值分别为2、4、5、7、8、9，按中位数 5 一分为二，像切豆腐块一样，在 x=5 的位置竖着切一刀。将划分点 B(5, 4) 作为 KD 树的根，左侧两个点为 A、D，右侧三个点为 C、E、F。

2 第 2 层再按照第 2 维 y 划分，左侧两个点的 y 值分别为 3、7，A 作为左子树的树根；右侧三个点的 y 值分别为 1、2、6，按中位数 2 一分为二，将 F 作为右子树的树根。

3 就这样一直进行下去，直到左右两侧没有数据为止。

二维切分图和对应的 K D树如下图所示。

四 m 近邻搜索

在 KD 树中查询给定目标点 p 最近邻的 m 个点，首先从根节点出发，向下递归，若点 p 当前维的坐标小于树根，则在左子树中查询，否则在右子树中查询。在查询过程中用优先队列（最大堆）存储最近邻的 m 个点，当存在某一点 q 比优先队列中的最远点距离 p 更近时，优先队列堆顶出队，q 入队。

在以下两种情况下，需要继续在当前划分点的另一区域查询。

• 在优先队列中存储的最近邻点不足 m 个；

• 以 p 为球心且 p 到最近邻点（m 个最近邻点中的最远点）的距离为半径的超球体与划分点的另一个区域相交。

五 图解

假设有一棵 KD 树包含 6 个点 A(2, 3)、B(5, 4)、C(9, 6)、D(4,7)、E(8, 1)、F(7, 2)，需要查询离 p(6, 6) 最近的两个点。

查询过程如下。

1 当前维度为 x ，p 的 x 坐标大于树根 B，在B的右子树中查询。

2 当前维度为 y ，p 的 y 坐标大于树根 F，在 F 的右子树中查询。

3 当前维度为 x ，p 的 x 坐标小于树根 C，在 C 的左子树中查询。

4 C 的左子树为空，优先队列元素个数小于2，C 入队。

5 C 的右子树为空，返回到 F，优先队列的元素个数小于2，F 入队，搜索 F 的左子树。

6 F的左子树 E 到 p 的距离比队列中的最远点大，无须入队。

7 返回到 B，B 到 p 的距离比队列中的最远点小，F 出队，B入队。

8 以 p 为球心 且 p 到队列中最远点的距离为半径的超球体与划分点 B 的另一区域有交集（d

9 在 B 的左子树中，D 到 p 的距离比队列中的最远点小，C 出队，D 入队。

10 距离 p 点最近的两个点为 D、B。

欧几里得距离又叫作欧氏距离，常用作两点之间的距离度量。点 p 和点 q 之间的欧氏距离是连接它们的直线段的长度。在笛卡尔坐标系中，若p =(p1 , p2 , …, pn )和q =(q1 , q2 , …, qn ) 是 N 维空间中的两点，则 p 、q 的欧氏距离为 

这里只是求给定目标点 p 最近邻的 m 个点，因此不需要开方，只求平方和即可比较大小。