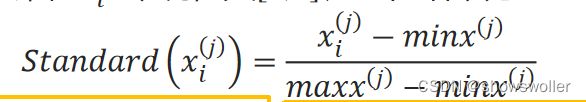【Python机器学习】Sklearn库中Kmeans类、超参数K值确定、特征归一化的讲解(图文解释)
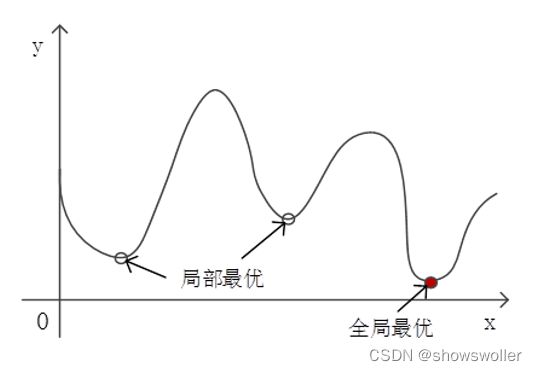
一、局部最优解
采用随机产生初始簇中心 的方法,可能会出现运行 结果不一致的情况。这是 因为不同的初始簇中心使 得算法可能收敛到不同的 局部极小值。
不能收敛到全局最小值,是最优化计算中常常遇到的问题。有一类称为凸优化的优化计算,不存在局部最优问题。凸优化是指损失函数为凸函数的最优化计算。在凸函数中,没有局部极小值这样的小“洼地”,因此是最理想的损失函数。如果能将优化目标转化为凸函数,就可以解决局部最优问题。
二、Sklearn库中的Kmeans类
kmeans类中参数和方法如下
class sklearn.cluster.KMeans(n_clusters=8, init=’k-means++’, n_init=10, max_iter=300, tol=0.0001, precompute_distances=’auto’, verbose=0, random_state=None, copy_x=True, n_jobs=None, algorithm=’auto’)
fit(X[, y, sample_weight]) # 分簇训练
fit_predict(X[, y, sample_weight]) # 分簇训练并给出每个样本的簇号
predict(X[, sample_weight]) # 在训练之后,对输入的样本进行预测
transform(X) # 计算样本点X与各簇中心的距离
1)init参数
KMeans类通过init参数提供了三种设置初始簇中心的方法,分别为k-means++、random和用户指定。KMeans类通过init参数提供了三种设置初始簇中心的方法,分别为k-means++、random和用户指定。
random是由算法随机产生簇中心。
用户指定是通过一个ndarray数组将用户设置好的初始簇中心传入算法。
2)n_init参数
n_init参数指定算法重复运行次数。通过多次重复运行算法,最终选择最好的结果作为输出。
3)max_iter参数和tol参数
max_iter参数和tol参数是迭代的退出条件。
max_iter参数指定一次运行中的最大迭代次数,达到最大次数时结束迭代。
tol参数指定连续两次迭代变化的阈值,如果损失函数的变化小于阈值,则结束迭代。
三、超参数K值的确定
可以对不同的k值逐次运行算法,取“最好结果”。要注意的是,这个“最好结果”并非是SSE等算法指标,而是要根据具体应用来确定。
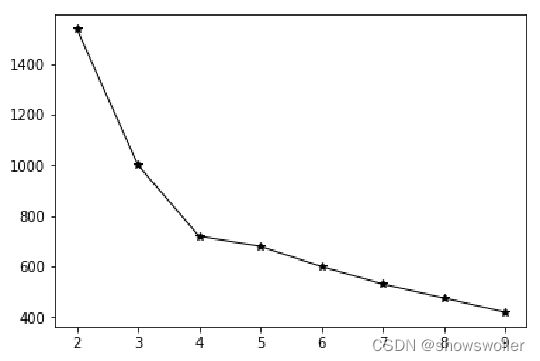
通常用拐点法又称肘部法来确定
如下图所示 当图像出现拐点的值选取为K值比较合适,下图即为4或者5
四、特征归一化
k-means算法对样本不同特征的分布范围非常敏感。
已知小明(160,60000),小王(160,59000),小李(170,60000)。根据常识可以知道小明和小王体型相似,但是如果根据欧氏距离来判断,小明和小王的距离要远远大于小明和小李之间的距离,即小明和小李体型相似。这是因为不同特征的度量标准之间存在差异而导致判断出错。
为了使不同变化范围的特征能起到相同的影响力,可以对特征进行归一化(Standardize)的预处理,使之变化范围保持一致。常用的归一化处理方法是将取值范围内的值线性缩放到[0,1]或[-1,1]。
对第j个特征x^(j)来说,如果它的最大值和最小值分别是maxx^(j)和minx^(j),则对于某值x_i^(j)来说,其[0,1]归一化结果为:
Sklearn的prepeocessing模块提供了一些通用的对原始数据进行特征处理的工具。
from sklearn.preprocessing import MinMaxScaler
import numpy as np
#对数据进行归一化
X = np.array([[ 0., 1000.],
[ 0.5, 1500.],
[ 1., 2000.]])
min_max_scaler = MinMaxScaler()
X_minmax = min_max_scaler.fit_transform(X)
X_minmax
>>>array([[0. , 0. ],
[0.5, 0.5],
[1. , 1. ]])
# 将相同的缩放应用到其它数据中
X_test = np.array([[ 0.8, 1800.]])
X_test_minmax = min_max_scaler.transform(X_test)
X_test_minmax
>>>array([[0.8, 0.8]])
# 缩放因子
min_max_scaler.scale_
>>>array([1. , 0.001])
# 最小值
min_max_scaler.min_
>>>array([ 0., -1.])
创作不易 觉得有帮助请点赞关注收藏~~~