基于深度学习的大规模vSLAM场景中的鲁棒视觉位置识别

Towards a Robust Visual Place Recognition in Large-Scale vSLAM Scenarios Based on a Deep Distance Learning

关键字：视觉位置识别、vSLAM、深度学习、多约束损失、CNN

---

---

一、摘要和总结

虽然使用卷积神经网络能够实现比手工制作的特征描述符更好的性能，但是视觉位置识别会受到两个主要的问题影响：

1. 感知混叠
2. 感知可变性

因此设计一个定制的距离学习方法来代表在大规模vSLAM场景中的固有距离约束是至关重要的。传统的深度距离学习方法通常是使用triplet loss，但是这可能导致冗余的低效的训练和异常的距离关系，这篇文章对于视觉位置识别提出了一个新颖的深度距离学习框架，通过深入分析视觉位置识别问题中距离关系的多重约束，提出了在欧几里得空间优化距离约束关系的多约束损失。新框架可以支持任何类型的 CNN，如 AlexNet、VGGNet 和其他用户定义的网络，以提取更多有区别的特征。

二、框架和方法

这篇文章其实就是使用通用的CNN模型，然后使用提出的多约束深度距离学习方法来训练网络，使其能够进行位置识别任务。对于网络提取出来的特征向量，通过比较两个特征向量之间的欧式距离来计算相似度。其主要的目的是提升CNN模型的特征提取能力，核心就需要网络能够提取出来更易于辨别的特征描述符。因为框架可以支持任意一种已知的CNN网络，这里选用了AlexNet和VGGNet作为两个实例来展示多约束深度距离学习。框架图如下所示

我们使用连续的多帧图像组合 作为输入而不是使用单帧图像来获得他们的低维特征向量，这样欧氏距离就可以直接用来度量不同位置的相似性，如果欧式距离低于一个阈值，那么我们就可以提出一个位置识别假设，这阈值是提前人为设置的，这篇文章当中是使用具有最好精度的最大召回率作为阈值

基于CNN的图像特征提取

全连接层可以作为特征提取器来获得特征向量，不同层提取出来的特征表现出来不同的性能，实验证明顶层的泛化能力是要低于更低层的，值得注意的是，在我们的研究中，AlexNet和VGGNet的架构被简化用于视觉位置识别问题，把原始的全连接层改为定制的可调节尺寸的全连接层，这个全连接层是作为特征提取器来编码具有可调节向量长度的从深度距离学习方法中学到的特征描述。

Triplet loss

标准的triplet loss方法，三张图像会组合为一个元组，$i,j,k$是从图像数据集中挑选出来的图像序列号，要组成合适的元组需要满足以下条件：

1. 图像$i$和图像$j$来自相同的分类但不是相同的图像
2. 图像$i$和图像$k$来自不同的分类

考虑一个元组如$(x^a,x^p,x^n)$，这里面$x^a$和$x^p$来自于相同的分类，$x^a$和$x^n$来自于不同的分类。triplet loss函数的目的是去优化CNN网络来学习图像$x$的描述$f(x)$，关于输入元组$(x^a,x^p,x^n)$理想的图像描述应该满足如下的距离关系：
$${\Vert f(x_a-f(x_p))\Vert }_2^2+\alpha \le {\Vert f(x_a-f(x_n))\Vert }_2^2$$其中$\alpha$是相同类和不同类图像对之间的幅度值，所有特征向量都约束在超球面${\Vert f(x)\Vert }_2=1$中，来避免损失超出0。通常这个损失定义为：
$$L_{tri}(x^a,x^p,x^n)=max\left\{{\Vert f(x_a-f(x_p))\Vert }_2^2+\alpha -{\Vert f(x_a-f(x_n))\Vert }_2^2,0\right\}$$训练的目标是去学习一个可辨别的图像描述，也就是$x^a和x^p$的距离最小化，$x^a和x^n$的距离最大化，虽然之前使用triplet loss以及它的一些改进，在不同任务上取得了相当不错的效果，但是还是有一些缺点需要去改进。为了最大化在每一个元组中匹配的和没匹配的图像对之间的距离 ，可能会导致图下图所示的异常的距离关系，定义一个$dict()$函数来表示特征向量之间的欧式距离，为了优化这个元组，我们在最大化$dict(f(x^a),f(x_1^n))$可能会导致$dict(f(x_1^n),f(x_2^n))$变小，但是图像1和图像2很可能来自不同的位置。所以针对于这个问题，提出了多约束损失

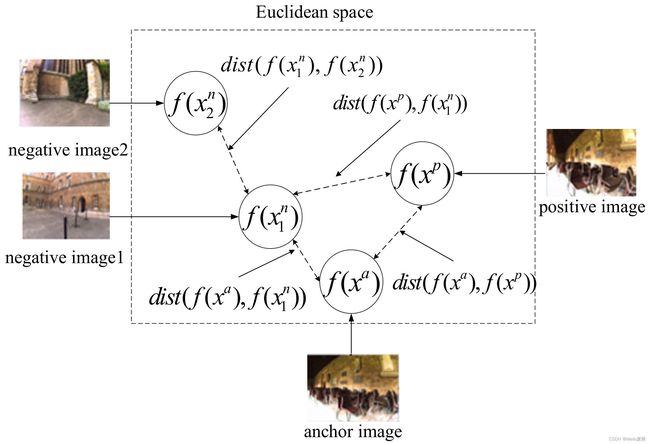
多约束损失

对于triplet loss，其只会考虑两方面的距离关系：一个是$f(x^a)和f(x^p)$之间的距离，另一个是$f(x^a)和f(x^n)$之间的距离，不同于triplet loss，这篇文章创建了多约束图像集$X=(X^p,X^n)$，而不是像之前的元组作为输入，每一个多约束图像集都会包含两个不同的图像集：positive图像集:$X^p=(X_1^p,\dots ,X_A^p)$包含来自相同位置的图像和negative图像集:$X^p=(X_1^n,\dots ,X_B^n)$包含来自不同位置的图像。假设来自同一地点的图像彼此靠近，不同地点的图像应该在特征空间中应该相隔很远。多约束损失图如下图所示

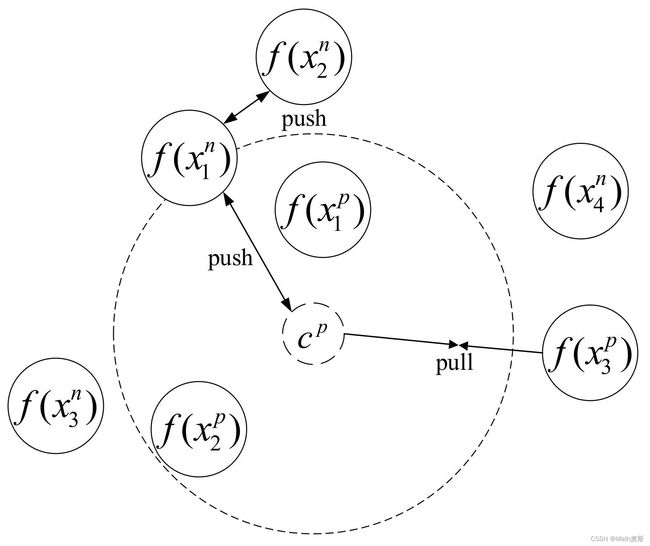
$c^p$ 代表在positive图像集的图像中心点，由如下的公式计算
$$c^p=\frac{1}{A}\sum _{i=1}^{A}f(x_i^p)$$不同于triplet loss，多约束损失会约束三方面的距离关系：positive图像和中心点之间的距离关系(DR1)；另一个是negative图像和中心点之间的距离关系(DR2)；最后一个是在negative图像集中的图像之间的距离关系(DR3)
对于一个多约束图像集$X=(X^p,X^n)$，关于期望的 DR1 和 DR2 的距离应该满足如下的状态
∥ f ( x i p − c p ) ∥ 2 2 + α ≤ ∥ f ( x j n ) − c p ∥ 2 2 , ∀ 1 ≤ i ≤ A a n d 1 ≤ j ≤ B \left \|f(x_{i}^{p}-c^{p})\right \|_{2}^{2}+\alpha\leq\left \|f(x_{j}^{n})-c^{p}\right \|_{2}^{2},\forall1\leq i \leq A and 1 \leq j \leq B ∥f(xip​−cp)∥22​+α≤ ​f(xjn​)−cp ​22​,∀1≤i≤Aand1≤j≤B这里面的 $\alpha$ 是预先定义的超参数。与此同时，为了解决triplet loss存在的问题，也就是去最大化 $dict(f(x_j^n,f(x_k^n)))$，根据三角形的距离关系，我们必须满足DR1和DR3之间的以下约束
∥ f ( x i p − c p ) ∥ 2 2 + β ≤ ∥ f ( x j n ) − f ( x ∗ n ) ∥ 2 2 , ∀ 1 ≤ i ≤ A a n d 1 ≤ j ≤ B \left \|f(x_{i}^{p}-c^{p})\right \|_{2}^{2}+\beta\leq\left \|f(x_{j}^{n})-f(x_{*}^{n})\right \|_{2}^{2},\forall1\leq i \leq A and 1 \leq j \leq B ∥f(xip​−cp)∥22​+β≤ ​f(xjn​)−f(x∗n​) ​22​,∀1≤i≤Aand1≤j≤B $\beta$ 和 $\alpha$ 同理，$x_{\ast }^n$ 可以从negative图像集中随机选择但 $x_{\ast }^n$ $\ne$ $x_j^n$，像之前说的，$X^n$ 中的每个位置只有一个图像。因此，$x_{\ast }^n$ 和 $x_j^n$ 是来自不同的位置的。
在一个多约束的图像集中，距离约束可以转化为如下所示的最小化的问题
L m u l t i ( X p , X n ) = m a x { 0 , ∥ f ( x i p ) − c p ∥ 2 2 + α − ∥ f ( x j n ) − c p ∥ 2 2 } + m a x { 0 , ∥ f ( x i p − c p ) ∥ 2 2 + β − ∥ f ( x j n ) − f ( x ∗ n ) ∥ 2 2 } , ∀ 1 ≤ i ≤ A a n d 1 ≤ j ≤ B L_{multi}(X^{p},X^{n})=max\left \{0,\left \| f(x_{i}^{p})-c^{p}\right \|_{2}^{2}+\alpha-\left\| f(x_{j}^{n})-c^{p}\right \|_{2}^{2} \right \}\\ +max\left \{ 0,\left \| f(x_{i}^{p}-c^{p})\right \|_{2}^{2}+\beta-\left\| f(x_{j}^{n})-f(x_{*}^{n})\right \|_{2}^{2}\right \},\forall1\leq i \leq A and 1 \leq j \leq B Lmulti​(Xp,Xn)=max{0,∥f(xip​)−cp∥22​+α− ​f(xjn​)−cp ​22​}+max{0,∥f(xip​−cp)∥22​+β− ​f(xjn​)−f(x∗n​) ​22​},∀1≤i≤Aand1≤j≤B但如果多约束图像集较大，则优化过程将太耗时，无法在嵌入式系统中执行，加快这一进程，我们首先从 $c^p$ 中通过 ${\max }_i({\Vert f(x_i^p-c^p)\Vert }_2^2),i=1,2,...,A$ 找到最远的positive图像$x_{farthest}^p$，然后再通过 max ⁡ i ( ∥ f ( x j n − c p ) ∥ 2 2 ) , j = 1 , 2 , . . . , B \max_{i}(\left \| f(x_{j}^{n}-c^{p})\right \|_{2}^{2}),j=1,2,...,B maxi​( ​f(xjn​−cp) ​22​),j=1,2,...,B 找到最近的negative图像$x_{nearest}^n$。因此，损失函数可以简化为
L m u l t i ( X p , X n ) = m a x { 0 , ∥ f ( x f a r t h e s t p ) − c p ∥ 2 2 + α − ∥ f ( x n e a r e s t n ) − c p ∥ 2 2 } + m a x { 0 , ∥ f ( x f a r t h e s t p ) − c p ∥ 2 2 + β − ∥ f ( x n e a r e s t n ) − f ( x ∗ n ) ∥ 2 2 } , ∀ 1 ≤ i ≤ A a n d 1 ≤ j ≤ B L_{multi}(X^{p},X^{n})=max\left \{0,\left \| f(x_{farthest}^{p})-c^{p}\right \|_{2}^{2}+\alpha-\left\| f(x_{nearest}^{n})-c^{p}\right \|_{2}^{2} \right \}\\ +max\left \{ 0,\left \| f(x_{farthest}^{p})-c^{p}\right \|_{2}^{2}+\beta-\left\| f(x_{nearest}^{n})-f(x_{*}^{n})\right \|_{2}^{2}\right \},\forall1\leq i \leq A and 1 \leq j \leq B Lmulti​(Xp,Xn)=max{0, ​f(xfarthestp​)−cp ​22​+α−∥f(xnearestn​)−cp∥22​}+max{0, ​f(xfarthestp​)−cp ​22​+β−∥f(xnearestn​)−f(x∗n​)∥22​},∀1≤i≤Aand1≤j≤B因此，多约束损失可以学习有效的特征描述，该特征描述可以满足视觉位置识别中的相对距离关系，并且可以使
提取的特征更具辨别性。中心点 $c^p$ 代替选择anchor图像来约束positive图像和negative图像整体的距离关系。此外，多约束图像集的构建保证了来自同一地点的所有图像都将移动到更靠近中心点 $c^p$ 的位置。因此，positive图像和negative图像之间的整体距离关系可以通过聚类方法导出的中心点 $c^p$ 来测量和约束。在原始的元组生成方法中，训练过程效率低下，这可能会给实时自主机器人中视觉位置识别的部署使用带来计算负担。因此，引入了多约束图像集的思想，可以保证基于“图像位置”的更快的训练和测试过程。它有助于所提出的方法处理连续帧，这可以加快测试过程。

创建多约束图像集

现存的视觉位置识别任务的数据集通常包含图像和真值标签，我们使用相同的标签标记相同的位置，对于第k个位置包含u张图片，如果满足如下的距离关系，我们就会增加图像 $x_i$ 到临时positive图像集 $X_{tem}^p$ 中
$${\Vert f(x_i)-c^p\Vert }_2^2>\gamma ,\forall 1\le i\le u$$而对于其他位置，比如第t个位置，如果距离关系满足如下的式子，我们增加图像 $x_j$ 到临时的negative图像集 $X_{tem}^n$ 中
$${\Vert f(x_j)-c^p\Vert }_2^2<{\gamma }_{{}^{\prime }},\forall 1\le j\le v$$因此我们通过算法1创建合适的多约束图像集，在训练集中的每一张图像都有一个相关的位置标签，每一个位置所包含的图像数量是不固定的。首先，我们遍历每个图像并计算该图像所属位置的中心点，之后会按照距离关系构建一个临时的positive图像集 $X_{tem}^p$ 和一个临时的negative图像集 $X_{tem}^n$，然而 $X_{tem}^p$ 和 $X_{tem}^n$ 的长度没有必要和通过 $X^p$ 和 $X^n$ 定义的输入的长度匹配，因此，我们可以将 $X_{tem}^p$ 和 $X_{tem}^n$ 的长度分别调整为A和B。

训练过程

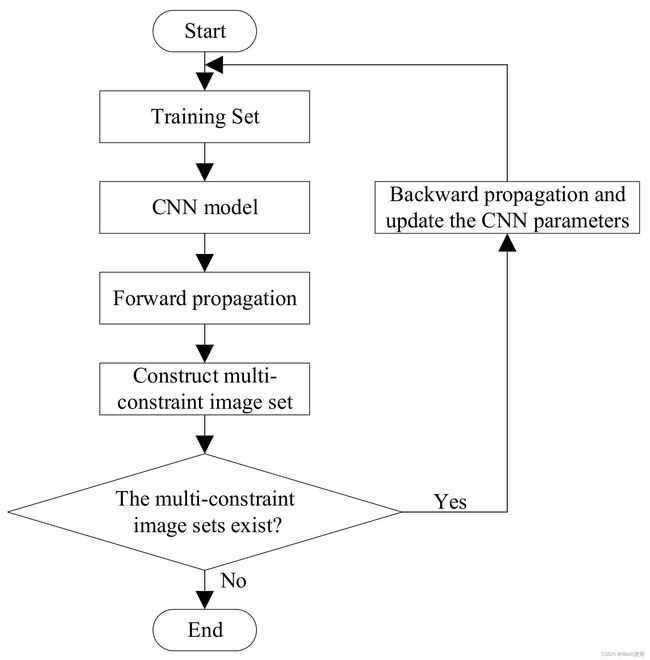
首先，我们将训练集分成大小为（A+B）的几个小批量。这些小批量被输入到共享由多约束损失函数更新参数的CNN模型中。通过这种方式，可以通过前向传播导出每个图像的特征向量。然后，我们可以根据算法1构造合适的多约束图像集。如果存在多约束图像集合，我们将使用多约束损失函数更新CNN模型的参数。如果不存在任何多约束图像集，则训练过程结束，这意味着CNN已成功训练。

小结

以上是关于这篇论文方法部分的基本介绍，可能有遗漏的部分或者是没有理解对的地方，欢迎大家及时指正。