《深度学习入门》笔记(一)
《深度学习入门1》笔记(一)
神经网络的传播
如下图,我们把最左边的一列称为输入层,最右边的一列称为输出层,中间的一列称为中间层,也称为隐藏层。“隐藏”一词的意思是,隐藏层的神经元(和输入层、输出层不同)肉眼看不见。另外,把输入层到输出层依次称为第0 层、第1 层、第2 层(层号之所以从0 开始,是为了方便后面基于Python 进行实现)。
- 前向传播(forward propagation)
信号自输入层经若干中间层至输出层的过程为前向传播,如图所示:
-
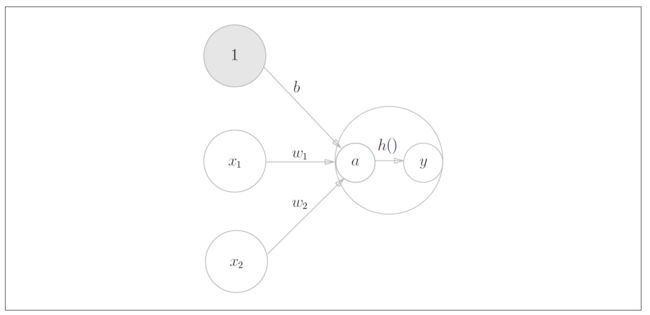
Affine
Affine层在卷积神经网络中称为全连接层,层的各输出分别与每个输入相连接,输入到输出的映射关系称为仿射变换(一次线性变换和一次平移)。若以 x \bm{x} x表示输入,以 a \bm{a} a表示输出,则有
a = x W + b \bm{a} = \bm{xW} + \bm{b} a=xW+b
其中 W \bm{W} W和 b \bm{b} b是参数, W \bm{W} W为权重, b \bm{b} b为偏移量。 -
激活函数
激活函数 h ( ) h() h() 的作用在于决定如何激活输入信号的总和
计算加权输入信号和偏置的总和,记为 a {a} a ;用 h ( ) h() h() 函数将 a {a} a 转换为输出 y {y} y
常见的激活函数有:
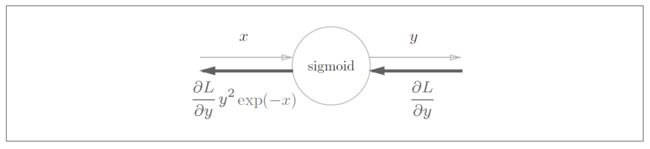
- s i g m o i d sigmoid sigmoid 函数
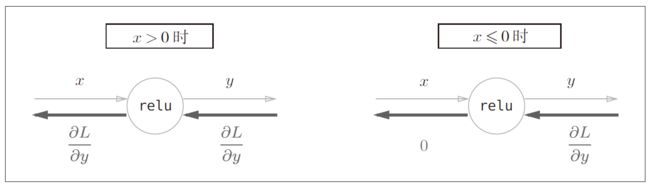
h ( x ) = 1 1 + e − x h(x) = \frac{1}{1+e^{-x}} h(x)=1+e−x1 - R e L U ReLU ReLU 函数
h ( x ) = { x , x > 0 0 , x ≤ 0 h(x) = \left\{ \begin{aligned} x&, &x& > 0 \\ 0&, &x& \le 0 \end{aligned} \right. h(x)={x0,,xx>0≤0 - t a n h tanh tanh函数
h ( x ) = s i n h ( x ) c o s h ( x ) = e x − e − x e x + e − x h(x) = \frac{sinh(x)}{cosh(x)} = \frac{e^x - e^{-x}}{e^x + e^{-x}} h(x)=cosh(x)sinh(x)=ex+e−xex−e−x
- softmax
对于分类问题,比如手写数字识别,我们最后要判断输入数据所属的类, s o f t m a x ( ) softmax() softmax() 可以给出数据属于某个类的“概率”(不是真的概率,但可以指示概率大小)。表达式如下:
y k = e x p ( a k − m a x ( a 1 , a 2 , . . . , a n ) ) ∑ i = 1 n e x p ( a i − m a x ( a 1 , a 2 , . . . , a n ) ) y_k = \frac{exp(a_k - max(a_1,a_2,...,a_n))}{\sum_{i=1}^{n} exp(a_i - max(a_1,a_2,...,a_n))} yk=∑i=1nexp(ai−max(a1,a2,...,an))exp(ak−max(a1,a2,...,an))
而回归问题用恒等函数:
y k = a k y_k = a_k yk=ak - 分类预测
s o f t m a x ( ) softmax() softmax() 可以给出“概率”,但我们想知道的是“属于哪一类”,此时应当选择最大“概率”对应的类别。使用 a r g m a x ( ) argmax() argmax() 可以取出数组中最大值的索引。例如, s o f t m a x ( ) softmax() softmax() 的 n n n个输出中,最大值为 y k y_k yk, 则分类结果是第 k k k类。 - 识别精度(accuracy)
识别精度是评价分类效果的指标,若分类正确(预测结果与标签一致)数为 T T T, 分类错误数为 F F F, 则
A c c u r a c y = T T + F Accuracy = \frac{T}{T+F} Accuracy=T+FT - 批处理
输入数据以numpy数组的形式存在,若一个数据(如一张图片)含有 m m m个元素,其shape为 ( m , ) (m,) (m,)。在实际应用中,通常将一批(batch)数据放在一起作为神经网络的输入。假设一批数据包含 n n n个数据,即batch size = n n n, 那么神经网络输入的shape为 ( n , m ) (n,m) (n,m) - 网络结构
以手写数字识别为例,其网络结构如图所示:
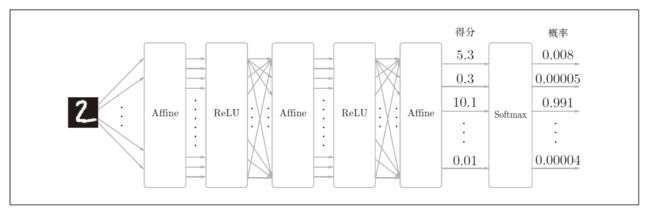
神经网络的学习
神经网络的学习指的是从训练数据中自动获取最优权重参数的过程。
- 损失函数(loss function)
在神经网络的学习中,寻找最优参数(权重和偏置)时,要寻找使损失函数的值尽可能小的参数。在进行神经网络的学习时,不能将识别精度作为指标。因为如果以识别精度为指标,则参数的导数在绝大多数地方都会变为0。
常用的损失函数有:
- 均方误差
E = 1 2 ∑ k ( y k − t k ) 2 E = \frac{1}{2} \sum_k (y_k - t_k)^2 E=21k∑(yk−tk)2
其中, y k y_k yk表示神经网络的输出, t k t_k tk 表示监督数据(以one-hot表示), k k k 表示数据的维数。 - 交叉熵误差
E = − ∑ k t k l n y k E = -\sum_k t_k\, ln\, y_k E=−k∑tklnyk
- mini-batch
所谓mini-batch就是在训练数据中取出一个batch,以batch的平均损失函数作为神经网络学习的指标,而不再以单个数据的损失函数为指标。假设一个batch有 N N N个数据, t n k t_{nk} tnk 表示第 n n n个数据的第 k k k个元素的值( y n k y_{nk} ynk 是神经网络的输出, t n k t_{nk} tnk 是监督数据)
E = − 1 N ∑ n ∑ k t n k l n y n k E = -\frac{1}{N}\sum_n \sum_k t_{nk}\, ln\, y_{nk} E=−N1n∑k∑tnklnynk - 梯度法(gradient method)
通过巧妙地使用梯度来寻找损失函数最小值(或者尽可能小的值)的方法就是梯度法。梯度表示的是各点处的函数值减小最多的方向。虽然梯度的方向并不一定指向最小值,但沿着它的方向能够最大限度地减小函数的值。在梯度法中,函数的取值从当前位置沿着梯度方向前进一定距离,然后在新的地方重新求梯度,再沿着新梯度方向前进,如此反复,不断地沿梯度方向前进。以数学式表示梯度法:
x 0 = x 0 − η ∂ f ∂ x 0 x 1 = x 1 − η ∂ f ∂ x 1 \begin{aligned} x_0 &= x_0 - \eta \frac{\partial f}{\partial x_0}\\ x_1 &= x_1 - \eta \frac{\partial f}{\partial x_1} \end{aligned} x0x1=x0−η∂x0∂f=x1−η∂x1∂f
η \eta η表示更新量,在神经网络的学习中,称为学习率(learning rate)。学习率决定在一次学习中,应该学习多少,以及在多大程度上更新参数。
神经网络的学习所说的梯度是指损失函数关于权重参数的梯度。比如,有一个只有一个形状为 2 × 3 2\times3 2×3的权重 W \bm{W} W的神经网络,损失函数用 L L L表示。此时,梯度可以用 ∂ L ∂ W \frac{\partial L}{\partial \bm{W}} ∂W∂L表示。用数学式表示的话,如下所示
W = ( w 11 w 12 w 13 w 21 w 22 w 23 ) ∂ L ∂ W = ( ∂ L ∂ w 11 ∂ L ∂ w 12 ∂ L ∂ w 13 ∂ L ∂ w 21 ∂ L ∂ w 22 ∂ L ∂ w 23 ) \begin{array}{r} \bm{W} =& \left( \begin{array}{l} w_{11} &w_{12} &w_{13} \\ w_{21} &w_{22} &w_{23} \end{array} \right) \\ \frac{\partial L}{\partial \bm{W}} =& \left( \begin{array}{l} \frac{\partial L}{\partial w_{11}} &\frac{\partial L}{\partial w_{12}} &\frac{\partial L}{\partial w_{13}}\\ \frac{\partial L}{\partial w_{21}} &\frac{\partial L}{\partial w_{22}} &\frac{\partial L}{\partial w_{23}} \end{array} \right) \end{array} W=∂W∂L=(w11w21w12w22w13w23)(∂w11∂L∂w21∂L∂w12∂L∂w22∂L∂w13∂L∂w23∂L)
- 反向传播(backward propagation)
反向传播是用于计算梯度的一种方法。实际上,反向传播是根据导数的链式法则实现的,即
∂ L ∂ W = ∂ L ∂ y ∂ y ∂ W \frac{\partial L}{\partial \bm{W}} = \frac{\partial L}{\partial \bm{y}} \frac{\partial \bm{y}}{\partial \bm{W}} ∂W∂L=∂y∂L∂W∂y
这样从后往前逐级微分的过程就是反向传播。
- 学习方法
神经网络如何学习?或者神经网络参数如何更新?寻找最优参数的过程称为“最优化(optimization)”。以下是几种常用方法:
- 随机梯度下降法(SGD)
W ← W − ∂ L ∂ W \bm{W} \gets \bm{W} - \frac{\partial L}{\partial \bm{W}} W←W−∂W∂L - Momentum
v ← α v − η ∂ L ∂ W W ← W + v \begin{array}{r} \bm{v} \gets& \alpha \bm{v} - \eta \frac{\partial L}{\partial \bm{W}} \\ \bm{W} \gets& \bm{W} + \bm{v} \end{array} v←W←αv−η∂W∂LW+v - AdaGrad
在神经网络的学习中,学习率 η \eta η的值很重要。学习率过小,会导致学习花费过多时间;反过来,学习率过大,则会导致学习发散而不能正确进行。在关于学习率的有效技巧中,有一种被称为学习率衰减(learning rate decay)的方法,即随着学习的进行,使学习率逐渐减小。实际上,一开始“多”学,然后逐渐“少”学的方法,在神经网络的学习中经常被使用。
h ← h + ∂ L ∂ W ⊙ ∂ L ∂ W ( 6.5 ) W ← W − η 1 h ∂ L ∂ W ( 6.6 ) \begin{array}{r} \bm{h} \gets& \bm{h} + \frac{\partial L}{\partial \bm{W}} \odot \frac{\partial L}{\partial \bm{W}} &(6.5) \\ \bm{W} \gets& \bm{W} - \eta \frac{1}{\sqrt{\bm{h}}} \frac{\partial L}{\partial \bm{W}} &(6.6) \end{array} h←W←h+∂W∂L⊙∂W∂LW−ηh1∂W∂L(6.5)(6.6)
和前面的SGD一样, W \bm{W} W表示要更新的权重参数, ∂ L ∂ W \frac{\partial L}{\partial \bm{W}} ∂W∂L 表示损失函数关于 W \bm{W} W的梯度, η \eta η表示学习率。这里新出现了变量 h \bm{h} h,如式(6.5) 所示,它保存了以前的所有梯度值的平方和(式(6.5)中的 ⊙ \odot ⊙表示对应矩阵元素的乘法)。然后,在更新参数时,通过乘以 1 h \frac{1}{\sqrt{\bm{h}}} h1,就可以调整学习的尺度。这意味着,参数的元素中变动较大(被大幅更新)的元素的学习率将变小。也就是说,可以按参数的元素进行学习率衰减,使变动大的参数的学习率逐渐减小。
- Adam
直观地讲,Adam就是融合了Momentum和AdaGrad的方法,既有模仿物理规则的移动,又为参数的每个元素适当调整更新步伐。
- 权重初始值
参数要进行更新,首先要有一个初始值,设定什么样的初始值,经常关系到神经网络的学习能否成功。
针对不同的激活函数,应当使用不同的权重初始值以达到更好的学习效果。 - Batch Norm
为什么Batch Norm这么惹人注目呢?因为Batch Norm有以下优点:
• 可以使学习快速进行(可以增大学习率)。
• 不那么依赖初始值(对于初始值不用那么神经质)
• 抑制过拟合(降低Dropout等的必要性)
Batch Norm以进行学习时的mini-batch 为单位,按minibatch进行正规化。具体而言,就是进行使数据分布的均值为0、方差为1 的正规化。用数学式表示的话,如下所示:
μ B ← 1 m ∑ i = 1 m x i σ B 2 ← 1 m ∑ i = 1 m ( x i − μ B ) 2 x ^ i ← x i − μ B σ B 2 + ϵ \begin{array}{l} \mu_B \gets \frac{1}{m} \sum_{i=1}^m x_i \\[3mm] \sigma_B^2 \gets \frac{1}{m} \sum_{i=1}^m (x_i - \mu_B)^2 \\[3mm] \hat x_i \gets \frac{x_i - \mu_B}{\sqrt{\sigma_B^2 + \epsilon}} \end{array} μB←m1∑i=1mxiσB2←m1∑i=1m(xi−μB)2x^i←σB2+ϵxi−μB
- 过拟合
过拟合指的是只能拟合训练数据,但不能很好地拟合不包含在训练数据中的其他数据的状态。发生过拟合的原因,主要有以下两个:
• 模型拥有大量参数、表现力强。
• 训练数据少。
- 权值衰减
权值衰减是一直以来经常被使用的一种抑制过拟合的方法。该方法通过
在学习的过程中对大的权重进行惩罚,来抑制过拟合。很多过拟合原本就是因为权重参数取值过大才发生的。
神经网络的学习目的是减小损失函数的值。这时,例如为损失函数加上权重的平方范数(L2 范数)。这样一来,就可以抑制权重变大。
L ^ = L + 1 2 λ W 2 \hat L = L + \frac{1}{2} \lambda \bm{W}^2 L^=L+21λW2
这里, λ \lambda λ是控制正则化强度的超参数。 λ \lambda λ设置得越大,对大的权重施加的惩罚就越重。此外, 开头的 1 2 \frac{1}{2} 21是用于将 1 2 λ W 2 \frac{1}{2} \lambda \bm{W}^2 21λW2的求导结果变成 λ W \lambda \bm{W} λW的调整用常量。
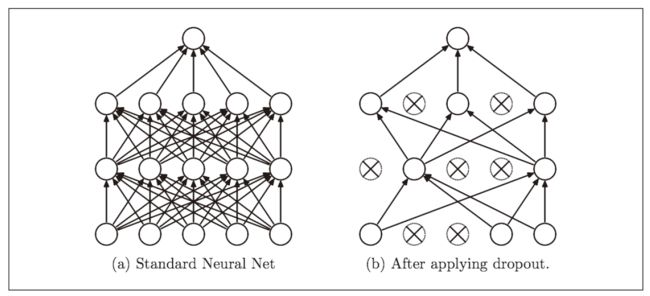
- Dropout
如果网络的模型变得很复杂,只用权值衰减难以应对过拟合。在这种情况下,我们经常会使用Dropout. Dropout 是一种在学习的过程中随机删除神经元的方法。训练时,随机选出隐藏层的神经元,然后将其删除。被删除的神经元不再进行信号的传递。
- 超参数
这里所说的超参数是指,比如各层的神经元数量、batch 大小、参数更新时的学习率或权值衰减等。如果这些超参数没有设置合适的值,模型的性能就会很差。超参数最优化步骤如下:
步骤0
设定超参数的范围。
步骤1
从设定的超参数范围中随机采样。
步骤2
使用步骤1 中采样到的超参数的值进行学习,通过验证数据评估识别精度(但是要将epoch 设置得很小)。
步骤3
重复步骤1 和步骤2(100 次等),根据它们的识别精度的结果,缩小超参数的范围。
反复进行上述操作,不断缩小超参数的范围,在缩小到一定程度时,从该范围中选出一个超参数的值。这就是进行超参数的最优化的一种方法。
[日]斋藤康毅 著,陆宇杰 译,深度学习入门:基于Python的理论与实现 ↩︎