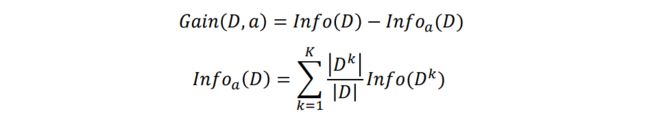机器学习——03决策树算法
机器学习——03决策树算法
参考资料
- AIlearning
- Machine-Learning-in-Action
- 庞善民.西安交通大学机器学习导论2022春PPT
具体算法的原理步骤请参考本人的另一篇博文：[机器学习导论]—— 第四课——决策树
一、信息熵与信息增益
信息熵
信息熵使信息得以量化
1948年，香农(ClaudeShannon)在他著名的论文“通信的数学原理”中指出：“信息是用来消除随机不确定性的东西”，并提出了“信息熵”的概念（借用了热力学中熵的概念），来解决信息的度量问题。
一条信息的信息量和它的不确定性有着直接的关系
比如，要搞清楚一件非常不确定的事，或是我们一无所知的事情，就需要了解大量信息。相反，如果我们对某件事已经有了较多了解，那么不需要太多信息就能把它搞清楚
信息熵是消除不确定性所需信息量的度量，也即未知事件可能含有的信息量。需要引入消除不确定性的信息量越多，则信息熵越高，反之则越低。
例如“中国男足进军2022年世界杯决赛圈”，这个因为确定性很高，几乎不需要引入信息，因此信息熵很低。
信息熵的计算
Shannon定义的信息熵的计算公式如下：
其中X表示随机变量，随机变量的取值为{1,2,…,}，()表示事件发生的概率，且有 ∑ ( ) = 1 \sum()=1 ∑P(xi)=1。信息熵的单位为比特（bit）
熵越小表示概率分布的纯度越高，反之，熵越大表示概率分布的纯度越低。
数据集的信息熵
设数据集D中有m个不同的类C1,C2,C3,…,Cm
设Di是数据集D中Ci类的样本的集合,|D|和|Di|分别是D和Di中的样本个数
数据集D的信息熵
I n f o ( D ) = − ∑ i = 1 m p i log 2 p i Info(D)=-\sum^m_{i=1}p_i\log_2p_i Info(D)=−i=1∑mpilog2pi
其中是数据集D中任意样本属于类Ci的概率，用 ∣ D i ∣ ∣ D ∣ \frac{|D_i|}{|D|} ∣D∣∣Di∣估计
使用熵衡量数据纯度
假设有一个数据集合D，其中只有两个类，一个是正例类，一个是负例类。计算D中正例类和负例类在三种不同的组分下熵的变化情况。
（1）D中包含有50%的正例和50%的负例。
I n f o ( D ) = − 0.5 ∗ log 2 0.5 − 0.5 ∗ log 2 0.5 = 1 Info(D) = -0.5 * \log_20.5 - 0.5 * \log_20.5 = 1 Info(D)=−0.5∗log20.5−0.5∗log20.5=1
（2）D中包含有20%的正例和80%的负例。
I n f o ( D ) = − 0.2 ∗ log 2 0.2 − 0.8 ∗ log 2 0.8 = 0.722 Info(D) = -0.2 * \log_20.2 - 0.8 * \log_20.8 = 0.722 Info(D)=−0.2∗log20.2−0.8∗log20.8=0.722
（3）D中包含有100%的正例和0%的负例。
I n f o ( D ) = − 1 ∗ log 2 1 − 0 ∗ log 2 0 = 0 Info(D) = -1 * \log_21 - 0 * \log_20 =0 Info(D)=−1∗log21−0∗log20=0
当数据变得越来越“纯”时，熵的值变得越来越小：当D中正反例比例相同时，熵取最大值；当D中所有数据属于一个类时，熵取最小值。因此，熵可以作为数据纯净度的衡量指标。
信息增益
信息增益可以衡量划分数据集前后数据纯度提升程度。信息增益=原数据信息熵−数据划分之后的信息熵
其中，离散属性有个可能的取值{1,2,…,}，其中第个分支节点包含了中所有在属性上取值为 ^ ak的样本，记为 ^ Dk。
二、决策树简介
决策树（Decision Tree）是一种基于树结构的分类预测方法
决策树引入
决策树（Decision Tree）又称为判定树，是用于分类的一种树结构。其中每个内部结点（internal node）代表对某个属性的一次测试，叶结点（leaf）代表某个类（class）或者类的分布（class distribution），最上面的结点是根结点
决策树提供了一种展示在什么条件下会得到什么类别的方法。
决策树组成
决策树的基本组成部分：根节点、决策结点、分枝和叶子结点。树是由节点和分枝组成的层次数据结构。
决策树是描述分类过程的一种数据结构，从上端的根节点开始，各种分类原则被引用进来，并依这些分类原则将根节点的数据集划分为子集，这一划分过程直到某种约束条件满足而结束。
决策树基本原理
首先对数据进行处理，利用归纳法生成可读的规则和决策树，然后使用决策对新数据进行分析。
本质上决策树是通过一系列规则对数据进行分类的过程。
决策树技术发现数据模式和规则的核心是采用递归分割的贪婪算法。
使用 createBranch() 方法，如下所示:
def createBranch():
检测数据集中的所有数据的分类标签是否相同:
If so return 类标签
Else:
寻找划分数据集的最好特征（划分之后信息熵最小，也就是信息增益最大的特征）
划分数据集
创建分支节点
for 每个划分的子集
调用函数 createBranch （创建分支的函数）并增加返回结果到分支节点中
return 分支节点
决策树基本流程
1️⃣收集待分类的数据，这些数据的所有属性应该是完全标注的。
2️⃣设计分类原则，即数据的哪些属性可以被用来分类，以及如何将该属性量化。
3️⃣分类原则的选择，即在众多分类准则中，每一步选择哪一准则使最终的树更令人满意。
4️⃣设计分类停止条件，实际应用中数据的属性很多，真正有分类意义的属性往往是有限几个，因此在必要的时候应该停止数据集分裂：
该节点包含的数据太少不足以分裂，
继续分裂数据集对树生成的目标(例如ID3中的熵下降准则)没有贡献，
树的深度过大不宜再分。
决策树开发流程
- 收集数据: 可以使用任何方法。
- 准备数据: 树构造算法 (下面案例使用的是ID3算法，只适用于标称型数据，这就是为什么数值型数据必须离散化。 还有其他的树构造算法，比如CART) ，详情参考置顶博客。
- 分析数据: 可以使用任何方法，构造树完成之后，我们应该检查图形是否符合预期。
- 训练算法: 构造树的数据结构。
- 测试算法: 使用训练好的树计算错误率。
- 使用算法: 此步骤可以适用于任何监督学习任务，而使用决策树可以更好地理解数据的内在含义。
决策树算法特点
优点: 计算复杂度不高，输出结果易于理解，数据有缺失也能跑，可以处理不相关特征。
缺点: 容易过拟合。 适用数据类型: 数值型和标称型。
标称型：标称型目标变量的结果只在有限目标集中取值，如真与假(标称型目标变量主要用于分类)
数值型：数值型目标变量则可以从无限的数值集合中取值，如0.100，42.001等 (数值型目标变量主要用于回归分析)
三、决策树项目案例——判断鱼类和非鱼类
ID3算法原理
ID3算法在决策树各个节点上使用信息增益准则选择特征（属性）进行数据划分，从而递归地构建决策树。
具体方法
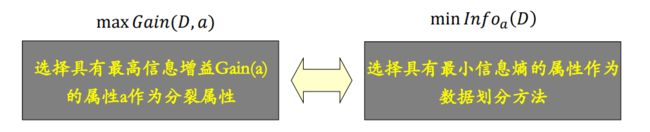
1️⃣从根节点（rootnode）开始，对节点计算所有可能的特征的信息增益，选择信息增益最大的特征作为节点的特征。
2️⃣由该特征的不同取值建立子节点。
3️⃣再对子节点递归的调用以上方法，构建决策树，直到所有特征的信息增益均很小或没有特征可以选择为止，最后得到一个决策树。
选择划分属性示例
以买电脑为例进行决策树划分说明
| 年龄 | 收入 | 学生 | 信用 | 买了电脑 |
|---|---|---|---|---|
| <30 | 高 | 否 | 一般 | 否 |
| <30 | 高 | 否 | 好 | 否 |
| 30-40 | 高 | 否 | 一般 | 是 |
| >40 | 中等 | 否 | 一般 | 是 |
| >40 | 低 | 是 | 一般 | 是 |
| >40 | 低 | 是 | 好 | 否 |
| 30-40 | 低 | 是 | 好 | 是 |
| <30 | 中 | 否 | 一般 | 否 |
| <30 | 低 | 是 | 一般 | 是 |
| >40 | 中 | 是 | 一般 | 是 |
| <30 | 中 | 是 | 好 | 是 |
| 30-40 | 中 | 否 | 好 | 是 |
| 30-40 | 高 | 是 | 一般 | 是 |
| >40 | 中 | 否 | 好 | 否 |
1️⃣ 确立初始的信息熵
|D|=14，|D1|=5，|D2|=9，即不买的有5个人，买的有9个人
信息熵如下：
I n f o ( D ) = − 5 14 log 2 5 14 − 9 14 log 2 9 14 = 0.940 Info(D)=-\frac{5}{14}\log_2\frac{5}{14}-\frac{9}{14}\log_2\frac{9}{14}=0.940 Info(D)=−145log2145−149log2149=0.940
2️⃣ 确立第一次分裂的属性
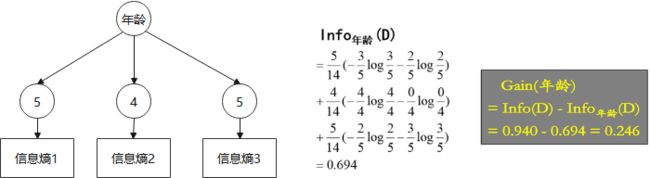
如果按照年龄划分
年龄<30的有5个,其中3个为“否”
年龄30-40的有4个,其中0个为“否”
年龄>40的有5个,其中2个为“否”
如果按照收入划分
收入=高的有4个,其中2个为“否”
收入=中的有6个,其中2个为“否”
收入=低的有4个,其中1个为“否”
如果按照学生划分
是学生的有7个,其中1个为“否”
不是学生的有7个,其中4个为“否”
如果按照信用划分
信用好的有6个,其中3个为“否”
信用一般的有8个,其中2个为“否”
综上，“年龄”属性具有最高信息增益，成为分裂属性
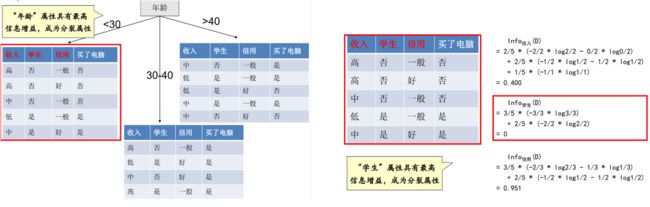
3️⃣ 确立第二次分裂的属性
按照上述方法，可以确定第二次分裂的属性为学生
4️⃣ 划分到不可划分为止
ID3算法总结
算法流程
自上而下贪婪搜索
遍历所有的属性，按照信息增益最大的属性进行分裂
根据分裂属性划分样本
重复上述流程，直至满足条件结束
优点
分类过程和领域知识无关，几乎所有模式和场景都可以得到结果
缺点
ID3算法倾向于选择属性值较多的属性，有些时候不能提供有价值的信息
不适用于连续变量
只能用于分类
一次只用一个特征值进行划分
在样本量较小时，可能会导致过度分类
对属性值缺失的情况无法处理
项目概述
根据以下 2 个特征，将动物分成两类: 鱼类和非鱼类。
特征:
- 不浮出水面是否可以生存
- 是否有脚蹼
开发流程
收集数据
| 不浮出水面是否可以生存? | 是否有脚蹼? | 是吗？ |
|---|---|---|
| Yes | Yes | Yes |
| Yes | Yes | Yes |
| Yes | No | No |
| No | Yes | No |
| No | Yes | No |
使用createDataSet()函数输入数据
def createDataSet():
dataSet = [[1, 1, '是'], [1, 1, '是'], [1, 0, '不是'], [0, 1, '不是'],
[0, 1, '不是']]
labels = ['不浮出水面是否可以生存', '是否有脚蹼']
return dataSet, labels
准备数据
此处，由于我们输入的数据本身就是离散化数据，所以这一步就省略了。
分析数据
使用如下公式计算计算给定数据集的信息熵：
I n f o ( D ) = − ∑ i = 1 m p i log 2 p i Info(D)=-\sum^m_{i=1}p_i\log_2p_i Info(D)=−i=1∑mpilog2pi
def calInfoEntropy(dataSet):
"""计算信息熵
Args:
dataSet 数据集
Returns:
返回 每一组feature下的某个分类下的信息熵
"""
# 统计标签出现的次数
label_count = Counter(data[-1] for data in dataSet)
# 计算概率
probs = [p[1] / len(dataSet) for p in label_count.items()]
# 计算香农熵
infoEntropy = sum([-p * log(p, 2) for p in probs])
return infoEntropy
按照给定特征划分数据集
def splitDataSet(dataSet, index, value):
"""就是依据index列进行分类，如果index列的数据等于 value的时候，就要将 index 划分到我们创建的新的数据集中
Args:
dataSet 数据集 待划分的数据集
index 表示每一行的index列 划分数据集的特征
value 表示index列对应的value值 需要返回的特征的值。
Returns:
index列为value的数据集【该数据集需要排除index列】
"""
retDataSet = []
for featVec in dataSet:
# index列为value的数据集【该数据集需要排除index列】
# 判断index列的值是否为value
if featVec[index] == value:
reducedFeatVec = featVec[:index]
reducedFeatVec.extend(featVec[index+1:])
# 收集结果值 index列为value的行【该行需要排除index列】
retDataSet.append(reducedFeatVec)
return retDataSet
选择最好的数据集划分方式：具有最高信息增益
def chooseBestFeatureToSplit(dataSet):
"""chooseBestFeatureToSplit(选择最好的特征)
Args:
dataSet 数据集
Returns:
bestFeature 最优的特征列
"""
# 求特征数
numFeatures = len(dataSet[0]) - 1
# 数据集的原始信息熵
baseEntropy = calInfoEntropy(dataSet)
# 最优的信息增益值, 和最优的Featurn编号
bestInfoGain, bestFeature = 0.0, -1
# 遍历所有的特征
for i in range(numFeatures):
# 获取对应的feature下的所有数据
featList = [example[i] for example in dataSet]
# 获取剔重后的集合，使用set对list数据进行去重
uniqueVals = set(featList)
# 创建一个临时的信息熵
newEntropy = 0.0
# 遍历某一列的value集合，计算该列的信息熵
# 遍历当前特征中的所有唯一属性值，对每个唯一属性值划分一次数据集
# 计算数据集的新熵值，并对所有唯一特征值得到的熵求和。
for value in uniqueVals:
subDataSet = splitDataSet(dataSet, i, value)
# 计算概率
prob = len(subDataSet)/float(len(dataSet))
# 计算信息熵
newEntropy += prob * calInfoEntropy(subDataSet)。
infoGain = baseEntropy - newEntropy
print('infoGain=', infoGain, 'bestFeature=', i, baseEntropy, newEntropy)
if (infoGain > bestInfoGain):
bestInfoGain = infoGain
bestFeature = i
return bestFeature
训练算法
创建树的函数代码如下:
def majorityCnt(classList):
"""majorityCnt(选择出现次数最多的一个结果)
Args:
classList label列的集合
Returns:
bestFeature 最优的特征列
"""
major_label = Counter(classList).most_common(1)[0]
return major_label
def createTree(dataSet, labels):
classList = [example[-1] for example in dataSet]
# 如果数据集的最后一列的第一个值出现的次数=整个集合的数量，也就说只有一个类别，就只直接返回结果就行
# 第一个停止条件: 所有的类标签完全相同，则直接返回该类标签。
# count() 函数是统计括号中的值在list中出现的次数
if classList.count(classList[0]) == len(classList):
return classList[0]
# 如果数据集只有1列，那么最初出现label次数最多的一类，作为结果
# 第二个停止条件: 使用完了所有特征，仍然不能将数据集划分成仅包含唯一类别的分组。
if len(dataSet[0]) == 1:
return majorityCnt(classList)
# 选择最优的列，得到最优列对应的label含义
bestFeat = chooseBestFeatureToSplit(dataSet)
# 获取label的名称
bestFeatLabel = labels[bestFeat]
# 初始化myTree
myTree = {bestFeatLabel: {}}
# 注: labels列表是可变对象，在PYTHON函数中作为参数时传址引用，能够被全局修改
# 所以这行代码导致函数外的同名变量被删除了元素，造成例句无法执行，提示'no surfacing' is not in list
del(labels[bestFeat])
# 取出最优列，然后它的branch做分类
featValues = [example[bestFeat] for example in dataSet]
uniqueVals = set(featValues)
for value in uniqueVals:
# 求出剩余的标签label
subLabels = labels[:]
# 遍历当前选择特征包含的所有属性值，在每个数据集划分上递归调用函数createTree()
myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), subLabels)
# print ('myTree', value, myTree)
return myTree
算法得出的决策树如下：
测试算法
def classify(inputTree, featLabels, testVec):
"""classify(给输入的节点，进行分类)
Args:
inputTree 决策树模型
featLabels Feature标签对应的名称
testVec 测试输入的数据
Returns:
classLabel 分类的结果值，需要映射label才能知道名称
"""
# 获取tree的根节点对于的key值
firstStr = list(inputTree.keys())[0]
# 通过key得到根节点对应的value
secondDict = inputTree[firstStr]
# 判断根节点名称获取根节点在label中的先后顺序，这样就知道输入的testVec怎么开始对照树来做分类
featIndex = featLabels.index(firstStr)
# 测试数据，找到根节点对应的label位置，也就知道从输入的数据的第几位来开始分类
key = testVec[featIndex]
valueOfFeat = secondDict[key]
print('+++', firstStr, 'xxx', secondDict, '---', key, '>>>', valueOfFeat)
# 判断分枝是否结束: 判断valueOfFeat是否是dict类型
if isinstance(valueOfFeat, dict):
classLabel = classify(valueOfFeat, featLabels, testVec)
else:
classLabel = valueOfFeat
return classLabel
def fishTest():
# 1.创建数据和结果标签
myDat, labels = createDataSet()
myTree = createTree(myDat, copy.deepcopy(labels))
# [1, 1]表示要取的分支上的节点位置，对应的结果值
print(classify(myTree, labels, [1, 1]))
+++ 不浮出水面是否可以生存 xxx {0: '不是', 1: {'是否有脚蹼': {0: '不是', 1: '是'}}} --- 1 >>> {'是否有脚蹼': {0: '不是', 1: '是'}}
+++ 是否有脚蹼 xxx {0: '不是', 1: '是'} --- 1 >>> 是
是
使用算法:
此步骤可以适用于任何监督学习任务，而使用决策树可以更好地理解数据的内在含义。