OpenGL第五讲——模型视图变换和投影变换
Chapter5 OpenGL变换
几种不同的变换:
- 视图变换:从不同的位置去观察它
- 模型变换:移动、旋转、放大、缩放
- 近大远小的透视效果、投影变换
5.1 模型变换和视图变换
从“相对移动”的观点来看,改变观察点的位置与方向和改变物体本身的位置与方向具有等效性。在OpenGL中,实现这两种功能甚至使用的是同样的函数。
由于模型和视图的变换都通过矩阵运算来实现,在进行变换前,应先设置当前操作的矩阵为“模型视图矩阵”。设置的方法是以GL_MODELVIEW为参数调用glMatrixMode函数:
glMatrixMode(GL_MODELVIEW);
通常,我们需要在进行变换前把当前矩阵设置为单位矩阵。这也只需要一行代码:
glLoadIdentity();
模型和视图变换主要涉及3个函数(对应移动、旋转和缩放):
-
glTranslate*,把当前矩阵和一个表示移动物体的矩阵相乘。三个参数分别表示了在三个坐标上的位移值。
void glTranslatef (GLfloat x, GLfloat y, GLfloat z); -
glRotate*,把当前矩阵和一个表示旋转物体的矩阵相乘。物体将绕着(0,0,0)到(x,y,z)的直线以逆时针旋转,参数angle表示旋转的角度。
void glRotatef(GLfloat angle,GLfloat x,GLfloat y,GLfloat z)使用右手定则,从大拇指的方向为(0,0,0)到(x,y,z)的方向,然后四指的方向为旋转的方向。
-
glScale*,把当前矩阵和一个表示缩放物体的矩阵相乘。x,y,z分别表示在该方向上的缩放比例。
void glScalef (GLfloat x, GLfloat y, GLfloat z)
需要特别注意的点如下!!!总的来说就是实际的变换的顺序和代码中写的顺序是相反的,原因是矩阵相乘的结合律
假设当前矩阵为单位矩阵,然后先乘以一个表示旋转的矩阵R,再乘以一个表示移动的矩阵T,最后得到的矩阵再乘上每一个顶点的坐标矩阵v。所以,经过变换得到的顶点坐标就是((RT)v)。由于矩阵乘法的结合率,((RT)v) = (R(Tv)),换句话说,实际上是先进行移动,然后进行旋转。即:实际变换的顺序与代码中写的顺序是相反的。由于“先移动后旋转”和“先旋转后移动”得到的结果很可能不同,初学的时候需要特别注意这一点。
或者,不如换一种思路?
让我们想象,坐标并不是固定不变的。旋转的时候,坐标系统随着物体旋转。移动的时候,坐标系统随着物体移动。如此一来,就不需要考虑代码的顺序反转的问题了。
以上都是针对改变物体的位置和方向来介绍的。如果要改变观察点的位置,除了配合使用glRotate和glTranslate函数以外,还可以使用这个函数:gluLookAt。它的参数比较多,前三个参数表示了观察点的位置,中间三个参数表示了观察目标的位置,最后三个参数代表从(0,0,0)到(x,y,z)的直线,它表示了观察者认为的“上”方向。
void gluLookAt(GLdouble eyex,GLdouble eyey,GLdouble eyez,GLdouble centerx,GLdouble centery,GLdouble centerz,GLdouble upx,GLdouble upy,GLdouble upz);
该函数定义一个视图矩阵,并与当前矩阵相乘。
第一组eyex, eyey,eyez相机在世界坐标的位置
第二组centerx,centery,centerz相机镜头对准的物体在世界坐标的位置
第三组upx,upy,upz相机向上的方向在世界坐标中的方向
你把相机想象成为你自己的脑袋:
第一组数据就是脑袋的位置
第二组数据就是眼睛看的物体的位置
第三组就是头顶朝向的方向(因为你可以歪着头看同一个物体)。
原文链接:https://blog.csdn.net/qq_34911636/article/details/86686906
5. 2 投影变换
投影变换就是定义一个可视空间,可视空间以外的物体不会被绘制到屏幕上。(注意,从现在起,坐标可以不再是-1.0到1.0了!)
OpenGL支持两种类型的投影变换:
- 透视投影
- 正投影
投影也是使用矩阵来实现的。如果需要操作投影矩阵,需要以GL_PROJECTION为参数调用glMatrixMode函数。
glMatrixMode(GL_PROJECTION);
通常,我们需要在进行变换前把当前矩阵设置为单位矩阵。(和之前一样)
glLoadIdentity();
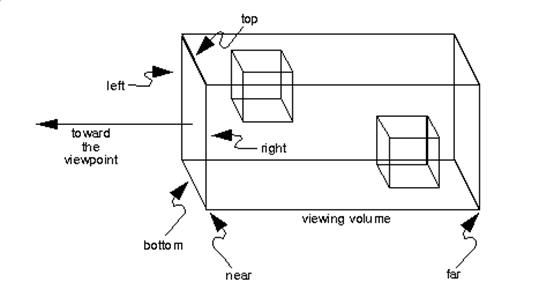
使用glFrustum函数可以将当前的可视空间设置为透视投影空间。其参数的意义如下图
也可以使用更常用的gluPerspective函数。
如果说
gluLookAt定义了相机的位置,那么gluPerspective定义了相机的视野范围,比近裁面(near)近的不会被展示在视野里,同理,比远裁面(far)远的也不会。
void gluPerspective (GLdouble fovy, GLdouble aspect, GLdouble near, GLdouble far)
其参数的意义如下图:
正投影相当于在无限远处观察得到的结果,它只是一种理想状态。但对于计算机来说,使用正投影有可能获得更好的运行速度。
使用glOrtho函数可以将当前的可视空间设置为正投影空间。其参数的意义如下图:
如果绘制的图形空间本身就是二维的,可以使用
gluOrtho2D。他的使用类似于glOrgho。
5.3 视口变换
当一切工作已经就绪,只需要把像素绘制到屏幕上了。这时候还剩最后一个问题:应该把像素绘制到窗口的哪个区域呢?通常情况下,默认是完整的填充整个窗口,但我们完全可以只填充一半。
使用glViewport来定义视口。其中前两个参数定义了视口的左下脚(0,0表示最左下方),后两个参数分别是宽度和高度。
5.4 操作矩阵堆栈
我们在进行矩阵操作时,有可能需要先保存某个矩阵,过一段时间再恢复它。当我们需要保存时,调用glPushMatrix函数,它相当于把矩阵(相当于盘子)放到堆栈上。当需要恢复最近一次的保存时,调用glPopMatrix函数,它相当于把矩阵从堆栈上取下。
OpenGL规定堆栈的容量至少可以容纳32个矩阵,某些OpenGL实现中,堆栈的容量实际上超过了32个。因此不必过于担心矩阵的容量问题。
通常,用这种先保存后恢复的措施,比先变换再逆变换要更方便,更快速。
注意:模型视图矩阵和投影矩阵都有相应的堆栈。使用
glMatrixMode来指定当前操作的究竟是模型视图矩阵还是投影矩阵。
5.5 综合举例
#include