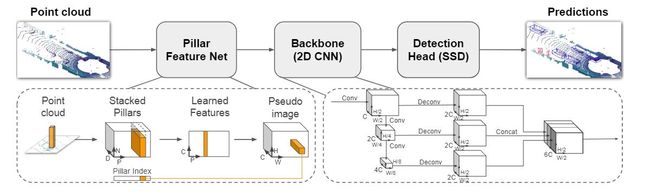
【3D目标检测】PointPillars: Fast Encoders for Object Detection from Point Clouds

概述

首先，本文是基于点云，但不是将点云处理成体素，而是体柱！
提出动机与贡献： 比较主流的一种方式就是将点云编码成体素，但是这就使得后面需要使用3D卷积进行特征提取，开销比较大（哪怕SECOND中引入了稀疏卷积，计算量还是比2D卷积大）；另外一种思路就是从俯视角度将点云数据进行处理，得到伪图片的数据，之后使用2D卷积处理，开销小了，但是得到伪图片的过程中，丢失了很多信息。因此作者在一定程度上融合了这两种方法的思想，提出了一种新的点云编码方式，在这种方式下，仅仅使用2D卷积就可以实现端到端的3D目标检测。

这种编码方式的优点：

1. 通过学习特征而不是依赖固定编码器，PointPillars 可以利用点云表示的全部信息。(什么意思？)
2. 体柱是主要考虑的是x、y的，z方向的划分不用考虑（相对于体素而言方便了，并且体柱也比体素少了很多）
3. 所有的操作都是用2D卷积而没有使用3D卷积，计算效率大大增强

注:
转成鸟瞰图的优点：没有尺度模糊性（啥意思？？），没有遮挡
转成鸟瞰图的缺点：会导致鸟瞰图很稀疏，而标准卷积比较适合处理稠密的图像。所以一个常见的处理思路就是将平面划分为若干个网格，然后聚合网格内点的特征作为当前网格的特征。（点云稀疏，所以将点云划分为体素，两者不能说是十分相似，只能说是一模一样）

细节

网络结构

流程：

1. 一个特征编码网络，将点云划分为体柱，然后构成稀疏的伪图片数据（3维张量）
2. 在伪图片数据上使用2D卷积提取特征
3. 使用SSD作为检测头得到最终分类和检测的结果
   

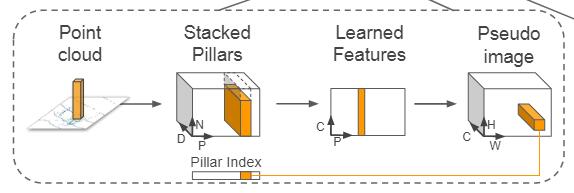
从点云得到伪图像

详细表述：
假设点云中的点$l$有$D=4$个特征$x,y,z,r$，我们将平面空间划分为若干个网格，接着将点云中的点按照$x、y$坐标分配到对应网格中，得到一系列的体柱，假设非空体柱的个数是$P$，非空体柱内的点数阈值是$N$。和体素化时候的处理一样，如果体柱内的点超过了$N$就只采样$N$个点，不足$N$就用0填充。接下来给体柱中的点添加额外的5个特征，分别是$x_c,y_c,z_c,x_p,y_p$，前三者表示的是体柱中点的几何平均值（相当于是质心），后两者表示的是当前点与质心的相对偏移，这样的话，每个点的特征D就从4变为了9。
我们知道体素是稀疏的，虽然体柱在体素的基础上放宽了一定的限制，但体柱也还是稀疏的（作者的配置下，KITTI上的稀疏性大概是97%）。通过超参数的调整，我们可以使得张量$(D,P,N)$相对稠密（这个张量表示当前有P个非空体素，每个体素内有N个点，每个点有D个对应的特征）。接着使用一个简单版本的PointNet的结构，进行点级的特征提取得到一个$(C,P,N)$，然后通过一个max pool操作得到体柱的特征$(C,P)$（P个体素，每个体素用C个特征表示），接着将它映射到原始的体柱空间，得到稀疏的伪图片数据$(C,H,W)$，其中H、W就是原始体柱空间的宽和高。

概述：数据流变化：输入点云数据$(points-num,4)$，将平面划分成$H\ast W$个网格，每个网格就是一个体柱，将点云中的点放到对应的体柱中，取出其中非空的体柱构成张量$(9,P,N)$，接下来通过类似pointNet的结构得到一个高纬的表示$(C,P,N)$，然后是一个max pool操作得到非空体柱的特征$(C,P)$，接着将它映射回原体柱空间中得到最终的稀疏张量$(C,H,W)$

对比VoxelNet：数据流变化：输入点云数据$(points-num,4)$，将空间划分成$D\ast H\ast W$个体素，将点云中的点放到对应的体素中，取出其中非空的体素构成张量$(7,P,N)$，接下来通过类似pointNet的结构（VFE）得到一个高纬的表示$(C,P,N)$，然后是一个max pool操作得到非空体素的特征$(C,P)$，接着将它映射回原体素空间中得到最终的稀疏张量$(C,D,H,W)$

对比的一个感受：在获得点云的特征表示的过程中，两者的流程以及中间的过程是一样的，区别主要就在于编码点云的方式，是采用体素的形式编码还是采用体柱的方式编码。

骨干网络

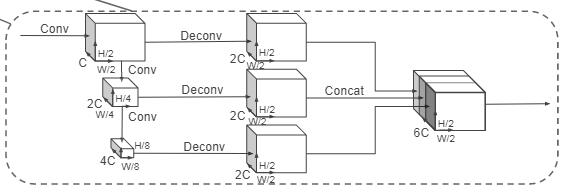
刚才我们说了，基于体柱的点云特征表示是一个伪图像的数据，对于这种3维的张量我们就可以使用2D卷积处理，这里处理的过程类似于VoxelNet的2D特征提取网络。

对比VoxelNet：VoxelNet采用3D卷积+2D卷积做特征提取，而PointPillars只使用2D卷积

检测头

使用SSD作检测头

损失函数

本文的损失函数与SECOND中使用的损失函数是一模一样的。