机器学习吴恩达编程作业题5—正则化线性回归和偏差/方差
1、正则化线性回归
1.1可视化数据集
我们将从可视化数据集开始,其中包含水位变化的历史记录x和流出水坝的水量y。将实现线性回归,并使用它来拟合数据的直线并绘制学习曲线。将实现多项式回归,以找到更好的数据拟合。复制ex5data1数据集到D:\Machine Learning\ex5目录下。直接调用plot函数进行数据集的绘制。
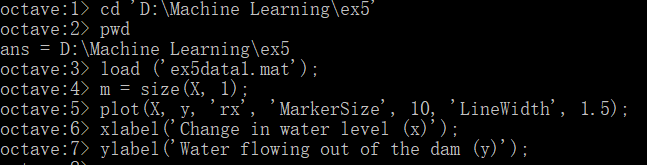
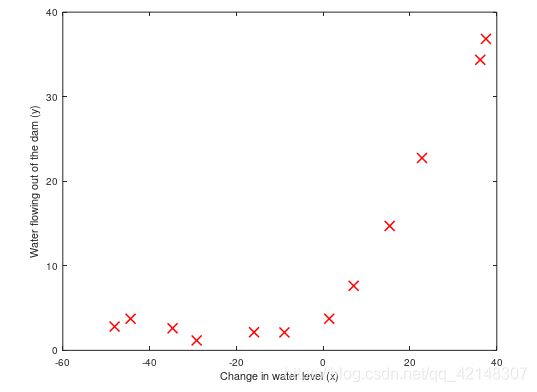
1.2正则化线性回归成本函数和梯度

在当前目录下建立linearRegCostFunction.m文件:
function [J, grad] = linearRegCostFunction(X, y, theta, lambda)
m = length(y);
J = 0;
grad = zeros(size(theta));
J = (sum((X * theta - y) .^ 2) + lambda * sum(theta(2:end) .^ 2))/2/m;
%不正则化θ0
grad = sum((X * theta - y) .* X, 1)' / m;
%先转置成1*12,再对每一列求和
grad(2:end) = grad(2:end) + theta(2:end) * lambda / m;
grad = grad(:);
end1.3拟合线性回归
- 首先优化θ参数,在当前目录下建立fmincg.m文件,代码实现参照前面章节。在当前目录下建立trainLinearReg.m文件,调用fmincg函数,得到优化的参数
function [theta] = trainLinearReg(X, y, lambda)
initial_theta = zeros(size(X, 2), 1);
costFunction = @(t) linearRegCostFunction(X, y, t, lambda);
options = optimset('MaxIter', 200, 'GradObj', 'on');
%迭代次数为200次
theta = fmincg(costFunction, initial_theta, options);
end2、偏差方差
2.1学习曲线
绘制学习曲线,在学习曲线上绘制训练和测试错误,以诊断偏差方差问题。训练误差不包括正则化项。计算训练误差的一种方法是使用现有的代价函数,仅当使用它来计算训练误差和交叉验证误差时,才将λ设置为0。
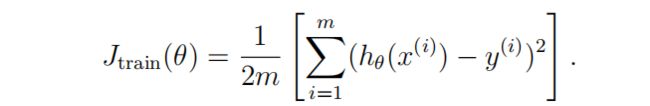
计算训练集误差时,请确保在训练子集(即X(1:n,:)和y(1:n))上计算它(而不是整个训练集)。但是,对于交叉验证错误,您应该在整个交叉验证集上计算它。您应该将计算出的错误存储在向量error train和error val中。
在当前目录下建立learningCurve.m文件,完成学习曲线的绘制工作:
function [error_train, error_val] = ...
learningCurve(X, y, Xval, yval, lambda)
%返回值是误差向量,也就是每增加一个个例计算后的误差组成的
m = size(X, 1);
error_train = zeros(m, 1);
error_val = zeros(m, 1);
m_cv = size(Xval, 1);
%交叉验证集个例数目
size(X)
for i = 1:m,
theta = trainLinearReg(X(1:i, :), y(1:i), lambda);
%训练出相应的θ矩阵
error_train(i) = sum((X(1:i, :) * theta - y(1:i)) .^ 2) / 2 / i;
%训练集的误差向量
error_val(i) = sum((Xval * theta - yval) .^ 2) / 2 / m_cv;
%交叉验证集的误差向量
end;
end


可以观察到当训练示例的数量增加时,训练错误和交叉验证错误都很高。这反映了模型中的一个高偏差问题——线性回归模型过于简单,无法很好地拟合我们的数据集。将实现多项式回归以适合此数据集的更好的模型。
3、多项式回归
我们的线性模型的问题是,它对数据过于简单,导致了欠拟合(高偏差)。
在当前目录下建立polyFeatures.m文件,以便函数将大小为m×1的原始训练集X映射为其更高的幂。具体地说,当一个m×1大小的训练集X传递给函数时,函数应该返回一个m×pX矩阵,其中第1列保存X的原始值,第2列保存X.^2 的值,第3列保存X.^3的值,依此类推。
function [X_poly] = polyFeatures(X, p)
%X_poly是m*p,p是最高的次幂
X_poly = zeros(numel(X), p);
for i = 1:p,
X_poly(:, i) = X .^ i;
end;
end使用8次多项式。结果表明,如果我们直接在投影数据上运行训练,将不能很好地工作,因为特征将被严重地缩放(例如,一个x=40的例子现在将有一个特征x8=408=6.5×1012)。因此,您需要使用特性规范化。![]() 在当前目录下建立featureNormalize.m文件:
在当前目录下建立featureNormalize.m文件:
function [X_norm, mu, sigma] = featureNormalize(X)
mu = mean(X);
%均值
X_norm = bsxfun(@minus, X, mu);
%这个函数第一个参数是减法,该函数就是第二个参数减第三个数
sigma = std(X_norm);
%标准差
X_norm = bsxfun(@rdivide, X_norm, sigma);
%这个函数第一个参数是除法,该函数就是第二个参数除第三个数
end![]()
在λ=0时,利用特征规范化后的高次多项式来获得训练后的参数θ。
然后再画出规范化后的高次多项式拟合的曲线,这里利用plotFit函数完成,在当前目录下建立plotFit.m文件:
function plotFit(min_x, max_x, mu, sigma, theta, p)
hold on;
x = (min_x - 15: 0.05 : max_x + 25)';
%设置x的范围,步长0.05
X_poly = polyFeatures(x, p);
X_poly = bsxfun(@minus, X_poly, mu);
X_poly = bsxfun(@rdivide, X_poly, sigma);
%特征规范化的X矩阵
X_poly = [ones(size(x, 1), 1) X_poly];
plot(x, X_poly * theta, '--', 'LineWidth', 2)
hold off
end在Octave中画出拟合的曲线以及训练误差和交叉验证误差曲线



多项式拟合能够很好地跟踪数据点,从而获得较低的训练误差。
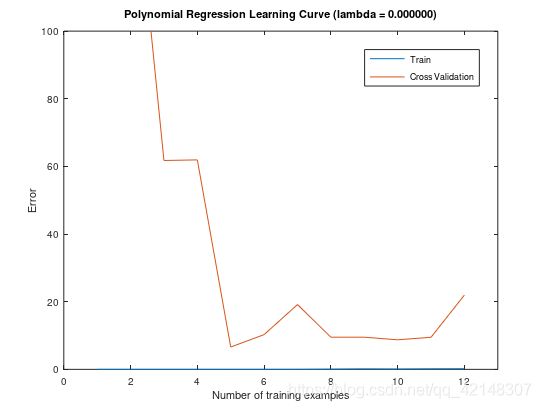
低训练误差低,但交叉验证误差高。训练错误和交叉验证错误之间存在差距,表明存在高方差问题。解决过拟合(高方差)问题的一种方法是在模型中添加正则化。将尝试不同的λ参数,以了解正则化如何导致更好的模型。
3.1使用交叉验证集进行选择λ
您注意到λ的值可以显著影响训练集和交叉验证集上正则化多项式回归的结果。特别是,没有正则化的模型(λ=0)很好地拟合了训练集,但不能推广。反之,正则化太多(λ=100)的模型不能很好地拟合训练集和测试集。选择一个好的λ(例如,λ=1)可以很好地拟合数据。
在本节中,您将实现一个自动选择λ参数的方法。具体地说,您将使用交叉验证集来评估。
计算不同的λ值,计算训练误差和交叉验证误差。您应该在以下范围内尝试λ:{0,0.001,0.003,0.01,0.03,0.1,0.3,1,3,10}。
在当前目录下建立validationCurve.m文件:
function [lambda_vec, error_train, error_val] = ...
validationCurve(X, y, Xval, yval)
%第三个、第四个参数是交叉验证集数据
%返回值是λ矩阵、训练集和交叉验证集误差
lambda_vec = [0 0.001 0.003 0.01 0.03 0.1 0.3 1 3 10]';
%设置λ矩阵
error_train = zeros(length(lambda_vec), 1);
error_val = zeros(length(lambda_vec), 1);
num = length(lambda_vec);
%循环次数
for i = 1:num,
theta = trainLinearReg(X, y, lambda_vec(i));
[J, grad] = linearRegCostFunction(X, y, theta, 0);
error_train(i) = J;
[J, grad] = linearRegCostFunction(Xval, yval, theta, 0);
error_val(i) = J;
end;
end