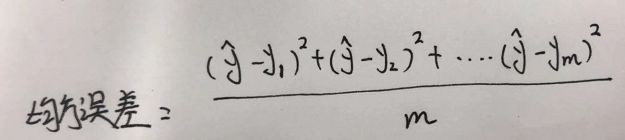学习机器学习四 回归模型——线性回归、L1正则化(Lasso回归)、L2正则化(ridge回归)

还记得什么是回归吗？回忆下回归就是连续的输出，分类是离散的。

回归模型一般分为：①线性回归——就是线性方程，类似为一元一次方程（y=wx+b），比如你的年龄；

                                ②逻辑回归（类似为曲线方程）

线性回归

先来详细的学习下线性回归，线性回归就是回归模型中最简单的，就像一元一次方程（y=wx+b）是数学方程组中最简单易学的一样。假设我们要知道y的取值范围，我们只需要知道w和b的值就可以了。

打个比方来说，我们来预测下某房子的价格，在这个问题中我们正常会需要两个特征，一个是房子地段信息，一个是房子面积。不难理解吧，这时候我们可以构建一个数学方程ŷ =x1+x2+b（b是常数，可要可不要）。

其中x1代表地段，这个地段的值肯定是某一个变量（也称权重系数）w和基础数值f组成的，比如地段平均是3000，好的地段和不好的地段之间肯定存在某一个变量w来决定价值，才能决定地段的高低之分，即x1=w₁f₁。所以我们的方程又可以变成——   ŷ =w₁f₁+x2+b，能理解吗？

接着分解x2代表的面积b，我们详细分解下，如果有建筑面积和套内面积等，我们也可以找到一个方程组打个比方x₂f₂来表示只针对面积的对吧，那么问题解就变成了ŷ =w₁f₁+w₂f₂+b。

我们接着可以看出来，我们关键点就在w₁和w₂上，也就是说线性回归的目标就是学习这两个权重系数：w₁和w₂。

注意下：有多少特征就有多少X，仅有一个特征变量的特殊例子，我们叫做简单线性回归。有M个特征的，就可以分解出M个权重系数，用公式表达为：

我们再稍深入的理解下这个线性方程模型，如果只有一个特征，那么ŷ 的取值就是一条线对吧（ŷ =w₁f₁+b）。有两个特征，那么ŷ 取值就构成在一个平面对吧。那么有N维（就是需要有N个特征）时，这就会变成多个著名的超平面。如果空间是N维的，那么它的超平面就是N-1维。（不难理解，2个特征构成1个平面，N个特征就构成N-1个平面）

接着来解释下为什么不是y而是ŷ ，通常我们会将真实值表示为y，预测值（就是有一定偏差的值表示为ŷ ），也就是说y=ŷ +b。这个b就是常数，就是与y的差距。我们学过数学的都知道，这b就是ŷ 的截距（也就是预测值与真实值的差距），如图：

最终，线性回归的目标就是学习一组权重参数?ᵢ，进而在预测时尽可能的接近真实的值。

还记得之前说过的分类器和回归的评分指标吗？分类器可以直接得到模型的准确率，回归里面的评分函数常常使用本函数（或者损失函数）来表示。回忆一下前面笔记三的内容，我们有多个评分函数来评价一个回归模型的性能，还记得最常用的成本函数就是均方误差，它计算了每个数据点i的预测值ŷ和目标输出值yᵢ之间的误差平方（ŷ-yᵢ)²，然后取所有的误差平方的平均值。

现在我们了解了这其中的奥妙，就可以转化成一个优化问题了对吧？——就是找到让成本函数最小化的一组权重。直白说就是找到各个?，使得y与ŷ的截距越靠近。记得不是重合，是越靠近。这常常会用迭代算法（搞编程的都应该懂迭代）完成，就是不断去试验各个w，然后选最合适的那个。

目前学习到的简单理论应该都懂了，我们来玩一下最愉快的编码游戏吧。

我们来玩一下预测美国波士顿的房价吧，自由美利坚，枪击每一天，所以预测他的房价要抽取特征显然更为之复杂。scikit-learn为我们提供了关于波士顿房价的一个数据集：

import numpy as np
import cv2

from sklearn import datasets
from sklearn import metrics
from sklearn import model_selection
from sklearn import linear_model

%matplotlib inline
import matplotlib.pyplot as plt
plt.style.use('ggplot')
plt.rcParams.update({'font.size': 16})

# 载入关于波士顿房价的数据集
boston = datasets.load_boston()

# boston对象的结构和iris对象的结构一样，我们可以在'DESCR'中获取更多关于数据集的信息；在'data'中找到所有的数据；在'feature_names'中找到所有特征的名字，以及在'target'中找到所有的目标值。
dir(boston)  #输出['DESCR', 'data', 'feature_names', 'target']

# 通过上一步的注释，我们现在来看看是不是这样的
boston.data.shape  #输出(506, 13)，这数据集包含了506个数据点，每个数据点有13个维度，即13个特征

boston.target.shape  #输出(506,)，因为我们只有一个目标，就是预测房价

由于OpenCV中没有比较好的线性回归的实现，我们就用scikit-learn的API实现吧。

训练模型：

# 先定义一个线性回归对象
linreg = linear_model.LinearRegression()

# 我们把数据集分为训练集和测试集，你也可以多分一个验证集，但一般测试集数据量要占10%-30%这里，我们用test_size分出10%做测试集好了
X_train, X_test, y_train, y_test = model_selection.train_test_split(
    boston.data, boston.target, test_size=0.1, random_state=42
)

还记得笔记一我们讲过的OpenCV和scikit-learn的一些不同吗，OpenCV的train函数在scikit-learn中叫做fit：

# 训练模型
linreg.fit(X_train, y_train) #输出LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)

#计算均方误差，通过真实的房价y_train和我们的预测结果linreg.predict(X_train)的差值，可以得到预测的均方误差
metrics.mean_squared_error(y_train, linreg.predict(X_train))  #输出22.739484154236614

#linreg对象的score方法返回的是确定系数（R方值）
linreg.score(X_train, y_train)  #输出0.73749340919011974

到这里我们就训练模型完毕了，很简单吧。

接着测试模型：

# 为了测试模型的泛化性能，在测试数据上计算均方误差
y_pred = linreg.predict(X_test)

metrics.mean_squared_error(y_test, y_pred)  #输出15.010997321630107

我们是不是发现测试数据集上计算出来的均方误差比训练集的要小一些，这是很好的，因为我们更需要测试的结果。我们把它画出来更能看清楚我们模型是否优秀：

# 把结果画出来
plt.figure(figsize=(10, 6))
plt.plot(y_test, linewidth=3, label='ground truth')
plt.plot(y_pred, linewidth=3, label='predicted')
plt.legend(loc='best')
plt.xlabel('test data points')
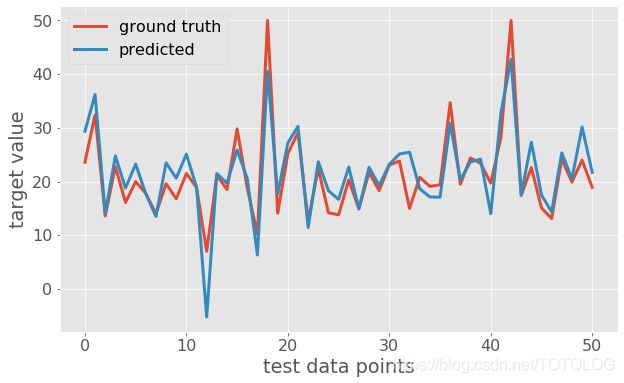
plt.ylabel('target value')  #输出

结果图：

这样看起来是不是很明显，其中蓝色的是真实的房价信息，我们预测的是房价信息是蓝色的线。一眼看上去还是很不错的模型对吧，但仔细观察就会发现，在房价的高峰或低峰时，误差还是比较大的，比如数据点12、18和42的峰点位置。

我们可以形象化数据方差的数量，这样就可以通过计算R方值来解释这个现象：

plt.figure(figsize=(10, 6))
plt.plot(y_test, y_pred, 'o')
plt.plot([-10, 60], [-10, 60], 'k--')
plt.axis([-10, 60, -10, 60])
plt.xlabel('ground truth')
plt.ylabel('predicted')

# 这将会在X坐标轴上画出真实的房价y_test，在Y坐标轴上画出我门预测的房价y_pred。我们也画出一条用于参考的对角线（使用黑色虚线k--表示），然后一个文本框显示出R²值和均方误差。
scorestr = r'R$^2$ = %.3f' % linreg.score(X_test, y_test)
errstr = 'MSE = %.3f' % metrics.mean_squared_error(y_test, y_pred)
plt.text(-5, 50, scorestr, fontsize=12)
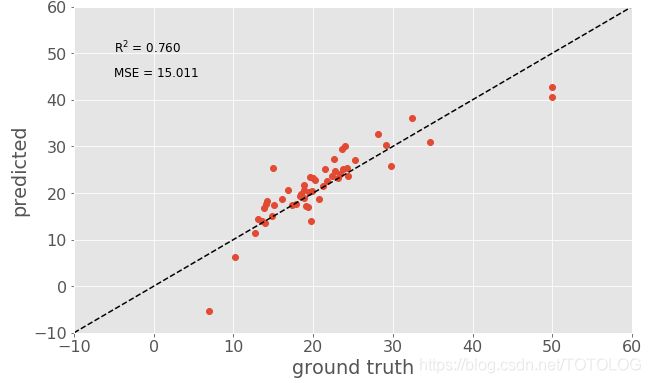
plt.text(-5, 45, errstr, fontsize=12);

生成的模型预测值与真实值的对比结果图，一个画出模型拟合度的专业方法：

如果我们的模型是完美的，那么所有数据点都将位于虚线对角线上，因为y_pred总是等于y_true。与对角线的偏差表明模型出现了一些误差，或者是数据中有一些方差是模型无法解释的。实际上，R2表明我们能够解释数据76%的离散度，平均平方误差为15.011。这些是我们可以用来比较线性回归模型和一些更复杂的模型的一些硬指标。

在指标上，我们应该已经知道分类是什么指标（准确率、精确度和召回率等），怎么求，回归是什么指标（均方误差、可释方差和决定系数），怎么求了吧。本篇如果我有什么解释错误的信息可以给我留言，欢迎大家的批评改正。

我们前面也玩了几个模型了，我们可能会发现一个问题，就是我们用训练的数据跑这个模型，会发现它基本都对了。但是我们投入到生产中，会有很多未知的数据跑这个模型，它做出的成绩却不太理想。这也就是模型它的一个泛化能力啦。在机器学习中，一些算法（比如决策树）会比其他算法更容易受影响，就算是线性回归也一样会被影响。

我们把这个模型在训练数据上很完美，实际应用起来却不太好的现象叫做——过拟合（就是泛化能力差，过分依赖特定数据）。

我们把这个模型在训练数据上表现不太好，实际应用起来更不好的现象叫做——欠拟合（就是谁用谁知道的差）。

我们主要讲下过拟合，毕竟欠拟合了你整个模型都可能推到重来吧。

降低过拟合一个常见的方法叫做“正则化”，它是通过在损失函数（我们上一篇讲到的，回归里的评分方式用损失函数表示）中添加一个独立于所有特征之外的额外限制来避免过拟合。两个最常用的正则化项如下所示：

☺L1正则化：该方法在评分函数上添加一个与所有权重（w）绝对值的和成比例的元素（例如 ŷ = ⅓ (|?₁|+| ?₂|)?₁?₁ +⅓ (|?₁|+| ?₂|)?₂?₂）。换句话说，它基于权重向量的L1范数（也叫作蛇形距离或曼哈顿距离）。也叫作Lasso回归，这就是L1正则化。

☺L2正则化：该方法在评分函数上添加一个与所有权重（w）平方和成比例的元素（例如 ŷ = ⅓ (?₁ ²+?₂ ²)?₁?₁ +⅓ (?₁ ²+?₂ ²)?₂?₂）。换句话说，它基于权重向量的L2范数（也叫作欧氏距离）。因为L2包含了一个平方操作，它对那些权重向量中比较大的离群值的惩罚力度比L1范数的惩罚力度更大。我们把这叫算法叫做“ridge回归”

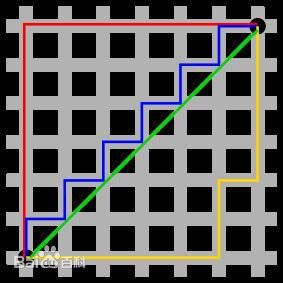
如图：

绿色的就是直线距离，也就是欧式距离，蓝色、黄色就是曼哈顿距离，也就是说曼哈顿距离就是两点间x+y的长度，你仔细看就会发现，黄色线和蓝色线是一样的长度，都等于红色线。

 

 

# 定义一个先定义一个线性回归对象
linreg = linear_model_LinearRegression()

# L1正则化
lassoreg = linear_model.Lasso()

#L2正则化
ridgereg = linear_model.RidgeeRegression()

这些学习笔记是我在拜读了Michael Beyeler著的《机器学习 使用OpenCV和Python进行智能图像处理》的自我理解，感谢。