多分类问题代码

CrossEntropyLoss — PyTorch 1.12 documentation

NLLLoss — PyTorch 1.12 documentation

代码：

import torch
from torchvision import transforms
from torchvision import datasets
from torch.utils.data import DataLoader
import torch.nn.functional as F
import torch.optim as optim
 
# prepare dataset
 
batch_size = 64
transform = transforms.Compose([transforms.ToTensor(), transforms.Normalize((0.1307,), (0.3081,))]) # 归一化,均值和方差
 
train_dataset = datasets.MNIST(root='../dataset/mnist/', train=True, download=True, transform=transform)
train_loader = DataLoader(train_dataset, shuffle=True, batch_size=batch_size)
test_dataset = datasets.MNIST(root='../dataset/mnist/', train=False, download=True, transform=transform)
test_loader = DataLoader(test_dataset, shuffle=False, batch_size=batch_size)
 
# design model using class
 
 
class Net(torch.nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        #torch.nn.Linear(784, 512)为什么是784？
        #图像是1*28*28的。
        self.l1 = torch.nn.Linear(784, 512)
        self.l2 = torch.nn.Linear(512, 256)
        self.l3 = torch.nn.Linear(256, 128)
        self.l4 = torch.nn.Linear(128, 64)
        #因为数据集的是0-9的图像，所以输出是10维的
        self.l5 = torch.nn.Linear(64, 10)
 
    def forward(self, x):
        #把向量铺平
        x = x.view(-1, 784)  
        x = F.relu(self.l1(x))
        x = F.relu(self.l2(x))
        x = F.relu(self.l3(x))
        x = F.relu(self.l4(x))
        # 最后一层不做激活，不进行非线性变换
        return self.l5(x)  
 
 
model = Net()
 
# construct loss and optimizer
criterion = torch.nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.5)
 
# training cycle forward, backward, update
#将训练封装
#batch_idx表示运行的batch 的次数。
def train(epoch):
    running_loss = 0.0
    for batch_idx, data in enumerate(train_loader, 0):
        #获得一个批次的数据和标签
        inputs, target = data
        optimizer.zero_grad()
        #获得模型预测结果(64, 10)
        outputs = model(inputs)
        
        loss = criterion(outputs, target)
        loss.backward()
        optimizer.step()
        #进行平均损失的计算
        running_loss += loss.item()
        #每跑完300个batch,做一次记录
        if batch_idx % 300 == 299:
            #epoch+1, batch_idx+1
            #epoch in range(10)表示【0，10），所以加1
            #for batch_idx, data in enumerate(train_loader, 0)的索引值从0开始所以加1
            print('[%d, %5d] loss: %.3f' % (epoch+1, batch_idx+1, running_loss/300))
            running_loss = 0.0
 
#将测试封装 
def test():
    correct = 0
    total = 0
    with torch.no_grad():
        #for i,data in enumerate(train_loader,0):
            
            #x_data,y_data=data
        for data in test_loader:
            images, labels = data
            outputs = model(images)

            #dim = 1 表示输出所在行的最大值
            #dim = 0 表示输出所在列的最大值
            _, predicted = torch.max(outputs.data, dim=1)
            
            total += labels.size(0)

            ## 张量之间的比较运算
            correct += (predicted == labels).sum().item()
    print('accuracy on test set: %d %% ' % (100*correct/total))
 
#主函数
if __name__ == '__main__':
    for epoch in range(10):
        train(epoch)
        test()

下载数据集Remote end closed connection without response

下载数据集：Remote end closed connection without response 报错，换成热点，可能是网络问题。

下载完全会显示如下信息：

Downloading http://yann.lecun.com/exdb/mnist/train-images-idx3-ubyte.gz
Downloading http://yann.lecun.com/exdb/mnist/train-images-idx3-ubyte.gz to ../dataset/mnist/MNIST\raw\train-images-idx3-ubyte.gz
100.0%
Extracting ../dataset/mnist/MNIST\raw\train-images-idx3-ubyte.gz to ../dataset/mnist/MNIST\raw

Downloading http://yann.lecun.com/exdb/mnist/train-labels-idx1-ubyte.gz
Downloading http://yann.lecun.com/exdb/mnist/train-labels-idx1-ubyte.gz to ../dataset/mnist/MNIST\raw\train-labels-idx1-ubyte.gz
100.0%
Extracting ../dataset/mnist/MNIST\raw\train-labels-idx1-ubyte.gz to ../dataset/mnist/MNIST\raw

Downloading http://yann.lecun.com/exdb/mnist/t10k-images-idx3-ubyte.gz
Downloading http://yann.lecun.com/exdb/mnist/t10k-images-idx3-ubyte.gz to ../dataset/mnist/MNIST\raw\t10k-images-idx3-ubyte.gz
100.0%
Extracting ../dataset/mnist/MNIST\raw\t10k-images-idx3-ubyte.gz to ../dataset/mnist/MNIST\raw

Downloading http://yann.lecun.com/exdb/mnist/t10k-labels-idx1-ubyte.gz
Downloading http://yann.lecun.com/exdb/mnist/t10k-labels-idx1-ubyte.gz to ../dataset/mnist/MNIST\raw\t10k-labels-idx1-ubyte.gz
100.0%
Extracting ../dataset/mnist/MNIST\raw\t10k-labels-idx1-ubyte.gz to ../dataset/mnist/MNIST\raw

要解决的问题：对minst数据集进行图像分类。

样本集x：图像（28*28） 输出y：0-9的数字。

思路：

把图像分类问题，转化成能用线性回归方法解决的分类问题。

线性回归的输入可以是值，或者矩阵，所以考虑研究图像的像素值，把图像数据转化成二维的矩阵，矩阵每个元素代表像素值。

转化成10个二分类的问题，对于每个图像，做10个输出（判断是不是0，是不是1，是不是2，做十次判断，输出10个概率值)。但是这个方法10个概率值是互不影响的，不会互相抑制，概率值的和也不一定是1，很难做出正确的判断。

为了解决这个问题,需要使用softmax,它可以使概率之和等于1，使概率值互相抑制。

z表示输出，softmax是对输出的概率值进行转化。计算公式如图所示：

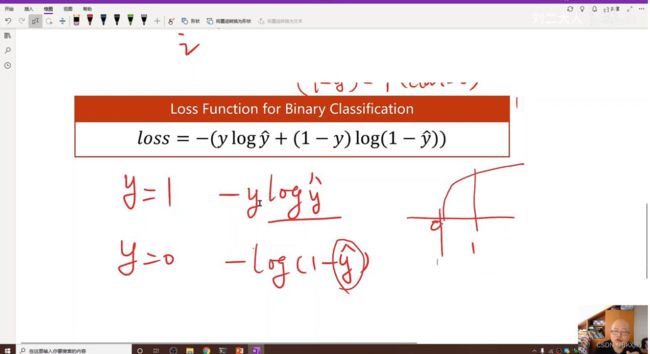
怎么计算损失？ 

将输出处理后使用nnloss计算损失。

 原本交叉熵的公式:

nnloss的公式： 

只计算了Y=1的损失。 

z的数据处理和整个计算损失的只要使用crossentropyLoss(）函数即可。

 

1.导入数据集：

import torch.nn.functional as F 是为了使用F.relu() 使用relu激活函数。

from torchvision import transforms 是为了使用

transform = transforms.Compose([ ])

transforms.ToTensor()

原图像是28*28，PIL读取时转化成1*28(H x W x C)：H表示高，W表示宽，C表示通道。

把PIL.Image从 (H x W x C)形状转换为 (C x H x W) 的tensor。

同时把数据【0，255】转化到【0，1】

torchvision.transforms.ToTensor详解 | 使用transforms.ToTensor()出现用户警告 | 图像的H W C 代表什么_LolitaAnn的博客-CSDN博客_transforms.totensorhttps://blog.csdn.net/qq_36667170/article/details/1212227660.1307和0.3081是minist数据集的均值和标准差。

为什么需要转化到【0，1】？

因为神经网络的输入时【0，1】的时候，使用激活函数，进行反向传播之后的导数值会更大，有助于提高神经网络的效率。

一文读懂图像数据的标准化与归一化_·城府、的博客-CSDN博客_图像预处理为什么要归一化https://blog.csdn.net/qq_45704645/article/details/111089328

为什么需要输入均值和标准差？

就是根据均值和标准差来进行均值方差归一化的操作。

机器学习中的数据归一化、最值归一化、均值方差归一化（标准化）_iioSnail的博客-CSDN博客_均值方差归一化https://blog.csdn.net/zhaohongfei_358/article/details/117910661

transform = transforms.Compose([transforms.ToTensor(), transforms.Normalize((0.1307,), (0.3081,))])

import torch
from torchvision import transforms
from torchvision import datasets
from torch.utils.data import DataLoader
import torch.nn.functional as F
import torch.optim as optim

2.加载和处理测试集和数据集

需要对测试机进行打乱

train_dataset = datasets.MNIST(root='../dataset/mnist/', train=True, download=True, transform=transform)
train_loader = DataLoader(train_dataset, shuffle=True, batch_size=batch_size)
test_dataset = datasets.MNIST(root='../dataset/mnist/', train=False, download=True, transform=transform)

3.设计类Net继承Module,

使用Linear()进行线性变换；计算预测值y,最后一层不做激活。

为什么不做激活？

因为最后一层的激活在CrossEntropyLoss()里面，就是softmax()的操作。

class Net(torch.nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        #torch.nn.Linear(784, 512)为什么是784？
        #图像是1*28*28的。
        self.l1 = torch.nn.Linear(784, 512)
        self.l2 = torch.nn.Linear(512, 256)
        self.l3 = torch.nn.Linear(256, 128)
        self.l4 = torch.nn.Linear(128, 64)
        #因为数据集的是0-9的图像，所以输出是10维的
        self.l5 = torch.nn.Linear(64, 10)
 
    def forward(self, x):
        #把向量铺平
        x = x.view(-1, 784)  
        x = F.relu(self.l1(x))
        x = F.relu(self.l2(x))
        x = F.relu(self.l3(x))
        x = F.relu(self.l4(x))
        # 最后一层不做激活，不进行非线性变换
        return self.l5(x)  
 
 
model = Net()

4. 设置损失函数和激活函数

momentum表示冲量。

冲量有什么作用？

一般，神经网络在更新权值时，采用如下公式:

w = w - learning_rate * dw

引入momentum后，采用如下公式：

v = mu * v - learning_rate * dw

w = w + v

如果上次的momentum(v)与这次的负梯度方向是相同的，那这次下降的幅度就会加大，从而加速收敛。

深度学习中momentum参数的作用 - 赵立敏 - 博客园 (cnblogs.com)https://www.cnblogs.com/zhaolimin/p/15190568.html

# construct loss and optimizer
criterion = torch.nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.5)

5. 封装

训练：

代码和之前的分类问题差不多。但是这个数据集太大，所以加了几行代码：让每遍历300个minibatch输出一个平均损失。

测试：

_, predicted = torch.max(outputs.data, dim=1)

max()返回两个参数分别是预测值和维度。

由于输出是10维的行向量，所以dim=1，表示取每一行的最大值。

def train(epoch):
    running_loss = 0.0
    for batch_idx, data in enumerate(train_loader, 0):
        #获得一个批次的数据和标签
        inputs, target = data
        optimizer.zero_grad()
        #获得模型预测结果(64, 10)
        outputs = model(inputs)
        
        loss = criterion(outputs, target)
        loss.backward()
        optimizer.step()
        #进行平均损失的计算
        running_loss += loss.item()
        #每跑完300个batch,做一次记录
        if batch_idx % 300 == 299:
            #epoch+1, batch_idx+1
            #epoch in range(10)表示【0，10），所以加1
            #for batch_idx, data in enumerate(train_loader, 0)的索引值从0开始所以加1
            print('[%d, %5d] loss: %.3f' % (epoch+1, batch_idx+1, running_loss/300))
            running_loss = 0.0
 
#将测试封装 
def test():
    correct = 0
    total = 0
    with torch.no_grad():
        #for i,data in enumerate(train_loader,0):
            
            #x_data,y_data=data
        for data in test_loader:
            images, labels = data
            outputs = model(images)

            #dim = 1 表示输出所在行的最大值
            #dim = 0 表示输出所在列的最大值
            _, predicted = torch.max(outputs.data, dim=1)
            
            total += labels.size(0)

            ## 张量之间的比较运算
            correct += (predicted == labels).sum().item()
    print('accuracy on test set: %d %% ' % (100*correct/total))

运行结果

正确率最后大概保持在：97 %

[1,   300] loss: 2.240
[1,   600] loss: 0.931
[1,   900] loss: 0.420
accuracy on test set: 89 %
[2,   300] loss: 0.303
[2,   600] loss: 0.280
[2,   900] loss: 0.244
accuracy on test set: 92 %
[3,   300] loss: 0.195
[3,   600] loss: 0.175
[3,   900] loss: 0.161
accuracy on test set: 95 %
[4,   300] loss: 0.136
[4,   600] loss: 0.129
[4,   900] loss: 0.119
accuracy on test set: 96 %
[5,   300] loss: 0.100
[5,   600] loss: 0.098
[5,   900] loss: 0.099
accuracy on test set: 96 %
[6,   300] loss: 0.081
[6,   600] loss: 0.081
[6,   900] loss: 0.074
accuracy on test set: 97 %
[7,   300] loss: 0.060
[7,   600] loss: 0.065
[7,   900] loss: 0.064
accuracy on test set: 97 %
[8,   300] loss: 0.051
[8,   600] loss: 0.049
[8,   900] loss: 0.055
accuracy on test set: 97 %
[9,   300] loss: 0.040
[9,   600] loss: 0.042
[9,   900] loss: 0.042
accuracy on test set: 97 %
[10,   300] loss: 0.029
[10,   600] loss: 0.037
[10,   900] loss: 0.036
accuracy on test set: 97 %