分类、聚类模型

一、分类模型

（1）逻辑回归

直接使用原来的回归模型进行回归，这时的因变量y只能取0或者是1，这回存在内生性问题，这会造成估计出的回归系数不一致并且有偏：

对于一个线性回归方程:

在概率论与数理统计中，对于二值的事件存在一个两点分布（伯努利分布），映射到0-1的二值问题，同样可以将他们结合：

这里的F称作连接函数，它将解释变量X和被解释变量Y连接在一起，同样的考虑到二值分布和0-1因变量的取值限制，在数理统计中，两点分布的期望计算方式是：
两点分布的期望 = 1 * P（事件1的发生概率）+ 0 * P（事件0的发生概率 = 事件1的发生概率

通过两点分布的期望计算方式我们可以讲预测值y 理解为 y=1的发生概率。

所以对于连接函数我们只需要保证连接函数F是一个定义在[0,1]上的函数，即保证F函数的值域是在[0,1]上。

通过上述的分析连接函数可以有两种取法：一种是probit回归，另外一种是logistic回归。

对于上述两种回归，后者logsitic回归更为常用，所以后面仅记录logsitic的计算。

那么逻辑回归是如何求解的？
对于非线性模型，使用的是极大似然估计(MLE)进行估计：

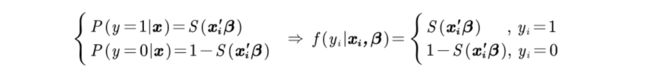
那么如何应用于分类？

我们计算出的的预测值就是事件1发生的概率（参考一下概率论中两点分布的思维~)，那么我们可以以0.5作为一个分界线，若事件1的计算值超过0.5，即事件1的发生概率超过0.5，那么我们认为这件事情发生了，若小于0.5我们认为这件事没有发生，就是事件2发生了。

（2）举个逻辑回归的例子–水果分类

预测成功率，我们将0看作是橙子，将1看作是苹果。

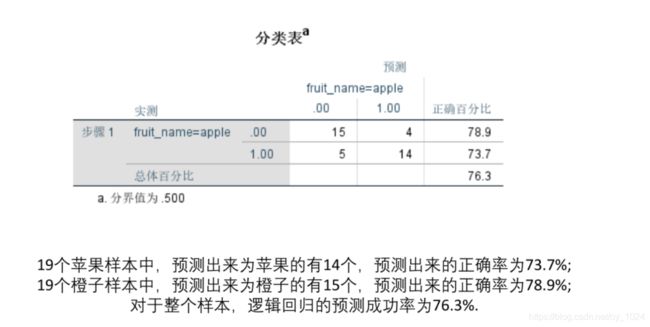
逻辑回归系数表，就是回归方程前的系数。

如果使用逻辑回归出的结果很差怎么办？
可以在logistic回归模型中添加平方项、交互项等，但是这回出现一个过拟合的问题，虽然使得回归模型能够以较高的准确率预测样本数据，但是对于新数据并不能很好的预测。

假设我们对上面的例子添加平方向后：、

我们添加平方项后，预测的准确率达到了100%，模型对于样本数据的预测非常好，但是对于样本外的数据预测效果可能会很差。结论就是添加高次或者是交互项后，虽然预测的能力提高了但是容易发生过拟合现象，这又再一次提醒在回归里不能随意的添加高次、交互项等，每一步操作必须有理有据。

那如何选择和确定合适的模型？
交叉验证：把数据分为训练组和测试组，使用训练组的数据来估计出模型，然后在使用测试组的数据进行测试，最终选择合适的模型。

那么对于上面的例子：

（为消除数据偶然性的影响，可以对上述步骤多重复几次，最终对每个模型求一个平均的准确率，这个步骤或者说这个思想称为交叉验证）

同样的逻辑回归也可以处理多分类的问题，只需将映射函数Sigmoid函数转化为Softmax函数

（3）Fisher线性判别分析

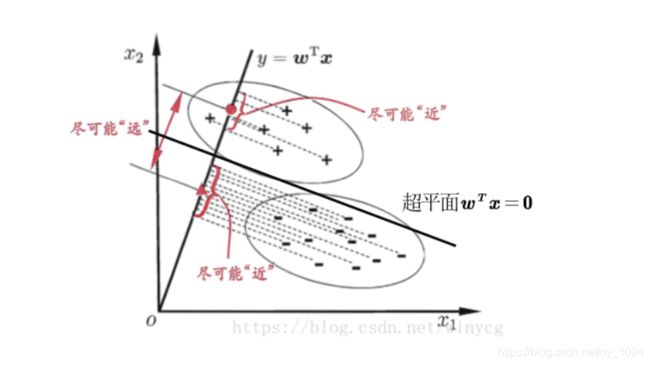
LDA是一种典型的线性判别方法，又称Fisher判别分析。该方法的思想是给定训练集样例，设法将样例投影到一维的直线上，使得同类样例的投影点尽可能的接近和密集，异类投影点尽可能的远离（换句话说就是将所有的一条线上，而这条线的法向量就是我们要寻找的超平面，并且这个平面所划分的点满足类内小、类间大的特点）

所以Fisher模型的核心问题就是找到线性系数向量W。

（4）举个Fisher线性判断的例子

还是上面的那个水果分类问题。我们使用Fisher线性判断对它进行分类。

点则判别函数系数表：就是我们所求的线性系数向量W

分类函数系数（贝叶斯判别函数系数表），就是将样品的各参数带入2各贝叶斯判别函数，比较得出函数值，那个函数值最大就将样品归到哪一类中。

两种系数，将每个数值代入计算，哪一类得到的数值大，就将其归为哪一类。

例如：

将第一行数据带入计算，第一列参数得到的值为0.23750，第二列参数得到的值为0.76250，所以我们将其归到第二列，就是判为1。

Fisher判别分析同样可用于多分类问题，只需将定义范围修改为因变量的种类个数即可，同时要注意的是此时的最小值只能为1

二、聚类模型

“物以类聚、人以群分“，聚类算法顾名思义就是将样本划分为有类似的对象组成的多个类的过程。聚类后可以更加准确的在每个类中单独使用统计模型进行估计、分析或者是预测，同时也可以探究不同类之间的相关性和主要差异。

聚类和上面的分类的区别就是：分类是已知类别的，而聚类是未知类别的

（1）K-means聚类算法

K-means聚类算法的流程：

1. 指定需要划分的簇的个数（就是K值，类的个数）
2. 随机的选择K个数据对象作为初始的聚类中心（不一定是我们要的样本点）
3. 计算其余的各个数据对象到这K个初始聚类中心的距离，把数据对象划归到距离它最近的那个中心所在的簇类中
4. 调整新类并且重新计算出新类的中心
5. 循环步骤三和步骤四，看中心是否收敛（不变），如果收敛或者达到迭代次数则停止循环
   

K-means算法的评价：
优点：

1. 算法简单、快速
2. 对处理大数据集，该算法是相对高效率的

缺点：

1. 算法要求用户必须事先给出要生成的簇的数目K
2. 对于初始值敏感（如果以开始我们设置的初始值点位置不恰当，比如说很靠近异值点、孤立点，会受到异值点的影响很大，求出的结果会不是很满意
3. 对于孤立的数据点敏感

（2）K-means++算法

k-means++ 算法选择初始值聚类中心的基本原则是：初始的聚类中心之间的相互距离要尽可能的远

算法的描述（对K-means算法”初始化K个聚类中心“进行了优化，就是在K-means++ 算法中不用再随机选取初始值）：

PS：举个例子


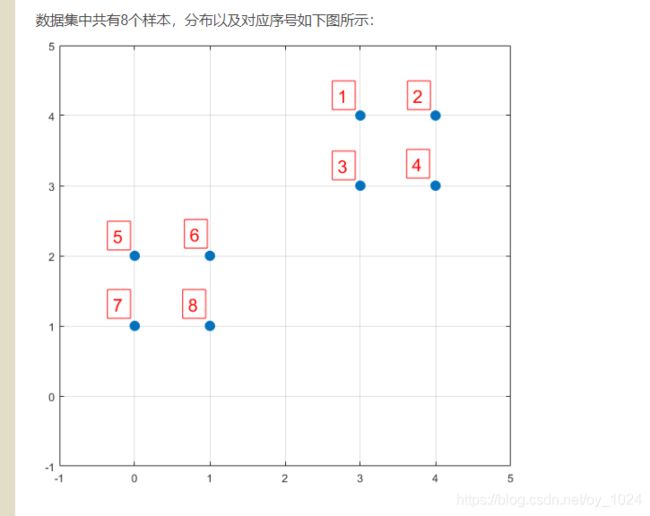
图片来源：https://www.cnblogs.com/wang2825/articles/8696830.html

（3）举个例子–K-means++聚类算法

对1999年全国31个省份居民家庭平均全年消费的的支出进行分类。分两类（K=2）

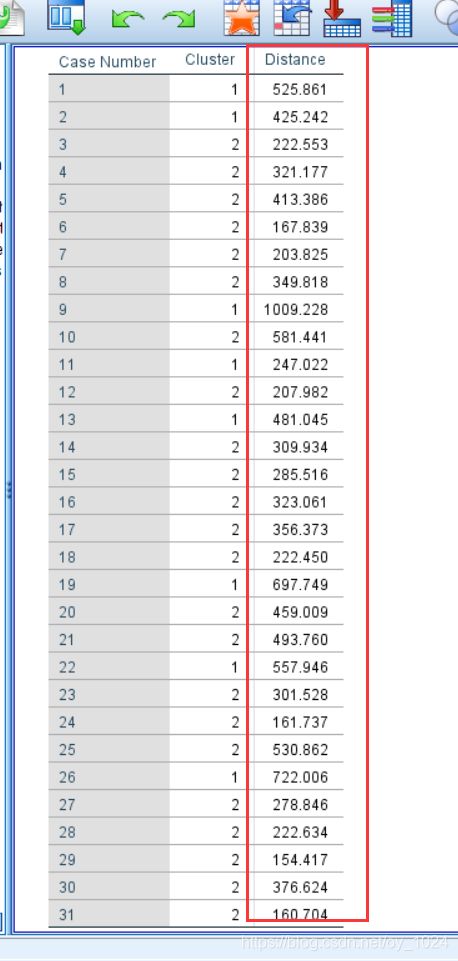
需要讨论的地方

• 聚类的K值怎么定：分几类主要是取决于个人的经验与感觉，通常的做法是多尝试几个K值，要看分成几类的结果更好解释、更符合分析的目的就分成几类。但是在比赛中更为常见的作法是参考一些论文，看看对于该类问题一般是可以分为几个方面的问题去解决。

• 数据量纲不一致怎么办：数据的量纲不一样得出的结果就没有什么意义，如果数据中存在不同的量纲，就需要将数据进行标准化。
  

对应的SPSS中的操作

（4）系统层次聚类

系统聚类的合并算法是通过计算两类数据点之间的距离，对最为接近的两类数据点进行组合，并反复迭代这一过程，直到将所有的数据点合成一类，生成聚类谱系图。

引例：



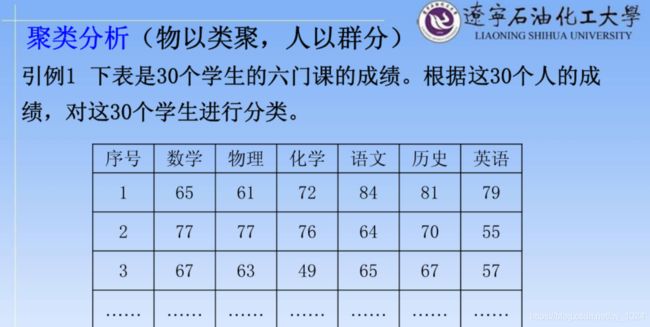
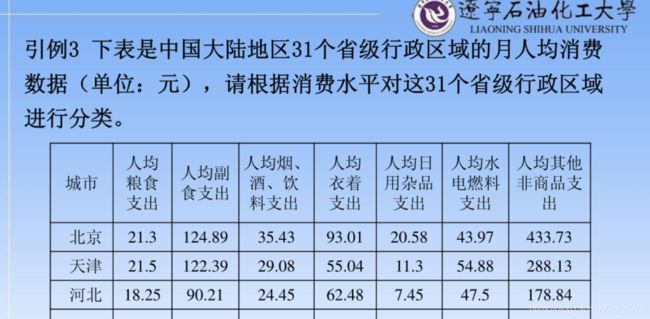
如何对数据进行分类？如果有两类数据生成的就是一个二维的坐标图。

分类的准则就是将距离近的样品聚为一类。

1、样品与样品之间常用的距离计算方法

举个例子对它进行计算： ID与ID之间

2、指标与指标常用的距离计算方法

举个例子说明一下计算过程

3、类与类之间常用的距离

最短距离法

最长距离法

组间平均连接法

组内平均连接法

重心法

4、最短距离系统聚类法

最短距离的操作方法，每次都选出最小距离，将这两类作为一个新类，并不断重复该步骤，最后得出聚类谱系图。

5、最长距离系统聚类法

同样是上面的例子，但是不同的是每次计算的是最大值，在每个类距离的最大值的得出的结果后，在再这些最大值中选择最小值将其合并。

6、聚类分析需要主意的问题

7、对系统聚类举个例子

还是上面的那个例子，得出谱系图，针对得出的谱系图我们可以选择自己想要的结果（就是K值）。

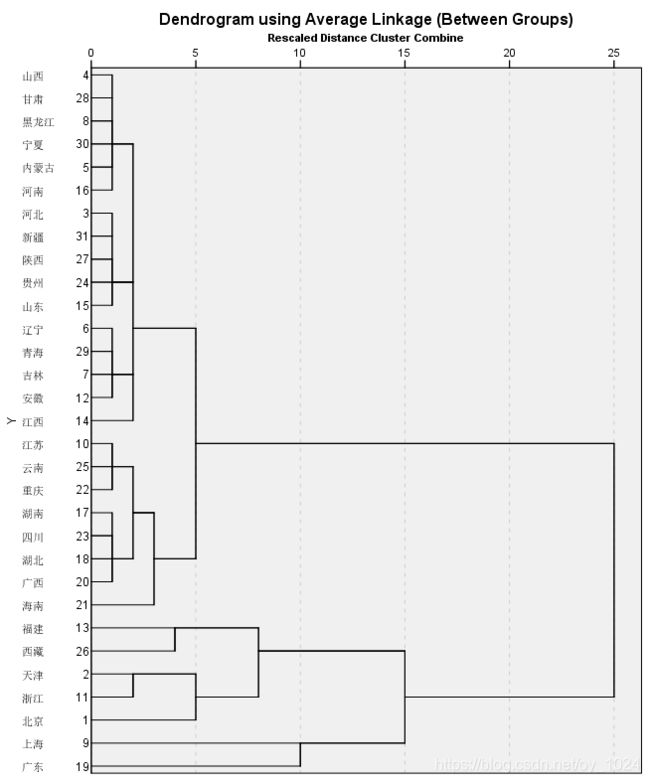
8、肘部法则–那怎么判断K值是合适的？

肘部法则是使用图形来估计聚类的数量

在得到的系数表中，可以获得各个聚合系数，以聚类的类别数K维横坐标，纵坐标为聚合系数画出聚合系数折线图。


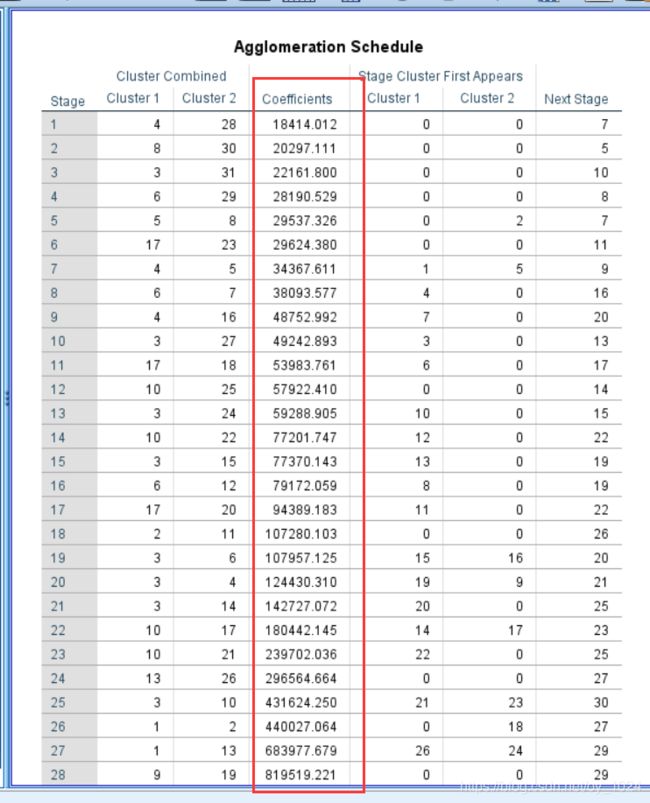
通过做出的聚合系数折线图，可以有下面的分析：

1. 当类别数（K值）为5时，折线图的下降去式趋缓，顾可以将类别的数目设定为5.
2. 从图中可以看出，K值在从1到5时，畸变程度变化最大，在超过5后，畸形程度变化显著降低，因此肘部就是K=5，所以可以将类别数设定为5。

在选出类别系数K后，就可以根据类别数得出分类结果，然后画出聚类结果图。

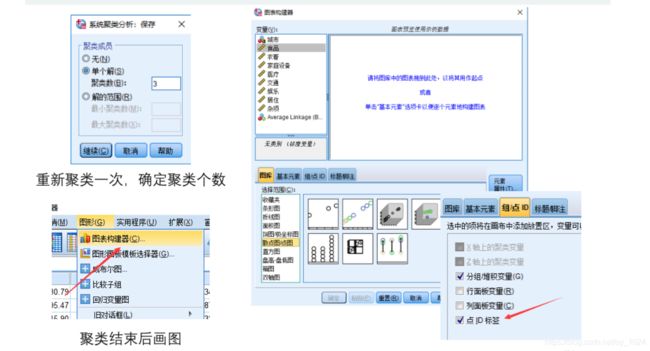
9、系统聚类法的流程

（3）DBSCAN密度聚类算法

DBSCAN算法是一种基于密度的聚类方法，聚类前不需要预先指定聚类的个数。DBSCAN算法利用基于密度的聚类概念，就是要求聚类空间中一定区域内所包含对象（点或者是其他空间对象）的数目不小于某一给定的阈值，该方法能在具有噪声的空间数据库中发现任意形状的簇，可将密度足够大的相邻区域连接，能够有效的处理异常数据。

DBSCAN的基本概念
B C是边界点 ，N是噪声点

DBSCAN算法的优缺点

聚类较好的情况

聚类较差的情况

DBSCAN聚类体验网站：https://www.naftaliharris.com/blog/visualizing-dbscan-clustering/

Matlab官网推荐下载的DBSCAN代码： https://ww2.mathworks.cn/matlabcentral/fileexchange/52905‐dbscan‐clustering‐algorithm

所以这个算法什么时候用？一般是只有两个指标，并且做出的散点图它的图形很明显的时候。