python的opencv操作记录(八)——小波变换
文章目录
- 什么是小波
-
- 从一个例子入手
- 把例子再深化一下
- 各种个样的小波基
-
- 哈尔小波
- 其他小波
- 小波分解
- 图像(二维)小波变换
什么是小波
上一篇里提到了stft,短时傅里叶变换,是针对不稳定信号进行加窗来做每一个小窗口的频谱分析。然后一个一个的时间窗就可以理解为时域。
在stft中,窗口的大小是固定的,太大无法分辨,太小又无法获得足够的信息(一个极端的例子就是一个窗口中只有一个信号采样点,那么就根本没有频率的概念了)
一种新的信号分析的方式就是小波变换,也有叫小波分解的,接下来久来讲一讲这个小波变换。
从一个例子入手
假设我们有一个恒定的信号,总共8个信号采样点:
signal = [1, 3, 5, 7, 9, 11, 13, 15]
如果要对这个信号中的信号点进行分析的话,可以采用下面一种分析方式:
- 计算每两个信号的平均值,那么这个信号就可以变成:[(1+3)/2=2, (5+7)/2=6, (9+11)/2=10, (13+15)/2=14],总共4个平均值。这样可以从某种程度上可以描述原信号的一些特征,这就可以称作是一种转换或者说分解,但是如果只有这样一种转换,转换后是无法恢复到原信号的,那么就还需要一点别的信息。
- 在上面的基础上,我们再计算每两个信号点之间的差,再除以二。经过这样的一个变换,我们又可以得到一组变换后的信号值:[(1-3)/2=-1, (5-7)/2=-1, (9-11)/2=-1, (13-15)/2=-1]
得到上面两组变换后,就可以将一个原始信号做一个变换或者说一种分解,而且还可以从这种变换逆变换回去。
把例子再深化一下
看一下小波变换的一般公式:公式一
α = W T f \alpha = W^Tf α=WTf
其中
- α \alpha α就是转换后的小波系数,分成尺度系数和细节系数,后面会具体提到这两个东西。
- f f f为原信号的函数
- W T W^T WT为转换矩阵
接着上面的例子,我们可以这么去理解:
α \alpha α就是由平均值和相减除2的值组成的向量:[2,6,10,14,-1,-1,-1,-1],那么,小波变换的一般公式就可以写成:
[ 2 6 10 14 − 1 − 1 − 1 − 1 ] = [ ] [ 1 3 5 7 9 11 13 15 ] \begin{bmatrix} 2 \\ 6 \\ 10 \\ 14 \\ -1 \\ -1 \\ -1 \\ -1 \end{bmatrix} = \begin{bmatrix} \\ \\ \\ \\ \\ \\ \\ \end{bmatrix} \begin{bmatrix} 1 \\ 3 \\ 5 \\ 7 \\ 9 \\ 11 \\ 13 \\ 15 \end{bmatrix} ⎣ ⎡261014−1−1−1−1⎦ ⎤=⎣ ⎡⎦ ⎤⎣ ⎡13579111315⎦ ⎤
中间空出来的部分就是我们需要去找到小波变换矩阵。
通过数据计算可以得到下面这样一个矩阵:

对于这个矩阵,有一个约束是要满足数学上的“规范正交化”,这个不是我这篇文章需要关心的内容,有兴趣的朋友可以自行去了解。
各种个样的小波基
回到小波函数的话题上来,如上面的公式一所列的,小波基可以理解为一个一个的这样的变换矩阵,可以把一个原始信号变换成另外一个向量,这个向量可以分成两个部分:
- 尺度部分(注意不是上面的求平均值,上面只是举个例子),好像也可以称之为高频部分
- 细节部分(注意也不是上面的两个数相减除二,同样上面只是举个例子),也可以称之为低频部分
哈尔小波
哈尔小波是最简单的一个小波基(变换形式),haar小波的变换矩阵如下:

我们使用python的一个小波变换库来验证一下这个过程:
import pywt
def demowavelets():
x = [1, 1, 1, 1, 1, 1, 1, 1]
dwt_haar = pywt.dwt(x, wavelet=pywt.Wavelet('haar'))
print(dwt_haar)
if __name__ == '__main__':
demowavelets()
dwt是表示用的离散小波变换,还有一个是连续小波变换,这个后面再详细说,先了解一下。
看一下输出是:
(array([1.41421356, 1.41421356, 1.41421356, 1.41421356]), array([0., 0., 0., 0.]))
这里是两个数组,分别是上面的尺度部分和细节部分。
当然恰好哈尔小波变换和我们的例子很类似:
- 尺度部分是两个数字相加再取根号,所以四个1.414
- 细节部分和例子中的结果碰巧是一样的,是四个0,换成别的就不一样了
有兴趣的朋友自己用矩阵计算的方式来计算一下。
这里有个问题是,如果不够变换的长度或者不满足要求的话,就会有一个补齐的动作,可以参考pywt官网的说明:
https://pywavelets.readthedocs.io/en/latest/ref/signal-extension-modes.html?highlight=padding#padding-using-pywavelets-signal-extension-modes-pad
默认是constant:
也就是根据最前或者最后的一个采样数据补充常量:
… x1 x1 | x1 x2 … xn | xn xn …
其他小波
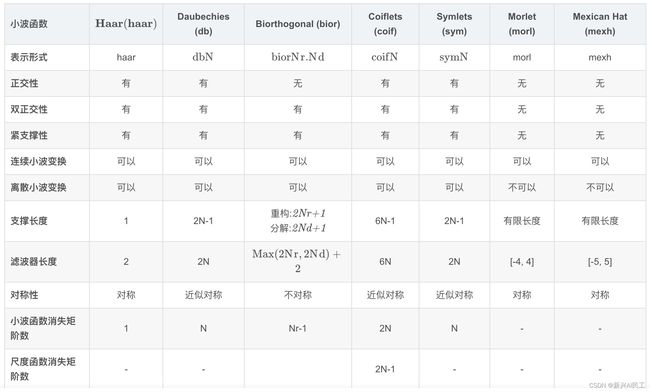
还有很多的小波种类,文章里就不一一列举了,我自己也没接触过几种,从网上搬了一个列表过来(侵删),有兴趣的朋友自行深入了解吧
也可以通过
print(pywt.families())
来输出pywt这个库支持哪些小波变换。
小波分解
小波分解的概念就是对其中一个部分进行不同层级的小波变换,一般来说是尺度部分。
可以理解上面提到的过程是就是第一层分解,对尺度部分再做一次小波变换,就可以叫做第二层,当然我们不需要自己去写循环进行分解,可以使用一个函数:
pywt.wavedec
dwt_one = pywt.wavedec(x, wavelet=pywt.Wavelet('haar'), level=2)
print(dwt_one)
输出就会变为:
[array([2., 2.]), array([0., 0.]), array([0., 0., 0., 0.])]
相当于对尺度部分做了两次变换,或者说分解。
当缩小到一个值的时候就不能再分解了,也就是这个信号的level最多只能是3
图像(二维)小波变换
图像是一个二维数据,我们对图像的行和列都做一下小波变换,就是2D小波变换了,这里存在一个顺序的问题,是先对行做还是先对列做的问题。
- 先把行分解到最精细,然后再分解列的方法叫做 standard decomposition
- 而行列交替分解的方法叫做 non-standard decomposition。
在pywt库中也提供了一个二维dwt的函数:
dwt2,这个函数的输出结果是

从物理含义上理解,第一象限从行的角度上来理解,是高频部分的数据,从列上来理解,也是高频部分的数据,所以是整张图像的高频部分。
然后,对于图像来说,高频一般出现在物体的边缘部分,想想看,只有像素值发生了较大的改变,这个东西才叫边缘。所以小波变换是提取物体边缘的一个很有用的工具。
一段demo,一般来说,变换后的图像是要做一些转换的,因为dwt之后的数字就不一定在0-255之间了。
img1 = np.zeros((100, 100, 3), dtype="uint8")
cv2.rectangle(img1, (60, 20), (70, 70), (255, 255, 255), 5)
cv2.rectangle(img1, (80, 20), (90, 70), (255, 255, 255), 5)
img1 = cv2.cvtColor(img1, cv2.COLOR_BGR2GRAY)
result = pywt.dwt2(img1, wavelet=pywt.Wavelet('haar'), mode='constant')
cv2.imshow("origin", img1)
img_dwt = result[0]
cv2.imshow("dwt", img_dwt)
cv2.waitKey(0)
cv2.destroyAllWindows()
- 第一象限的A表示一个“近似矩阵”
- 第二象限的V表示一个“垂直细节”
- 第三象限的H表示一个“水平细节”
- 第四象限的D表示一个“对角细节”
可以针对不同的需求取不同的数据进行处理和过滤,形成对特有图像的滤波器。

