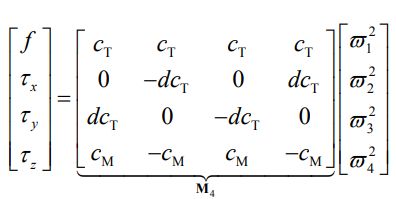多旋翼飞行器设计与控制（六）—— 动态模型和参数测量
多旋翼飞行器设计与控制（六）—— 动态模型和参数测量
一、多旋翼控制模型
- 刚体运动学模型。跟质量与受力无关，只研究位置、速度、姿态、角速度等参量，常以质点为模型。
- 刚体动力学模型。它与一般刚体动力学模型最大的不同是，拉力方向始终与机体轴zb轴的负方向一致。
- 控制效率模型。六旋翼和四旋翼的区别，就在这个控制效率模型上。
- 动力单元模型。以无刷直流电机、电调和螺旋桨为一组的整个动力机构。输入是0～1的电机油门指令，输出是螺旋桨转速。
多旋翼飞行控制刚体模型
1）基于欧拉角模型：
e p ′ = e v {^e}p \prime = {^e}v ep′=ev
Θ ′ = W ⋅ b ω \Theta \prime = W \cdot {^b} \omega Θ′=W⋅bω
2）基于旋转矩阵模型：
e p ′ = e v {^e}p \prime = {^e}v ep′=ev
R ′ = R [ b ω ] x R \prime = R [ {^b} \omega]_x R′=R[bω]x
3）基于四元数模型：
e p ′ = e v {^e}p \prime = {^e}v ep′=ev
q 0 ′ = − 1 2 q v T ⋅ b ω q_0 \prime = - \frac{1}{2} q^T_v \cdot {^b} \omega q0′=−21qvT⋅bω
q v ′ = 1 2 ( q 0 I 3 + [ q v ] x ) b ω q_v \prime = \frac{1}{2}(q_0 I_3+[q_v]_x) {^b} \omega qv′=21(q0I3+[qv]x)bω
4）地球系下的位置动力学模型：
e v ′ = g e 3 − f m e b 3 {^e} v \prime = g e_3 - \frac{f}{m} {^e} b_3 ev′=ge3−mfeb3
多旋翼只受重力和螺旋桨拉力，其中螺旋桨拉力沿着b系z轴负方向，重力沿着e系z轴正反向。
5）机体系下的位置动力学模型：
e v ′ = R ⋅ b v {^e} v \prime = R \cdot {^b} v ev′=R⋅bv
对上式两边求导可得：
e v ′ = R ⋅ b v ′ + R ′ ⋅ b v {^e}v \prime = R \cdot {^b}v \prime + R \prime \cdot {^b}v ev′=R⋅bv′+R′⋅bv
将旋转矩阵导数计算公式与地球系下的位置动力学模型代入上式可得：
b v ′ = − [ b ω ] × b v + g R T e 3 − f m e 3 {^b}v \prime = -[{^b}\omega ] \times {^b}v +g R^T e_3 - \frac{f}{m} e_3 bv′=−[bω]×bv+gRTe3−mfe3
6）姿态动力学模型：
J ⋅ b ω ′ = − b ω ⋅ ( J ⋅ b ω ) + G a + τ J \cdot {^b} \omega \prime = - {^b} \omega \cdot (J \cdot {^b} \omega) +G_a + \tau J⋅bω′=−bω⋅(J⋅bω)+Ga+τ
其 中 τ 表 示 螺 旋 桨 在 机 体 轴 上 产 生 的 力 矩 , G a 为 陀 螺 力 矩 ， J 为 转 动 惯 量 其中 \tau 表示螺旋桨在机体轴上产生的力矩 , G_a为陀螺力矩， J为转动惯量 其中τ表示螺旋桨在机体轴上产生的力矩,Ga为陀螺力矩，J为转动惯量
结合以上的姿态模型和分别用欧拉角、旋转矩阵、四元数表示的运动模型，可以总结如下三个综合的控制刚体模型：
控制效率模型
分析单个螺旋桨产生的拉力和力矩：
{ T i = c T ω i 2 M i = c M ω i 2 \left\{ \begin{array}{c} T_i = c_T \omega^2_i \\ M_i = c_M \omega^2_i \\ \end{array} \right. {Ti=cTωi2Mi=cMωi2
其 中 c T 和 c M 为 常 数 其中c_T 和 c_M 为常数 其中cT和cM为常数
由此我们可以得到标准四旋翼控制效率模型
1）标准四旋翼
作用在机体上的总拉力：
f = ∑ i = 0 4 T i = c T ( ω 1 2 + ω 2 2 + ω 3 2 + ω 4 2 ) f = \sum_{i=0}^4 T_i = c_T(\omega ^2_1 + \omega ^2_2 + \omega ^2_3 + \omega ^2_4) f=i=0∑4Ti=cT(ω12+ω22+ω32+ω42)
对于+字型四旋翼螺旋桨产生力矩为：
对于X字型四院系螺旋桨产生的力矩为：
综上，标准四旋翼中+字型的控制效率模型为：
标准四旋翼中x字型的控制效率模型为：
2）多旋翼
动力单元模型
二、多旋翼气动阻力模型
桨叶挥舞
桨叶挥舞是桨叶的上下运动。如上图（a）所示，前行桨叶逆风前进，因此获得更大的相对速度。这是作用在螺旋桨的拉力增大，产生向上挥舞速度。如上图（c），螺旋桨的向上挥舞速度会减小迎角，进而减小拉力。
如左图（a）所示，多旋翼向右飞行，螺旋桨逆时针旋转。在A点处产生最大的相对速度。然而，螺旋桨最大的上偏位置出现在B点，其中A点比B点滞后π/2。这个道理如同正弦曲线运动规律一般（如图（b））。因此，如图（
c）所示，螺旋桨桨盘下方是 前行螺旋桨区，上方是 后行螺旋桨区。因为位置滞后速度π/2，因此，前面半区是桨叶上偏区，而后面半区是桨叶下偏区。
由于螺旋桨的挥舞，改变了桨盘的方向，从而进一步改变了拉力的方向。从左图可以看出，拉力不再与多旋翼的机体轴zb轴平行，而是在xb轴负方向上产生分量，即诱导阻力。该阻力是多旋翼阻力的主要组成部分，不容忽视。多旋翼气动阻力模型将以此为依据。
气动阻力模型
三、多旋翼模型参数测量
测量重心位置
测量转动惯量
动力单元模型参数测量
电机——螺旋桨系统描述为：
ω = 1 T m s + 1 ( C R σ + ω b ) \omega = \frac{1}{T_ms+1} (C_R \sigma + \omega_b) ω=Tms+11(CRσ+ωb)
上 式 中 时 间 常 数 T m 为 动 态 参 数 ， C R 和 ω b 都 是 静 态 参 数 上式中时间常数T_m为动态参数，C_R和\omega_b都是静态参数 上式中时间常数Tm为动态参数，CR和ωb都是静态参数
不难发现上述系统是一个典型的一阶动态系统，输入为\sigma,输出为\omega,可以利用自控原理对系统进行分析
