gridsearchcv参数_使用Python进行超参数优化

可以在此处找到本文随附的代码。

https://github.com/NMZivkovic/ml_optimizers_pt3_hyperparameter_optimization

到目前为止，在学习机器学习的整个过程中，涵盖了几个大主题。研究了一些回归算法，分类算法和可用于两种类型问题的算法(SVM， 决策树和随机森林)。除此之外，将toes浸入无监督的学习中，了解了如何使用这种类型的学习进行聚类，并了解了几种聚类技术。在所有这些文章中，使用Python进行“从头开始”的实现和TensorFlow， Pytorch和SciKit Learn之类的库。

担心AI会接手您的工作吗？确保是构建它的人。与崛起的AI行业保持相关！

超参数是每个机器学习和深度学习算法的组成部分。与算法本身学习的标准机器学习参数(例如线性回归中的w和b或神经网络中的连接权重)不同，工程师在训练过程之前会设置超参数。它们是控制工程师完全定义的学习算法行为的外部因素。需要一些例子吗？

该学习速率是最著名的超参数之一，C在SVM也是超参数，决策树的最大深度是一个超参数等，这些可以手动由工程师进行设置。但是如果要运行多个测试，可能会很麻烦。那就是使用超参数优化的地方。这些技术的主要目标是找到给定机器学习算法的超参数，该超参数可提供在验证集上测得的最佳性能。在本教程中，探索了可以提供最佳超参数的几种技术。

数据集和先决条件

本文中使用的数据来自PalmerPenguins数据集。最近引入了此数据集，以替代著名的Iris数据集。它是由Kristen Gorman博士和南极洲帕尔默站创建的。可以在此处或通过Kaggle获取此数据集。该数据集实质上由两个数据集组成，每个数据集包含344个企鹅的数据。就像在鸢尾花数据集中一样，帕尔默群岛的3个岛屿中有3种不同的企鹅。同样，这些数据集包含每个物种的标本维度。高门是鸟嘴的上脊。在简化的企鹅数据中，顶点长度和深度被重命名为culmen_length_mm和culmen_depth_mm变量。

https://github.com/allisonhorst/palmerpenguins

由于该数据集已被标记，因此将能够验证实验结果。但是通常不是这种情况，并且对聚类算法结果的验证通常是一个困难而复杂的过程。

就本文而言，请确保已安装以下Python 库：

• NumPy  

• SciKit学习

• SciPy

• Sci-Kit优化

安装完成后，请确保已导入本教程中使用的所有必要模块。

import pandas as pdimport numpy as npimport matplotlib.pyplot as pltfrom sklearn.preprocessing import StandardScalerfrom sklearn.model_selection import train_test_splitfrom sklearn.metrics import accuracy_scorefrom sklearn.model_selection import GridSearchCV, RandomizedSearchCVfrom sklearn.svm import SVCfrom sklearn.ensemble import RandomForestRegressorfrom scipy import statsfrom skopt import BayesSearchCVfrom skopt.space import Real, Categorical

除此之外，至少要熟悉线性代数，微积分和概率的基础。

准备数据

加载并准备PalmerPenguins数据集。首先加载数据集，删除本文中未使用的功能：

data = pd.read_csv('./data/penguins_size.csv')data = data.dropna()data = data.drop(['sex', 'island', 'flipper_length_mm', 'body_mass_g'], axis=1)

然后分离输入数据并对其进行缩放：

X = data.drop(['species'], axis=1)ss = StandardScaler()X = ss.fit_transform(X)y = data['species']spicies = {'Adelie': 0, 'Chinstrap': 1, 'Gentoo': 2}y = [spicies[item] for item in y]y = np.array(y)

最后将数据分为训练和测试数据集：

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=33)

当绘制数据时，这里是它的样子：

网格搜索

手动超参数调整缓慢且令人讨厌。这就是为什么探索第一个也是最简单的超参数优化技术–网格搜索的原因。该技术正在加速该过程，它是最常用的超参数优化技术之一。本质上，它使试错过程自动化。对于这项技术，提供了所有超参数值的列表，并且该算法为每种可能的组合建立了一个模型，对其进行评估，然后选择能够提供最佳结果的值。这是一种通用技术，可以应用于任何模型。

在示例中，使用SVM算法进行分类。考虑了三个超参数C，gamma和kernel。要更详细地了解它们，请查看本文。对于C，要检查以下值：0.1、1、100、1000；对于gamma，使用值：0.0001、0.001、0.005、0.1、1、3、5；对于kernel，使用值：'linear'和'rbf'。这是代码中的样子：

hyperparameters = {    'C': [0.1, 1, 100, 1000],    'gamma': [0.0001, 0.001, 0.005, 0.1, 1, 3, 5],    'kernel': ('linear', 'rbf')}

利用Sci-Kit Learn及其SVC类，其中包含用于分类的SVM实现。除此之外，使用GridSearchCV 类，该类用于网格搜索优化。结合起来看起来像这样：

grid = GridSearchCV(        estimator=SVC(),        param_grid=hyperparameters,        cv=5,scoring='f1_micro',n_jobs=-1)

此类通过构造函数接收几个参数：

• 估计器–实例机器学习算法本身。在那里传递了SVC类的新实例。

• param_grid  –包含超参数字典。

• cv –确定交叉验证拆分策略。

• 评分–用于评估预测的验证指标。使用F1分数。

• n_jobs –表示要并行运行的作业数。值-1表示正在使用所有处理器。

剩下要做的唯一一件事就是通过使用fit方法来运行训练过程：

grid.fit(X_train, y_train)

训练完成后，可以检查最佳超参数和这些参数的分数：

print(f'Best parameters: {grid.best_params_}')print(f'Best score: {grid.best_score_}')Best parameters: {'C': 1000, 'gamma': 0.1, 'kernel': 'rbf'}Best score: 0.9626834381551361

同样，可以打印出所有结果：

print(f'All results: {grid.cv_results_}')

Allresults: {'mean_fit_time': array([0.00780015, 0.00280147, 0.00120015, 0.00219998, 0.0240006 ,

       0.00739942, 0.00059962, 0.00600033, 0.0009994 , 0.00279789,

       0.00099969, 0.00340114, 0.00059986, 0.00299864, 0.000597  ,

       0.00340023, 0.00119658, 0.00280094, 0.00060058, 0.00179944,

       0.00099964, 0.00079966, 0.00099916, 0.00100031, 0.00079999,

       0.002     , 0.00080023, 0.00220037, 0.00119958, 0.00160012,

       0.02939963, 0.00099955, 0.00119963, 0.00139995, 0.00100069,

       0.00100017, 0.00140052, 0.00119977, 0.00099974, 0.00180006,

       0.00100312, 0.00199976, 0.00220003, 0.00320096, 0.00240035,

       0.001999  , 0.00319982, 0.00199995, 0.00299931, 0.00199928,   

...

好的，现在建立这个模型，并检查它在测试数据集上的表现如何：

model = SVC(C=500, gamma = 0.1, kernel = 'rbf')model.fit(X_train, y_train)preditions = model.predict(X_test)print(f1_score(preditions, y_test, average='micro'))

0.9701492537313433

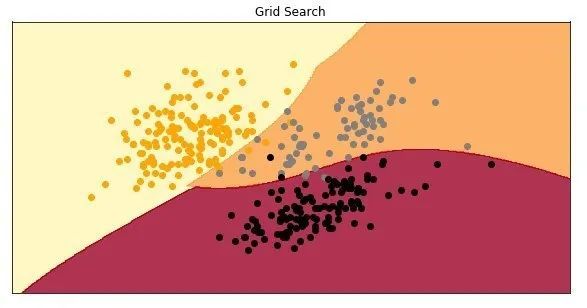
太酷了，使用建议的超参数的模型的准确度约为97％。这是绘制模型时的样子：

随机搜寻

网格搜索非常简单。但是它也计算昂贵。特别是在深度学习领域，训练可能会花费很多时间。同样，某些超参数可能比其他一些更重要。这就是为什么的想法随机搜索出生在引入本文。实际上，这项研究表明，就计算成本而言，对于超参数优化，随机搜索比网格搜索更有效。该技术还允许更精确地发现重要超参数的良好值。

就像Grid Search一样，Random Search会创建一个超参数值的网格，并选择随机组合来训练模型。这种方法有可能错过最佳组合，但是，与Grid Search相比，它出人意料地更频繁地选择了最佳结果，而且花费的时间很少。看看它在代码中如何工作。同样=使用Sci-Kit Learn的SVC类，但是这次使用RandomSearchCV 类进行随机搜索优化。

hyperparameters = {    "C": stats.uniform(500, 1500),    "gamma": stats.uniform(0, 1),    'kernel': ('linear', 'rbf')}random = RandomizedSearchCV(                estimator = SVC(),                param_distributions = hyperparameters,                n_iter = 100,                cv = 3,                random_state=42,                n_jobs = -1)random.fit(X_train, y_train)

请注意，对C和gamma使用了均匀分布。同样可以打印出结果：

print(f'Best parameters: {random.best_params_}')print(f'Best score: {random.best_score_}')

Best parameters: {'C': 510.5994578295761, 'gamma': 0.023062425041415757, 'kernel': 'linear'}

Best score: 0.9700374531835205

请注意接近但结果与使用Grid Search时不同。网格搜索的超参数C的值为500 ，而随机搜索的超参数C的值为510.59。仅此一项，就可以看到随机搜索的好处，因为不太可能将这个值放在网格搜索列表中。类似地，对于gamma来说，随机搜索得到0.23，而网格搜索得到0.1 。真正令人惊讶的是，Random Search选择了线性核而不是RBF，并且获得了更高的F1分数。要打印所有结果，使用cv_results_ 属性：

print(f'All results: {random.cv_results_}')

Allresults: {'mean_fit_time': array([0.00200065, 0.00233404, 0.00100454, 0.00233777, 0.00100009,

       0.00033339, 0.00099715, 0.00132942, 0.00099921, 0.00066725,

       0.00266568, 0.00233348, 0.00233301, 0.0006667 , 0.00233285,

       0.00100001, 0.00099993, 0.00033331, 0.00166742, 0.00233364,

       0.00199914, 0.00433286, 0.00399915, 0.00200049, 0.01033338,

       0.00100342, 0.0029997 , 0.00166655, 0.00166726, 0.00133403,

       0.00233293, 0.00133729, 0.00100009, 0.00066662, 0.00066646,

  ....

做与Grid Search相同的事情：使用建议的超参数创建模型，检查测试数据集的分数并绘制模型。

model = SVC(C=510.5994578295761, gamma = 0.023062425041415757, kernel = 'linear')model.fit(X_train, y_train)preditions = model.predict(X_test)print(f1_score(preditions, y_test, average='micro'))

0.9701492537313433

测试数据集上的F1分数与使用网格搜索时的分数完全相同。查看模型：

贝叶斯优化

关于前两种算法的一个非常酷的事实是，所有具有不同超参数值的实验都可以并行运行。这样可以节省很多时间。但是，这也是他们最大的不足。意思是，由于每个实验都是独立进行的，因此无法在当前实验中使用过去实验的信息。整个领域都致力于解决序列优化问题-基于序列模型的优化(SMBO)。在该领域中探索的算法使用先前的实验和对损失函数的观察。基于它们，尝试确定下一个最佳点。贝叶斯优化是这种算法之一。

就像来自SMBO组的其他算法一样，使用先前评估的点(在这种情况下，它们是超参数值，但我们可以概括)来计算损失函数的后验期望。该算法使用两个重要的数学概念-高斯过程和获取函数。由于高斯分布是在随机变量上完成的，因此高斯过程就是其对函数的推广。就像高斯分布具有均值和协方差一样，高斯过程由均值函数和协方差函数来描述。

采集函数是用于评估当前损耗值的函数。观察它的一种方法是将其作为损失函数。它是损失函数的后验分布的函数，描述了超参数的所有值的效用。最受欢迎的采集功能有望改善：

其中f是损失函数，x'是当前最佳超参数集。将所有这些放在一起时，Byesian优化是通过3个步骤完成的：

• 使用先前评估的损失函数点，使用高斯过程计算后验期望。

• 选择了最大化预期改进效果的新点集

• 计算新选定点的损失函数

将其引入代码的简便方法是使用Sci-Kit优化库，通常称为skopt。按照前面示例中使用的过程，可以执行以下操作：

hyperparameters = {    "C": Real(1e-6, 1e+6, prior='log-uniform'),    "gamma": Real(1e-6, 1e+1, prior='log-uniform'),    "kernel": Categorical(['linear', 'rbf']),}bayesian = BayesSearchCV(                estimator = SVC(),                search_spaces = hyperparameters,                n_iter = 100,                cv = 5,                random_state=42,                n_jobs = -1)bayesian.fit(X_train, y_train)

同样，为超参数集定义了字典。请注意使用了Sci-Kit Optimization库中的Real和Categorical类。然后以与使用GridSearchCV或RandomSearchCV相同的方式利用BayesSearchCV类。训练完成后，可以打印出最佳结果：

print(f'Best parameters: {bayesian.best_params_}')print(f'Best score: {bayesian.best_score_}')

Best parameters:

OrderedDict([('C', 3932.2516133086), ('gamma', 0.0011646737978730447), ('kernel', 'rbf')])

Best score: 0.9625468164794008

使用此优化，得到了截然不同的结果。损失要比使用随机搜索时高。甚至可以打印所有结果：

print(f'All results: {bayesian.cv_results_}')

All results: defaultdict(, {'split0_test_score': [0.9629629629629629,

  0.9444444444444444, 0.9444444444444444, 0.9444444444444444,  0.9444444444444444,

  0.9444444444444444, 0.9444444444444444, 0.9444444444444444, 0.46296296296296297,

  0.9444444444444444, 0.8703703703703703, 0.9444444444444444, 0.9444444444444444,

  0.9444444444444444, 0.9444444444444444, 0.9444444444444444, 0.9444444444444444,

  .....

具有这些超参数的模型在测试数据集上的表现如何？

model = SVC(C=3932.2516133086, gamma = 0.0011646737978730447, kernel = 'rbf')model.fit(X_train, y_train) preditions = model.predict(X_test)print(f1_score(preditions, y_test, average='micro'))

0.9850746268656716

这非常有趣。即使在验证数据集上得到的结果较差，在测试数据集上也得到了更好的分数。这是模型：

只是为了好玩，将所有这些模型放在一起：

备选方案

通常先前描述的方法是最流行和最常用的。但是如果以前的解决方案不适合，则可以考虑几种替代方法。其中之一是超参数值的基于梯度的优化。该技术计算有关超参数的梯度，然后使用梯度下降算法对其进行优化。这种方法的问题在于，要使梯度下降正常工作，需要凸且平滑的函数，而在谈论超参数时通常并非如此。另一种方法是使用进化算法进行优化。

结论

在本文中，介绍了几种众所周知的超参数优化和调整算法。了解了如何使用网格搜索，随机搜索和贝叶斯优化来获取超参数的最佳值。还看到了如何在代码中利用Sci-Kit Learn类和方法来实现。

推荐阅读

Hinton最新访谈：GPT-3效果不错，但和人脑比参数量仍少1000倍